Solving for time | One-dimensional motion | Physics | Khan Academy

Khan Academy
11 Jun 201109:35
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concepts of displacement, velocity, and time in the context of motion. It explains the difference between scalar (speed) and vector (velocity) quantities, emphasizing the importance of direction in velocity. The script then walks through the calculation of time taken for an object, in this case, Ben, to travel a distance of 720 meters at a constant velocity of 3 meters per second to the east. It illustrates how to solve for time using both scalar (distance and speed) and vector (displacement and velocity) approaches, highlighting the algebraic manipulation of formulas and the use of conventions for vector quantities.

Takeaways
  • 📐 Velocity is a vector quantity that includes both magnitude (speed) and direction.
  • 🕒 Time can be calculated using the formula time = distance / velocity.
  • 🏃 Ben is running at a constant velocity of 3 meters per second to the east, which is a vector description of his motion.
  • 🔄 When solving problems, it's important to consider the vector or scalar nature of the quantities involved.
  • 🤹‍♂️ Manipulating the basic formula of rate (speed) = distance / time allows us to solve for different variables.
  • 📐 Displacement is the vector equivalent of distance, taking into account the direction of movement.
  • 📝 In physics, conventions are used to define positive and negative directions for vector quantities.
  • 🌐 The concept of displacement is crucial when dealing with motion in one dimension, and it can be positive or negative based on the chosen convention.
  • 🧠 Understanding the algebraic manipulation of formulas is more valuable than memorizing them.
  • 🕵️‍♂️ The script emphasizes the importance of clarity in describing vector quantities, such as specifying 'to the east'.
  • 🔢 The calculation for time in the given scenario is 240 seconds, using either scalar or vector approach with the provided velocity and distance.
Q & A

  • What is the difference between speed and velocity?

    -Speed is a scalar quantity that only considers the magnitude of how fast an object is moving, while velocity is a vector quantity that includes both the magnitude (speed) and the direction of the object's motion.

  • Why is it important to distinguish between distance and displacement?

    -Distance is the total length of the path traveled by an object, while displacement refers to the change in position of the object, including both magnitude and direction. Understanding the difference helps in accurately analyzing motion, especially when the path is not straight.

  • If Ben is running east at a constant velocity of 3 meters per second, how can we calculate the time it takes for him to travel 720 meters?

    -We can use the formula for time, which is the distance divided by the rate (or velocity). So, time (t) = distance (720 meters) / velocity (3 m/s). Solving this gives t = 720 / 3 = 240 seconds.

  • What is the significance of using vector notation in physics problems?

    -Vector notation is important because it provides a way to accurately represent the direction of physical quantities, which is crucial for solving problems involving motion, forces, and other vector quantities that have both magnitude and direction.

  • How can we express the relationship between rate, distance, and time algebraically?

    -The relationship can be expressed with the formula: rate = distance / time. To find the time, we can rearrange the formula to time = distance / rate.

  • What is the convention for representing displacement in physics problems?

    -Displacement is typically represented by the symbol 's' to differentiate it from other variables, such as 'd', which is often used for the derivative operator in calculus.

  • How does the concept of positive and negative direction affect the interpretation of vector quantities?

    -Assigning positive and negative values to directions allows us to quantify the direction of motion or force along a chosen axis. For example, positive might mean eastward and negative might mean westward, which helps in performing calculations and interpreting results more effectively.

  • What is the unit of time we get when dividing meters by meters per second?

    -When dividing meters by meters per second, the meters in the numerator and denominator cancel out, leaving us with the unit of seconds for time.

  • How can we relate velocity and displacement in the context of the given problem?

    -In the context of the problem, velocity is the rate of displacement per time. So, if the displacement is 720 meters and the velocity is 3 meters per second, the time taken can be calculated as time = displacement / velocity.

  • What is the role of algebraic manipulation in solving physics problems?

    -Algebraic manipulation is crucial in physics as it allows us to rearrange and solve equations to find unknown quantities. It helps us to derive different forms of the same fundamental relationships, such as rate, distance, and time.

  • Why should we not memorize physics formulas?

    -We should not memorize physics formulas because they are essentially algebraic manipulations of each other, derived from basic principles. Understanding the underlying concepts allows us to manipulate and use these formulas flexibly to solve a variety of problems.

Outlines
00:00
🏃 Velocity and Time Calculation

This paragraph discusses the calculation of time based on velocity and distance. It begins with a scenario where Ben is running eastward at a constant velocity of 3 meters per second. The distinction between speed and velocity is clarified, emphasizing the importance of direction in defining velocity as a vector quantity. The problem of determining the time taken to travel a distance of 720 meters is solved using the formula for rate (velocity without direction), which is distance divided by time. The process involves algebraic manipulation to isolate time, resulting in a solution of 240 seconds. The paragraph also encourages understanding the underlying algebraic relationships rather than memorizing formulas, and highlights the common-sense approach to deriving them.

05:00
📐 Vector Analysis in Motion

The second paragraph delves into the vector nature of velocity and displacement. It introduces the concept of using a convention to define positive and negative directions, such as east being positive and west being negative. The problem of calculating time is approached again, but this time considering velocity as a vector quantity. The formula for displacement, which is velocity times time, is used to find the time taken for a displacement of 720 meters to the east. The solution process mirrors the scalar case but with the inclusion of directional notation. The paragraph concludes with a teaser for future discussions on multidimensional vector quantities and the importance of defining conventions for positive and negative directions in one-dimensional problems.

Mindmap
Keywords
💡displacement
Displacement refers to the change in position of an object and is a vector quantity, meaning it has both magnitude and direction. In the video, it is used to describe the distance Ben travels to the east, emphasizing the direction as well as the magnitude of the movement. The example given is calculating the time it takes for Ben to travel 720 meters to the east at a constant velocity.
💡velocity
Velocity is a physical quantity that describes the rate of change of an object's position with respect to time, and it includes both speed and direction. In the video, velocity is used to determine how fast and in which direction Ben is running. The concept is important for understanding the vector nature of motion, as it contrasts with speed, which is a scalar quantity and does not include direction.
💡constant velocity
Constant velocity implies that an object moves at a steady pace without any change in speed or direction. In the context of the video, Ben is running at a constant velocity of 3 meters per second to the east, which means he maintains the same speed and direction throughout his run.
💡time
Time is a fundamental concept in physics that refers to the continuous progression of events from the past through the present to the future. In the video, time is the variable that needs to be calculated based on the given displacement and constant velocity.
💡scalar quantity
A scalar quantity is a simple numerical value that represents only magnitude and does not include direction. In the video, speed is an example of a scalar quantity, as it only tells us how fast something is moving without any information about the direction of motion.
💡vector quantity
A vector quantity has both magnitude and direction, making it a more comprehensive description of a physical quantity than a scalar. In the video, displacement and velocity are described as vector quantities because they provide information about how far and in what direction something moves.
💡rate
Rate, in the context of physics, refers to the speed at which something occurs or changes per unit of time. In the video, the rate is given as 3 meters per second, which describes the constant velocity at which Ben is running.
💡distance
Distance is a scalar quantity that represents the total length of the path traveled by an object, without regard to its direction. In the video, the distance is the total meters Ben runs, which is 720 meters.
💡algebraic manipulation
Algebraic manipulation refers to the process of rearranging and combining mathematical expressions to solve for unknown variables. In the video, algebraic manipulation is used to solve for time by rearranging the equation that relates distance, rate, and time.
💡units
Units are the standard quantities that measurements are expressed in. In physics, units are crucial for ensuring that calculations are dimensionally consistent. The video emphasizes the importance of units when performing calculations, such as ensuring that time is expressed in seconds and distance in meters.
💡positive and negative convention
The positive and negative convention is a set of rules used to assign directions or values a positive or negative sign based on a chosen coordinate system or reference frame. In the video, it is suggested that such a convention could be used in more complex problems to distinguish between directions like east and west.
Highlights

The concept of velocity as a vector quantity, which includes both magnitude and direction, is introduced.

The distinction between speed and velocity is clarified, with speed being the scalar quantity and velocity being vector due to its directional component.

The problem of calculating time taken for Ben running at a constant velocity is presented, with a focus on the vector aspect of displacement.

The algebraic manipulation of the formula for rate or speed (distance divided by time) to find time when distance and rate are known is demonstrated.

The concept of rate or speed being equal to distance divided by time is reiterated, emphasizing the change in time.

The solution to the problem is shown by multiplying both sides of the equation by time to isolate the variable.

The importance of unit consistency in algebraic operations is highlighted, particularly when dealing with physical quantities.

The solution to the problem yields a time of 240 seconds for Ben to travel 720 meters at 3 meters per second.

The concept of memorizing formulas is discouraged in favor of understanding the underlying algebraic relationships.

The vector notation for velocity and displacement is introduced, with a focus on the directional aspect.

The convention of using 's' for displacement is explained, and the reason for avoiding 'd' is discussed in the context of calculus.

The vector version of the problem is solved by dividing displacement by velocity to find time.

The concept of positive and negative directions in one-dimensional problems is briefly introduced, hinting at future topics.

The practical application of the vector quantities and their mathematical treatment in physics problems is emphasized.

The potential for using different conventions for positive and negative directions in vector problems is discussed.

Transcripts

Browse More Related Video

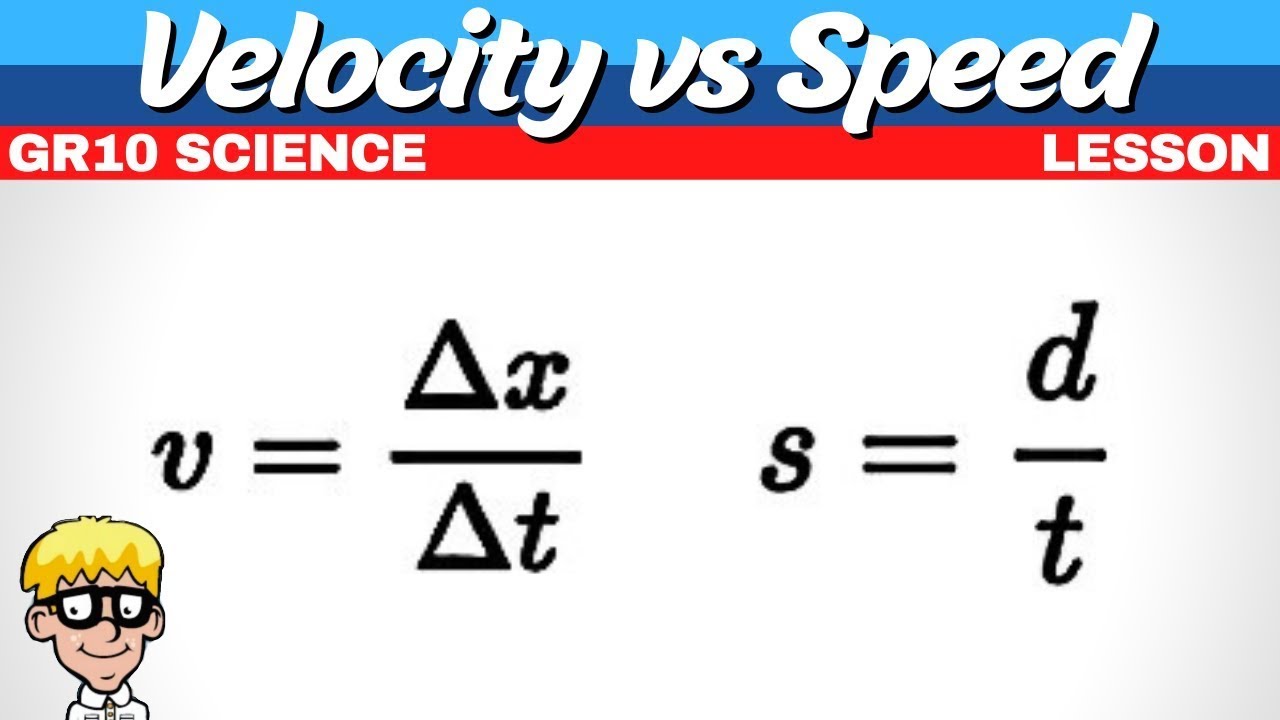
Velocity vs Speed Grade 10 Science

Displacement and Velocity - How is it different from Distance and Speed? | Physics

Kinematics In One Dimension - Physics

Intro to vectors & scalars | One-dimensional motion | Physics | Khan Academy

AP Physics 1 review of 1D motion

Calculating average velocity or speed | One-dimensional motion | Physics | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsMotion AnalysisVector QuantitiesScalar QuantitiesProblem SolvingEducational ContentAlgebraic ManipulationDirectional MovementTime Calculation