Kinematics in one dimension
TLDRThis transcript delves into the fundamentals of one-dimensional kinematics, exploring the concepts of position, displacement, average speed, average velocity, and acceleration. It distinguishes between scalar and vector quantities, emphasizing the importance of direction in vector calculations. The lecture introduces the equations of kinematics for constant acceleration, illustrating how to solve problems involving motion, and concludes with a discussion on freefall, highlighting the impact of gravitational acceleration and air resistance on object motion.
Takeaways
- 📐 Kinematics and dynamics are two branches of mechanics; kinematics describes motion, while dynamics deals with forces' effects on motion.
- 🎯 The position of an object in one-dimensional space is defined by a position vector, which has its tail at the origin and its head at the object's location.
- 🚗 Displacement is the straight-line distance between an object's initial and final positions and is a vector quantity indicating direction.
- 📈 Average speed is a scalar quantity calculated as the total distance traveled divided by the time taken, without regard to direction.
- 🏃 Average velocity is a vector quantity calculated as displacement divided by time, providing both magnitude and direction of motion.
- 📊 The graphical representation of average velocity is the slope of the position-time curve, which can be used to analyze motion.
- 🚀 Instantaneous velocity can be thought of as the limit of average velocity as the time interval approaches zero; it requires calculus for precise calculation.
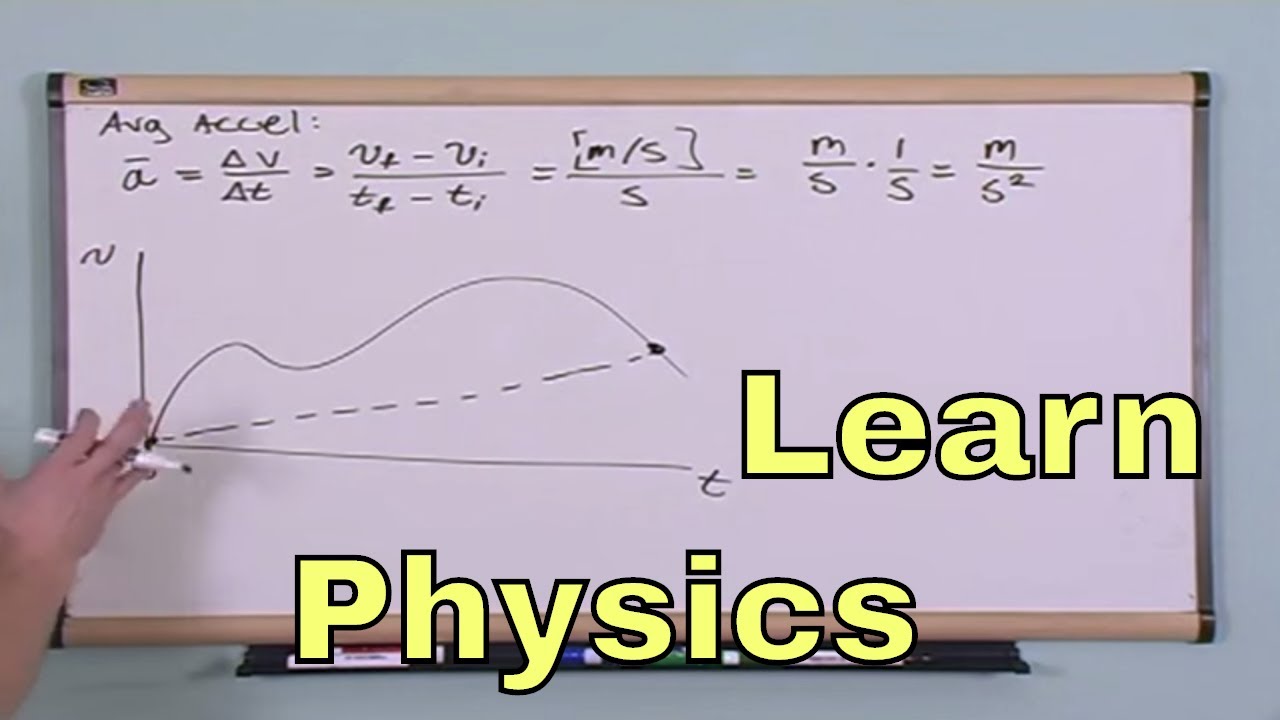
- 🌪 Acceleration is the rate of change of velocity with time and is a vector quantity, indicating how quickly an object speeds up or slows down.
- 📌 The equations of kinematics relate displacement, velocity, acceleration, and time for constant acceleration motion, allowing calculation of unknown quantities.
- 🛫 Freefall is a special case of motion with constant acceleration due to gravity, where objects fall towards the Earth without initial velocity.
- 📝 Solving kinematics problems involves identifying known quantities, selecting the appropriate equation, and applying constant acceleration principles to find the unknown variable.
- 🔄 When dealing with motion segments, the final velocity of one segment is the initial velocity of the next, which can be used to break down complex motion into simpler parts.
Q & A
What are the two branches of the science of moving objects?
-The two branches of the science of moving objects are kinematics, which deals with the concepts needed to describe motion, and dynamics, which deals with the effects that forces have on motion.
What is the definition of a position vector in one-dimensional reference frame?
-A position vector in a one-dimensional reference frame is a vector that has its tail at the origin and its head at the point of an object's location on the coordinate system. It is used to define the object's position in space.
How is displacement different from distance traveled?
-Displacement is the straight line distance between two positions during the motion of an object, while distance traveled is the actual length of the path taken by the object. Displacement and distance traveled are the same only when the motion is along a straight line.
What is the definition of average speed?
-Average speed is defined as the total distance traveled divided by the total time taken to cover that distance. It is a scalar quantity and does not provide information about the direction of motion.
How is average velocity different from average speed?
-Average velocity is a vector quantity that is defined as the displacement (change in position) divided by the time interval during which the displacement occurred. Unlike average speed, average velocity provides information about both the magnitude and direction of motion.
What is the definition of instantaneous velocity?
-Instantaneous velocity is the velocity of an object at a specific moment in time. It is the limit of the average velocity as the time interval approaches zero, essentially representing the slope of the tangent to the object's trajectory at that point.
How is acceleration defined and what are its units?
-Acceleration is defined as the rate of change of velocity with respect to time. It is calculated as the change in velocity (final velocity minus initial velocity) divided by the time interval over which the change occurred. The units of acceleration are meters per second squared (m/s^2) in the metric system.
What are the five kinematic variables and why are they important?
-The five kinematic variables are initial velocity (v0), final velocity (v), acceleration (a), displacement (x), and time (t). They are important because they allow us to describe and analyze the motion of an object with constant acceleration using a set of equations that relate these variables.
How do you apply the equations of kinematics to solve a problem?
-To apply the equations of kinematics, you first identify the known quantities and the desired unknown variable from the problem statement. Then, select the appropriate equation from the list of kinematic equations that relates the known quantities to the unknown variable, and solve for the unknown.
What is the significance of the minus sign in the equations of freefall?
-The minus sign in the equations of freefall signifies the direction of acceleration due to gravity, which is opposite to the positive orientation of the vertical axis (usually upward). It is crucial to include the minus sign when substituting the value of gravitational acceleration to ensure the correct calculation of the motion's outcome.
How does air resistance affect the motion of falling objects?
-Air resistance affects the motion of falling objects by slowing them down, especially if they have a large surface area or are not shaped to minimize drag. In a vacuum, all objects fall at the same rate regardless of their mass or shape, but in the presence of air resistance, lighter objects like a flat sheet of paper will fall slower than denser objects like a crumpled ball.
Why is it important to consider the direction when dealing with vector quantities in kinematics?
-It is important to consider the direction when dealing with vector quantities in kinematics because the direction provides essential information about the physical situation, such as the orientation of motion or the application of forces. Ignoring the direction can lead to incorrect results and misunderstanding of the motion's dynamics.
Outlines
📚 Introduction to Kinematics and Dynamics
This paragraph introduces the two branches of the science of moving objects: kinematics and dynamics. Kinematics deals with the concepts needed to describe motion, while dynamics focuses on the effects of forces on motion. Together, they form the branch of physics known as mechanics. The lecture primarily focuses on mechanics, discussing the position of an object in space, the introduction of a one-dimensional reference frame, and the concept of position vectors. It also explains how to use these vectors to define the position of a moving object at different times during its motion, with examples such as a car moving along a straight line and the definition of displacement.
📈 Understanding Displacement and Distance
This section delves deeper into the concepts of displacement and distance, emphasizing their differences and how they relate to the motion of objects. Displacement is defined as the straight-line distance between two positions and is a vector quantity, indicating direction as well as magnitude. Distance, on the other hand, is the total length of the path traveled and is a scalar quantity. The paragraph uses examples to illustrate how displacement and distance can differ, especially when the path of motion is not a straight line. It also introduces the concept of average speed, which is the distance traveled divided by the time taken, and explains that it is a scalar quantity without direction.
🌟 Calculation of Displacement with Signs
This part of the lecture focuses on the importance of signs in displacement calculations. The sign of a displacement vector indicates its direction relative to the chosen coordinate system. Positive displacement values indicate movement in the positive direction, while negative values indicate movement in the opposite direction. The paragraph provides examples of calculating displacement with proper sign considerations, highlighting the impact of the initial and final positions on the resulting displacement vector. It also introduces the concept of average velocity, which is a vector quantity that provides more information than average speed, including direction.
🕒 Graphical Representation of Average Velocity
This paragraph discusses the graphical representation of average velocity, which is the slope of the curve representing position versus time on a graph. By selecting two points along the trajectory of motion and calculating the displacement and the time interval between these points, one can determine the average velocity. The lecture explains that the graphical meaning of average velocity is the slope of the curve between two points, and it provides an example of how to calculate average velocity for a jogger given the distance and time of the run.
🚗 Example Calculations of Average Velocity
This section presents example calculations of average velocity, using the scenario of a test driver attempting to set a world record for the fastest speed with a car. The driver makes two runs in opposite directions to account for wind effects, and the average velocity is calculated for each run, highlighting the significance of the minus sign in vector calculations. The paragraph emphasizes that while velocity as a physical quantity is always positive, the direction of motion is indicated by the sign of the velocity vector in the reference frame.
🔄 Instantaneous Velocity and Acceleration
This paragraph introduces the concept of instantaneous velocity, which is the velocity of an object at a specific point in its trajectory. It is calculated as the limit of the average velocity as the time interval approaches zero, essentially the slope of the tangent to the trajectory at that point. The lecture notes that instantaneous velocity requires knowledge of calculus, which is not covered in this course. The paragraph then transitions to the topic of acceleration, which describes the rate of change of velocity over time. The definition and calculation of average acceleration are provided, along with examples of positive and negative acceleration, emphasizing the vector nature of acceleration and the importance of direction indicated by the sign of the result.
📌 Kinematic Equations for Constant Acceleration
This section introduces the five kinematic variables essential for analyzing motion with constant acceleration: displacement, acceleration, final velocity, initial velocity, and time. The lecture presents the four kinematic equations that relate these variables, allowing the calculation of one quantity when the other three are known. These equations are crucial for solving problems involving the kinematics of motion. The paragraph also discusses the strategy for solving kinematics problems, including sketching the problem, identifying known and unknown variables, selecting the appropriate equation, and calculating the unknown quantity. The importance of considering the direction of motion when solving problems is reiterated.
🚤 Application of Kinematic Equations
This paragraph demonstrates the application of kinematic equations through examples involving a speed boat and an aircraft carrier. The examples show how to use the equations to calculate displacement and the length of the deck required for a jet to take off safely. The lecture emphasizes the importance of using the correct signs when substituting values into the equations and the need to consider the physical situation when interpreting the results, as some problems may have two possible solutions.
🌐 Freefall Motion and Its Equations
This section discusses freefall motion, which occurs when an object is released from rest and falls under the influence of gravity. The kinematic equations for freefall are presented in two different notations: one using the symbol 'a' for acceleration and another using 'G' for gravitational acceleration. The equations account for the constant acceleration due to gravity, which is directed vertically downward. The lecture provides an example of a stone falling from a tall building, illustrating how to use the equations to calculate the displacement and final velocity of the object after a given time of freefall.
🎓 Conclusion of One-Dimensional Kinematics
The lecture concludes with a recap of the importance of understanding the definitions of kinematic quantities for describing the motion of objects. It emphasizes that the concepts learned in this lecture can be expanded to more than one dimension, which will be covered in the next lecture. The summary reinforces the significance of the kinematic equations and the need to accurately account for the direction of motion when solving problems involving the motion of objects.
Mindmap
Keywords
💡Kinematics
💡One-dimensional reference frame
💡Position vector
💡Displacement
💡Average speed
💡Average velocity
💡Instantaneous velocity
💡Acceleration
💡Kinematic equations
💡Freefall
Highlights
The science of moving objects is divided into two branches: kinematics and dynamics.
Kinematics deals with the concepts needed to describe motion, while dynamics deals with the effects of forces on motion.
Mechanics is a branch of physics that combines kinematics and dynamics.
A one-dimensional reference frame is a straight line with positive orientation to the right and negative to the left, with an origin labeled as O.
The position of an object in a one-dimensional coordinate system is defined by a position vector.
Displacement is the straight-line distance between two positions during an object's motion and is different from distance traveled.
Average speed is a scalar quantity defined as the distance traveled divided by the time taken, with units in meters per second.
Average velocity is a vector quantity that gives both magnitude and direction, calculated as displacement divided by time.
Instantaneous velocity can be found by taking the limit of the average velocity as the time interval approaches zero.
Acceleration is the rate of change of velocity with time and is a vector quantity with units of meters per second squared.
Kinematic equations with constant acceleration allow us to solve for displacement, velocity, and time given certain initial conditions.
Freefall is a type of motion with constant acceleration due to gravity, ignored air resistance, and is simplified for problems close to the Earth's surface.
The acceleration due to gravity has a constant value of 9.8 meters per second squared in the metric system.
When solving kinematics problems, it's crucial to use the correct signs for vector quantities to ensure accurate results.
The five kinematic variables (displacement, acceleration, final velocity, initial velocity, and time) are essential for solving motion problems with constant acceleration.
In problems involving freefall, the standard positive direction is vertically up and the negative direction is vertically down.
For kinematic problems, there may be two possible answers, and it's important to determine which one makes physical sense.
When dealing with freefall motion, the kinematic equations need to account for the direction of gravitational acceleration.
The two versions of kinematic equations for freefall can be used interchangeably, with one requiring a minus sign for acceleration and the other using a positive value for gravitational acceleration.
In this course, air resistance is ignored for simplicity, and only the acceleration due to gravity is considered in freefall problems.
The basic strategy for solving kinematics problems involves sketching the problem, identifying known and unknown variables, selecting the appropriate equation, and solving for the desired outcome.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: