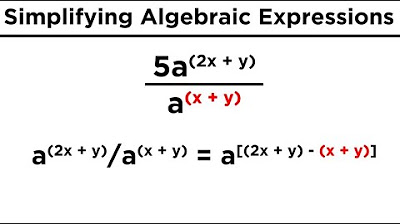Ch. 1.2 Exponents and Radicals
TLDRThis educational video script covers the fundamentals of exponents and radicals in the context of real numbers. It explains the rules of exponents, including multiplication, division, and raising to a power, and distinguishes between negative exponents and the opposite value of a quantity raised to a power. The script also delves into simplifying exponential expressions and introduces scientific notation for handling very large or small numbers. Furthermore, it explores the relationship between radicals and exponents, providing methods to simplify radicals by considering them as division problems and emphasizes the importance of rationalizing denominators to facilitate algebraic operations.
Takeaways
- 📝 Take clear and detailed notes while watching the video series, as it covers important concepts of exponents and radicals with real numbers.
- 🔢 Understand the basic definition of exponents: a number 'a' raised to the power 'n' means multiplying 'a' by itself 'n' times.
- 📌 Remember the difference between 'a to the n' and 'negative a to the n': the former signifies the base 'a' multiplied by itself 'n' times, while the latter involves calculating 'a to the n' first and then applying the negative sign.
- ⚠️ Be cautious with the rules of exponents, especially the distinction between 'negative a to the n' and 'a to the negative n', which can lead to opposite values depending on whether 'n' is even or odd.
- 📚 Learn the laws of exponents, which include multiplication and division of exponents, raising a power to a power, and the distribution of exponents over multiplication.
- 🔑 Utilize the arithmetic rules of exponents to simplify expressions involving multiple bases and exponents, making calculations more manageable.
- 📘 Apply the rules of exponents to scientific notation for handling very large or very small numbers in a compact form.
- 🤔 Grasp the relationship between exponents and radicals, recognizing that radicals can be expressed as fractional exponents and vice versa.
- 👉 Practice simplifying radical expressions by considering them as division problems, focusing on the quotient and remainder to simplify the expression under the radical sign.
- 📑 Use the process of rationalizing denominators to eliminate radicals from denominators in fractions, making the math more straightforward and understandable.
- 📈 Recognize the importance of simplifying complex expressions involving exponents and radicals, as it makes further mathematical manipulation and problem-solving more efficient.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is exponents and radicals, specifically as they pertain to real numbers.
What is the significance of the base 'a' and the exponent 'n' in the expression a^n?
-In the expression a^n, 'a' is the base, which is the number being multiplied by itself, and 'n' is the exponent, which tells us how many times the base is multiplied by itself.
What is the difference between a negative exponent and a negative base raised to a positive exponent?
-A negative exponent indicates the reciprocal of the base raised to the corresponding positive exponent. A negative base raised to a positive exponent results in a negative value only if the exponent is odd. The two can have the same value if the exponent is even, but they are conceptually different.
What are the rules of exponents discussed in the video?
-The rules of exponents discussed include a^0 = 1, a^(-n) as the multiplicative inverse of a^n, a^n * a^m = a^(n+m), a^n / a^m = a^(n-m), (a^n)^m = a^(n*m), a * b^n = a^n * b^n, and (a/b)^n = a^n / b^n.
How does the video script simplify the expression a^(m/n)?
-The expression a^(m/n) is simplified by using the rules of exponents to rewrite it as (a^m)^(1/n), which then can be interpreted as the mth root of a raised to the nth power.
What is the importance of scientific notation in mathematics?
-Scientific notation is important in mathematics for writing very large or very small numbers in a compact manner, making calculations and comprehension easier.
How does the script explain the relationship between exponents and radicals?
-The script explains that exponents and radicals are two sides of the same coin. Radicals can be written as exponential terms, specifically as a^(1/n), showing that they are essentially the same mathematical concept.
What is the process for simplifying radical expressions mentioned in the script?
-The process for simplifying radical expressions involves dividing the exponents by the root index, finding the quotient and the remainder, and then simplifying the expression by pulling out the whole number powers and leaving the remainder inside the radical.
What is the purpose of rationalizing the denominator in the script?
-Rationalizing the denominator is done to eliminate radicals from the denominator, making it easier to understand and perform algebraic operations on the expression.
Can you provide an example of rationalizing a denominator from the script?
-An example from the script is rationalizing the denominator of an expression like 3xy^2 / ∛(9xy^5) by multiplying both the numerator and the denominator by the cube root of the remaining terms to eliminate the radical from the denominator.
Outlines
📚 Introduction to Exponents and Radicals
This paragraph introduces the topic of exponents and radicals in the context of real numbers. The instructor emphasizes the importance of note-taking and engaging with the material through video pauses and rewinds. The basic definition of exponentiation is given, explaining how the exponent indicates the number of times the base is multiplied by itself. The difference between a number to the power of n and the opposite of that number raised to the power of n is clarified, highlighting the distinction between negative bases and the base being negative. The laws of exponents are introduced as a precursor to more complex arithmetic with exponents.
🔢 Laws of Exponents and Arithmetic Rules
The paragraph delves into the laws of exponents, which are essential for simplifying exponential expressions. It covers the properties of exponents when multiplying and dividing with the same base, raising a power to another power, and dealing with different bases. The instructor provides a mnemonic device for remembering these laws by relating them to the order of operations (PEMDAS). The explanation includes how to handle negative exponents and how they affect the position of terms in a fraction. The paragraph also discusses the distribution rule and its application in exponential expressions.
📝 Simplifying Exponential Expressions
This section focuses on applying the laws of exponents to simplify complex expressions involving multiple bases. The instructor provides a step-by-step method for simplifying, emphasizing the importance of keeping exponents positive and using arithmetic to find the final simplified form. The process involves combining like terms and applying the exponent rules to each base individually. The paragraph also discusses the concept of scientific notation and its use in handling very large or very small numbers in a compact form.
🔍 Advanced Simplification Techniques
The paragraph introduces advanced techniques for simplifying expressions with exponents, including the use of scientific notation for very large or small numbers. It explains the process of converting numbers into a form that can be easily multiplied or divided, using base 10 and its exponents. The instructor also discusses the concept of radicals as a part of exponentiation, showing how roots can be expressed as fractional exponents and vice versa. The importance of understanding the relationship between exponents and radicals for simplifying complex expressions is highlighted.
🌐 Understanding Radicals and Their Properties
This paragraph explores the properties of radicals, explaining how they are essentially exponents with fractional powers. The rules for simplifying radicals are discussed, including the division of exponents and the importance of the quotient and remainder in simplifying radical expressions. The instructor provides examples of how to simplify radicals by considering the division of exponents and the remainder that cannot be simplified further. The concept of rationalizing denominators is introduced as a necessary step for simplifying expressions involving radicals.
📉 Simplifying Complex Radical Expressions
The paragraph provides a detailed example of simplifying a complex radical expression by breaking it down into its components and applying the rules of exponents and radicals. The process involves converting the expression into fractional exponents, simplifying the exponents, and then converting back to radical form if necessary. The instructor emphasizes the importance of simplifying constants and variables separately and combining like terms to arrive at the final simplified expression.
📌 Rationalizing Denominators
This section discusses the concept of rationalizing denominators, which is the process of eliminating radicals from the denominator of a fraction. The instructor explains the importance of this process for simplifying algebraic expressions and making them easier to work with. Two cases are presented: when the denominator contains an nth root and when it contains a radical plus or minus another term. The method involves multiplying the numerator and denominator by an appropriate term to eliminate the radical, using either an nth root term or the radical conjugate.
🔄 Final Thoughts on Exponents and Radicals
In the concluding paragraph, the instructor summarizes the discussion on exponents and radicals, highlighting the importance of understanding these concepts in pre-calculus. The instructor also provides an overview of the next section and acknowledges the length of the current video, promising that future videos will vary in length. The goal is to ensure that students have a solid foundation in these fundamental topics before moving on to more advanced material.
Mindmap
Keywords
💡Exponents
💡Radicals
💡Base
💡Law of Exponents
💡Scientific Notation
💡Negative Exponents
💡Rationalizing Denominators
💡Roots
💡Fractional Exponents
💡Simplification
Highlights
Introduction to exponents and radicals in the context of real numbers.
The importance of note-taking and utilizing video features like pause, fast forward, and reverse for effective learning.
Explanation of the basic concept of exponentiation, emphasizing the meaning of base and exponent.
Clarification of the difference between negative exponents and the opposite value of a quantity raised to an exponent.
Introduction to the laws of exponents, which are essential for arithmetic operations on exponential expressions.
Detailed explanation of each law of exponents, including multiplication, division, and raising a power to a power.
The significance of distinguishing between 'a to the negative n' and 'negative a to the n' based on the parity of n.
A method for simplifying exponential expressions by applying arithmetic rules to individual bases separately.
The concept of scientific notation and its use for handling very large or very small numbers in a compact form.
The relationship between exponents and radicals, highlighting that radicals are a form of exponents.
Properties of radicals and how they can be rewritten as exponential terms, emphasizing the importance of n being even for real numbers.
Techniques for simplifying radical expressions by considering them as division problems and focusing on quotients and remainders.
The process of rationalizing denominators to eliminate radicals and make mathematical operations more straightforward.
Examples of rationalizing denominators using nth root terms and radical conjugates to simplify fractions.
The importance of simplifying complex expressions step by step to make them more manageable in mathematical problems.
Conclusion of the video with a summary of the topics covered and a preview of the next section.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: