Calculus 1 Lecture 2.5: Finding Derivatives of Trigonometric Functions
TLDRThe video script is an engaging lecture on calculus, focusing on the derivation of trigonometric functions. The instructor emphasizes the importance of understanding basic trigonometric identities and their derivatives, particularly for sine, cosine, tangent, secant, cosecant, and cotangent. The lecture includes a detailed walkthrough of deriving the slope of a tangent line using the derivative of a function, as well as practical examples like modeling the motion of a spring. The instructor also introduces the concept of higher-order derivatives and their cyclical nature, relating it to the oscillation of a spring. The script concludes with a teaser for the upcoming topic of the Chain Rule, a crucial method for handling complex derivatives.
Takeaways
- 📚 The class is focused on trigonometric functions and their derivatives, emphasizing the importance of understanding these for future math courses.
- 🔍 The instructor highlights six trigonometric functions: sine, cosine, tangent, secant, cosecant, and cotangent, and their derivatives are essential to memorize.
- 📈 The process of finding derivatives involves using limits and the concept of a derivative as a limit, which is a fundamental calculus technique.
- 🔄 The instructor demonstrates the derivation of the sine function using trigonometric identities and the limit process, showcasing the steps in a clear and methodical way.
- 📝 The script includes a detailed walkthrough of using the product rule to find the derivative of a function that is a product of two other functions, such as y = x * sin(x).
- 📉 The concept of the derivative as a slope function is discussed, with examples of how to find the slope at a particular point on a curve.
- 📌 The instructor provides an example of finding the equation of a tangent line to a curve at a specific point, using the point-slope form of a line.
- 🔢 The script touches on the cyclical nature of derivatives of trigonometric functions, such as sine and cosine, and how they relate to the oscillation of these functions.
- 🌐 A word problem involving a spring and mass system is introduced to illustrate how the concepts of derivatives can be applied to real-world physics scenarios.
- 🔑 The Chain Rule is introduced as an upcoming topic, which will be crucial for dealing with complex derivatives involving compositions of functions or large exponents.
- 🔍 The importance of precision and step-by-step work in calculus is emphasized, as opposed to trying to do calculations quickly in one's head, which can lead to errors.
Q & A
What is the main focus of the discussion in the transcript?
-The main focus of the discussion is on trigonometric functions and their derivatives, specifically how to find the derivatives of sine, cosine, tangent, secant, cosecant, and cotangent using various rules such as the product rule and the quotient rule.
Why are trigonometric functions important in calculus?
-Trigonometric functions are important in calculus because they are fundamental to many mathematical concepts and are often used in solving real-world problems. They also appear frequently in higher-level calculus courses and are essential for understanding more complex mathematical operations.
What is the derivative of sine with respect to x?
-The derivative of sine with respect to x is cosine, denoted as d(sin(x))/dx = cos(x).
How is the derivative of cosine related to sine?
-The derivative of cosine with respect to x is negative sine, denoted as d(cos(x))/dx = -sin(x).
What is the significance of the addition rule for sine in the proof of the derivative of sine?
-The addition rule for sine is used to split the sine of a sum (sin(x + h)) into two separate terms (sin(x)cos(h) + cos(x)sin(h)), which is crucial for simplifying the expression and finding the derivative of sine.
What is the product rule in calculus, and when is it used?
-The product rule in calculus is used when finding the derivative of a product of two functions. It states that the derivative of the product is the derivative of the first function times the second function plus the first function times the derivative of the second function. It is used in the transcript when finding the derivative of y = x*sin(x).
What is the quotient rule in calculus, and how is it applied?
-The quotient rule in calculus is used to find the derivative of a quotient of two functions. It states that the derivative of the quotient is the derivative of the numerator times the denominator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. It is hinted at in the transcript for functions like secant and cosecant.
How does the chain rule relate to the problems discussed in the transcript?
-The chain rule is mentioned as a method to deal with complex functions, especially those involving large exponents or compositions. It allows for the simplification of derivatives by treating the function as a composition, which can be particularly useful for functions like (1 + cos(x))^3.
What is the physical interpretation of the derivative of a function?
-The derivative of a function at a certain point represents the slope of the tangent line to the function at that point, which can be interpreted as the rate of change or velocity in physical contexts.
Can you provide an example of how to find the equation of a tangent line to a curve at a specific point using derivatives?
-Yes, to find the equation of a tangent line to a curve at a specific point, you first find the derivative of the function, which gives you the slope of the tangent line. Then, you plug the x-coordinate of the point into the derivative to find the slope (m). With the slope and the point (x, y), you can use the point-slope form of a line (y - y1 = m(x - x1)) to find the equation of the tangent line.
What is the cyclical nature of the derivatives of sine and cosine functions?
-The cyclical nature of the derivatives of sine and cosine functions refers to the pattern that emerges when you repeatedly take derivatives. For example, the derivative of sine is cosine, the derivative of cosine is negative sine, the derivative of negative sine is negative cosine, and so on, which leads back to sine after four derivatives.
Outlines
📚 Introduction to Trigonometric Functions and Derivatives
The speaker begins by introducing the topic of trigonometric functions, emphasizing the importance of understanding their derivatives as they are fundamental to various mathematical concepts. The talk is aimed at students who may feel overwhelmed but assures them of the necessity to grasp these basics for future studies. The focus is on the derivatives of sine, cosine, tangent, secant, cosecant, and cotangent, with an intention to demonstrate the derivation process using the limit concept and trigonometric identities.
🔍 Deriving the Derivative of Sine Using Limits and Trigonometric Identities
In this segment, the speaker delves into the process of deriving the derivative of the sine function. They explain the use of limits to find the derivative and introduce the concept of trigonometric identities necessary for the derivation. The explanation includes algebraic manipulation and the application of the sum of angles identity for sine. The goal is to express the derivative in terms of known functions and to understand the significance of the process in calculus.
📈 Memorizing Trigonometric Derivatives and Their Relationships
The speaker provides a comprehensive list of derivatives for common trigonometric functions, highlighting the need for memorization due to their frequent use in higher-level mathematics. They discuss the relationships between the derivatives of sine and cosine, as well as the derivatives of tangent, secant, cosecant, and cotangent. The segment also touches on the unique nature of the cosine derivative and its relation to the sine function.
📘 Applying Product Rule to Trigonometric Functions
This paragraph discusses the application of the product rule in deriving the slope of a function that is a product of two trigonometric functions. The speaker uses the example of y = x * sin(x) to illustrate the process, emphasizing the importance of recognizing when to apply the product rule and how to set it up correctly. The explanation includes the steps to find the derivative and the significance of the derivative as a slope function.
📝 Finding the Equation of a Tangent Line Using Derivatives
The speaker explains how to find the equation of a tangent line to a curve at a specific point using the concept of derivatives. They provide a step-by-step guide on using the point-slope form of a line, starting with finding the slope at a given point by plugging in the x-coordinate into the derivative function. The example of finding the tangent line at x = 2 for the function y = x * sin(x) is used to demonstrate the process.
🔢 Deriving Complex Trigonometric Functions Using Quotient Rule
The segment focuses on the derivation of more complex trigonometric functions, particularly those that involve a quotient, such as secant and cosecant. The speaker illustrates the use of the quotient rule and emphasizes the importance of setting up the derivative correctly, including the use of parentheses and the order of operations. The goal is to find the derivative of a function that involves a quotient of trigonometric expressions.
🔄 Understanding the Cyclical Nature of Trigonometric Derivatives
This part of the script explores the cyclical pattern observed when taking successive derivatives of trigonometric functions. The speaker explains how the derivatives of sine and cosine oscillate between positive and negative values, and how this relates to the periodic nature of these functions. They also discuss the implications of this pattern for the fourth derivative of sine and the behavior of the function's slope.
🌐 Modeling Oscillation with Trigonometric Functions
The speaker presents a word problem involving a spring oscillating back and forth, which can be modeled using a trigonometric function. They discuss the position function of the oscillating mass and its relation to the cosine function, taking into account the initial conditions. The focus is on understanding the behavior of the system and how it can be represented mathematically using trigonometric derivatives.
🔑 Introducing the Chain Rule for Complex Derivations
In the final paragraph, the speaker introduces the concept of the Chain Rule, which is essential for deriving complex functions, especially those involving large exponents or compositions. They explain the importance of the Chain Rule in simplifying the derivation process and set the stage for combining it with other rules like the product and quotient rules to tackle a wide range of derivative problems.
Mindmap
Keywords
💡Trigonometric functions
💡Derivative
💡Product rule
💡Quotient rule
💡Limit
💡Trigonometric identities
💡Chain rule
💡Slope
💡Tangent line
💡Word problem
Highlights
Introduction to the importance of trigonometric functions in calculus, emphasizing their frequent use even when not immediately apparent.
Explanation of the basics of trigonometric functions, setting the stage for more complex topics in the class.
The necessity of understanding the derivatives of sine, cosine, tangent, secant, cosecant, and cotangent for advanced mathematical applications.
Demonstration of the process to find the derivative of sine using limits and the concept of a derivative as a limit.
Use of trigonometric identities to simplify the expression for the derivative of sine, showcasing the interplay between algebra and trigonometry.
Clarification on the difference between the derivative of sine and cosine, and the importance of memorizing these basic derivatives.
Introduction of the product rule in calculus for finding derivatives of functions that are products of two other functions.
Application of the product rule to find the derivative of y = x * sin(x), illustrating a common technique in calculus.
Discussion on the significance of the derivative as a slope function, and how it can be used to find the equation of a tangent line.
Process of finding the equation of a tangent line at a specific point using the point-slope form of a line.
The cyclical nature of derivatives for trigonometric functions, such as sine and cosine, and their implications for understanding oscillation.
Introduction of a word problem involving a spring and mass system to demonstrate the application of derivatives in physics.
Derivation of the velocity function for the spring and mass system using the first derivative of the position function.
Explanation of how to find points of zero velocity in the spring and mass system, corresponding to changes in direction.
Introduction of the Chain Rule as a method for dealing with complex derivatives, especially those involving compositions of functions.
Highlighting the efficiency of the Chain Rule in simplifying the process of finding derivatives of composite functions.
Preview of the integration of different rules in calculus, such as the product, quotient, and Chain Rule, for solving a variety of derivative problems.
Transcripts
Browse More Related Video

Derivatives of Trig Functions (Sin, Cos, Tan) in Calculus - [1-4]

Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial
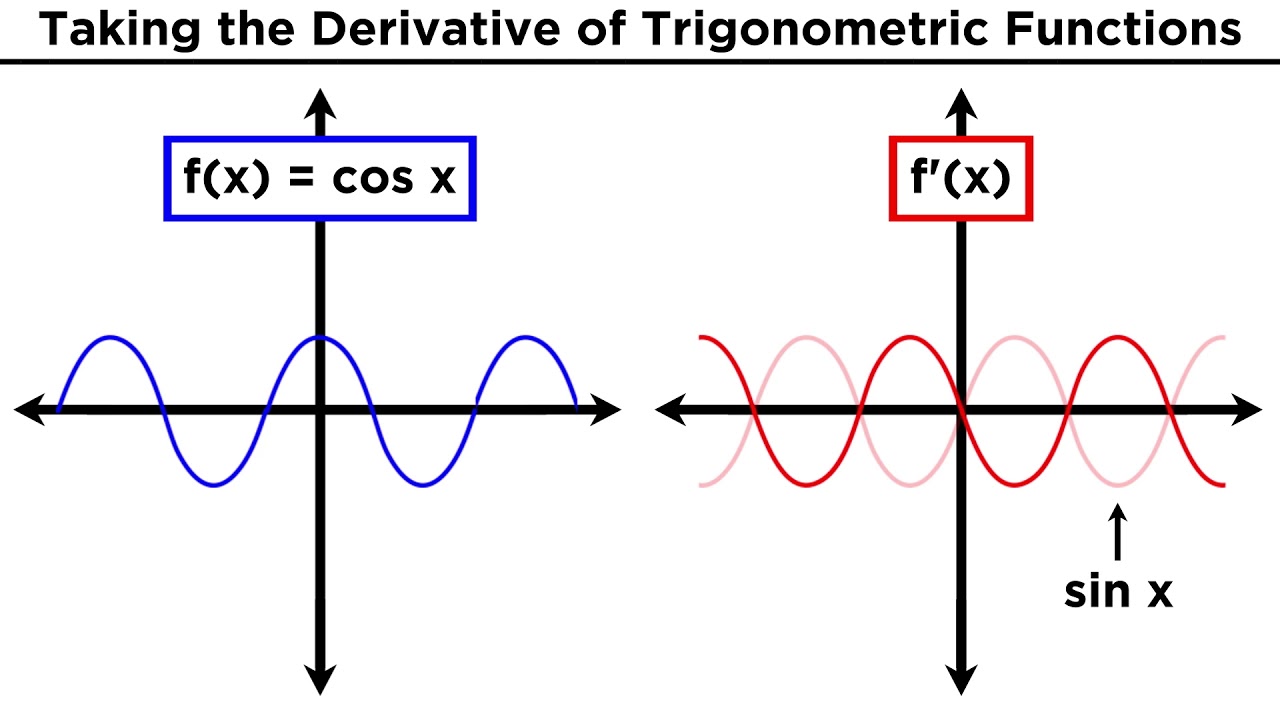
Derivatives of Trigonometric Functions
How To Find The Derivative of Sin^2(x), Sin(2x), Sin^2(2x), Tan3x, & Cos4x

Quotient Rule | MIT 18.01SC Single Variable Calculus, Fall 2010

Derivatives of Trigonometric Functions
5.0 / 5 (0 votes)
Thanks for rating: