Quotient Rule | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare
7 Jan 201104:21
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational segment, the professor guides students through the process of finding the derivative of tangent x using the quotient rule. The professor first reminds students of the quotient rule formula and then applies it to the trigonometric functions sine x and cosine x, which form the tangent function. After performing the differentiation, the professor simplifies the result using trigonometric identities, revealing that the derivative of tangent x is secant squared x. The lesson also touches on the potential for finding derivatives of other trigonometric functions like cotangent, cosecant, and secant using similar rules.

Takeaways
  • 📚 The session begins with a reminder of the quotient rule for differentiation, which is crucial for finding the derivative of functions expressed as a quotient of two other functions.
  • 🔍 The derivative of tangent x is the focus of the lesson, and it is approached by recognizing that tangent x is the quotient of sine x and cosine x.
  • 📝 The quotient rule formula is explicitly stated, setting the stage for the application to the specific functions sine x (u) and cosine x (v).
  • ✍️ The process of applying the quotient rule involves taking the derivative of the numerator and denominator, multiplying them appropriately, and then simplifying the result.
  • 📉 The derivative of sine x is cosine x, and the derivative of cosine x is negative sine x, which are the building blocks for the application of the quotient rule.
  • 🔢 The numerator simplifies to cosine squared x minus sine squared x, which can be further simplified using trigonometric identities.
  • 🧩 The trigonometric identity that the sum of sine squared x and cosine squared x equals 1 is used to simplify the expression to 1.
  • 💡 The simplification leads to the realization that the derivative of tangent x is secant squared x, which is 1 over cosine squared x.
  • 🔄 The method demonstrated can be applied to other trigonometric functions like cotangent, cosecant, and secant using the quotient rule.
  • 📈 The lesson emphasizes the importance of mastering the quotient rule and chain rule for finding derivatives of various trigonometric functions.
  • 🌟 The session concludes with the understanding that the derivative of tangent x is secant squared x, reinforcing the concept and its application.
Q & A

  • What is the objective of the recitation segment mentioned in the script?

    -The objective is to find the derivative of tangent x using the quotient rule.

  • What is the quotient rule in calculus?

    -The quotient rule is a method for finding the derivative of a function that is the ratio of two other functions. It states that the derivative of u/v is (v*u' - u*v')/v², where u and v are functions of x.

  • Why can the quotient rule be used to find the derivative of tangent x?

    -The quotient rule can be used because tangent x is expressed as the quotient of two functions: sine x (u) and cosine x (v).

  • What are the steps to find the derivative of tangent x using the quotient rule?

    -1. Identify u and v: u = sine x, v = cosine x. 2. Compute u' (derivative of sine x) and v' (derivative of cosine x). 3. Apply the quotient rule formula: (v*u' - u*v')/v².

  • What is the derivative of sine x?

    -The derivative of sine x is cosine x.

  • What is the derivative of cosine x?

    -The derivative of cosine x is negative sine x.

  • What simplification can be made using trigonometric identities when finding the derivative of tangent x?

    -The numerator, cosine²x + sine²x, simplifies to 1 using the identity cosine²x + sine²x = 1. The expression then simplifies to 1/cosine²x, which equals secant²x.

  • What is the derivative of tangent x?

    -The derivative of tangent x is secant squared x (sec²x).

  • What other trigonometric functions can be differentiated using the quotient rule as mentioned in the script?

    -Other functions include cotangent x, cosecant x, and secant x.

  • How can the derivative of secant x be found using the quotient rule?

    -To find the derivative of secant x, one can take the derivative of 1/cosine x using the quotient rule.

Outlines
00:00
📚 Derivative of Tangent x Using Quotient Rule

This paragraph introduces a recitation segment focused on finding the derivative of the tangent function using the quotient rule. The professor reminds students of the quotient rule formula and its application to the derivative of tangent x, which is expressed as the quotient of sine x and cosine x. The students are given a hint to work out the problem themselves before the professor demonstrates the process. The explanation involves taking the derivative of sine x and multiplying it by the denominator, then subtracting the product of the derivative of cosine x and the original numerator, all divided by the square of the denominator. The paragraph concludes with the simplification using trigonometric identities, resulting in the derivative of tangent x being secant squared x.

Mindmap
Keywords
💡recitation
Recitation refers to a session in which students practice and review material, often under the guidance of an instructor. In the context of the video, it is the setting where the professor is guiding students through a mathematical concept. The script mentions 'Welcome back to recitation' indicating the educational nature of the session.
💡derivative
A derivative in calculus is a measure of how a function changes as its input changes. It is a fundamental concept in the study of rates of change. The video's main theme revolves around finding the derivative of the tangent function using a specific rule, emphasizing the importance of derivatives in understanding the behavior of functions.
💡quotient rule
The quotient rule is a mathematical rule used to find the derivative of a function that is the quotient of two other functions. The script explicitly asks students to use this rule to find the derivative of tangent x, highlighting its application in deriving new functions from existing ones.
💡tangent
In trigonometry, the tangent of an angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side. In the context of calculus, the tangent function is one of the basic trigonometric functions for which the derivative is being sought in the video.
💡sine
The sine function is one of the fundamental trigonometric functions that relates the ratio of the lengths of sides of a right triangle to the angle measured in radians. In the script, sine x is identified as the numerator in the expression for the tangent function, which is then used in applying the quotient rule.
💡cosine
The cosine function, like sine, is a trigonometric function that represents the ratio of the adjacent side to the hypotenuse in a right triangle. In the video, cosine x is the denominator in the tangent function's expression and plays a crucial role in the quotient rule application.
💡trigonometric identities
Trigonometric identities are equations that hold true for all values of the variables and are used to simplify trigonometric expressions. The script mentions using trigonometric identities to simplify the expression obtained after applying the quotient rule, showing their utility in simplifying complex expressions.
💡secant
Secant is the reciprocal of the cosine function, denoted as sec(x) = 1/cos(x). In the video, the professor simplifies the derivative of tangent to involve secant squared, demonstrating how the secant function emerges from the derivative of tangent.
💡chain rule
The chain rule is another fundamental rule in calculus for finding the derivative of a composite function. While the script primarily focuses on the quotient rule, it briefly mentions the chain rule as an alternative method for finding the derivative of secant x, indicating the versatility of calculus rules.
💡cotangent
Cotangent, often abbreviated as cot, is the reciprocal of the tangent function, and it is another basic trigonometric function. The script suggests that the quotient rule can also be used to find the derivative of cotangent, along with other trigonometric functions, showcasing the rule's broad applicability.
💡cosecante
Cosecant, or cosec, is the reciprocal of the sine function, denoted as csc(x) = 1/sin(x). The script implies that the derivative of cosecant can also be found using the quotient rule, further emphasizing the rule's utility in trigonometric calculus.
Highlights

Introduction to the recitation segment focusing on the derivative of tangent x.

Reminder of the quotient rule for derivatives, where u and v are functions of x.

The derivative of tangent x is to be found using the quotient rule.

Tangent x is recognized as a quotient of sine x and cosine x.

Demonstration of the quotient rule application to find the derivative of tangent x.

Derivative of sine x is identified as cosine x.

Multiplication of the derivative of sine x with the denominator, cosine x.

Subtraction of the derivative of cosine x, which is negative sine x, from the first term.

Simplification of the expression using trigonometric identities.

Mention of the identity cosine squared x plus sine squared x equals 1.

Simplification of the numerator to 1 and the denominator to cosine squared x.

Identification of the resulting function as secant squared x.

Discussion on alternative methods to simplify the derivative of tangent x.

Application of the quotient rule to other trigonometric functions like cotangent, cosecant, and secant.

Suggestion to use the quotient rule or chain rule to find the derivative of secant x.

Emphasis on building a repertoire of derivatives using different rules.

Transcripts

Browse More Related Video

Derivative of Inverse Trig Functions via Implicit Differentiation

Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial

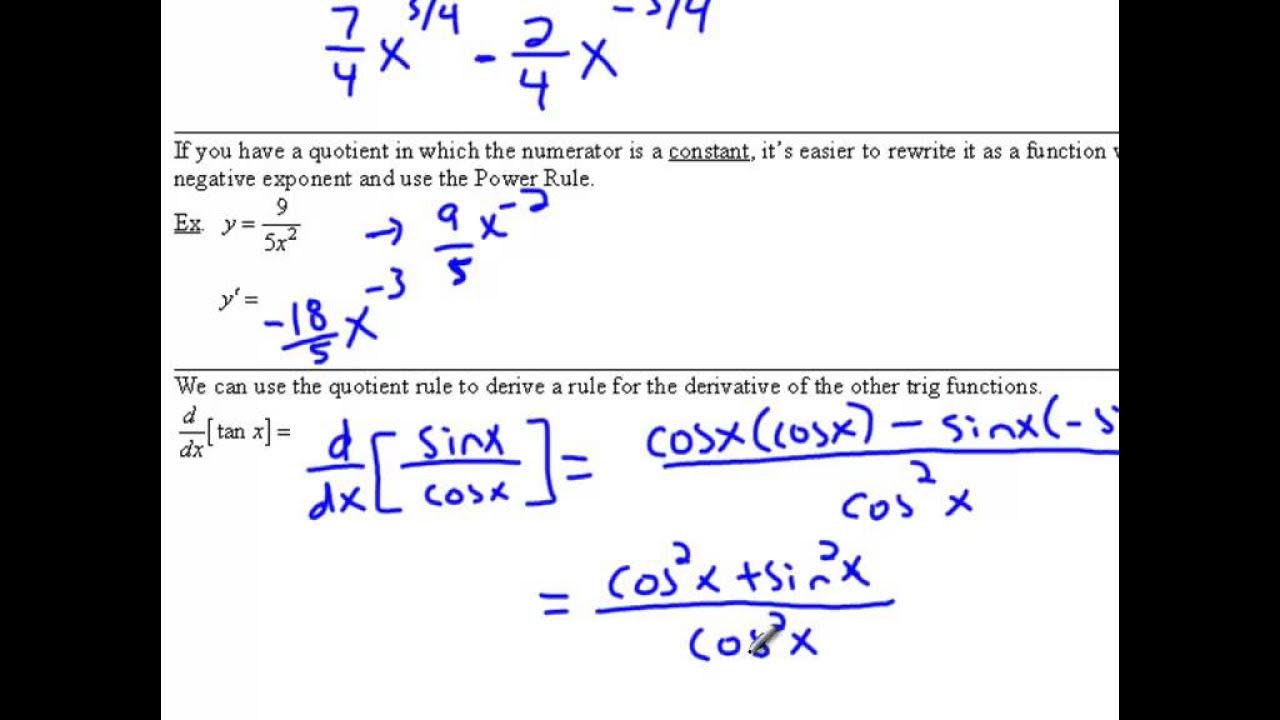
Product and Quotient Rule

Derivatives of Trigonometric Functions

The derivative of Trigonometric Functions

Log and Exponent Derivatives | MIT 18.01SC Single Variable Calculus, Fall 2010

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DerivativeTangent xQuotient RuleTrigonometryEducationalMath TutorialSine xCosine xTrig IdentitiesSecant xChain Rule