Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial

The Organic Chemistry Tutor

10 Sept 201635:01

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers an in-depth exploration of the derivatives of trigonometric functions, essential for calculus students. It begins by listing the derivatives of basic trigonometric functions, such as sine, cosine, and tangent, and then extends to more complex ones like cosecant, cotangent, and secant. The script uses the power rule and the product, quotient, and chain rules to derive the first derivatives of various trigonometric expressions, including composite functions. It also demonstrates how to apply these rules to solve problems involving functions like x cubed plus sine x plus 4 cosine x. The video concludes with proofs for the derivatives of secant and cotangent functions, reinforcing the understanding of the underlying mathematical principles. The comprehensive approach and step-by-step explanations make this script a valuable resource for grasping the intricacies of trigonometric derivatives.

Takeaways

📚 The derivative of sin(x) is cos(x), which is a fundamental rule for differentiation of trigonometric functions.
📉 The derivative of cos(x) is -sin(x), indicating a negative relationship between the derivative of cosine and sine.
📈 The derivative of tan(x) is sec^2(x), which involves the secant function squared.
🔄 A pattern exists for derivatives with a 'c' in the function name (cosec, cotan), as they tend to have a negative sign in front.
👆 The power rule for derivatives states that the derivative of x^n is n*x^(n-1), which is crucial for polynomial functions.
🤝 The product rule for derivatives is applied when two functions are multiplied, expressed as (f'g + fg') for functions f and g.
➗ The quotient rule for derivatives is used for rational functions, given by (g*f' - f*g') / g^2, where f and g are the numerator and denominator functions, respectively.
⛓ The chain rule is essential for composite functions, expressed as f'(g(x)) * g'(x), where f is the outer function and g is the inner function.
🔢 For composite functions involving trigonometric functions, apply the chain rule by differentiating the outer function and then multiplying by the derivative of the inner function.
📌 Memorizing the derivatives of the six basic trigonometric functions is key to solving more complex trigonometric differentiation problems.
📐 The proof of derivatives for secant and cotangent functions involves applying the power rule and quotient rule, showcasing the relationship between trigonometric identities and derivatives.

Q & A

What is the derivative of sine(x)?
-The derivative of sine(x) is cosine(x).
How do you find the derivative of a function that is a product of two functions?
-You use the product rule, which states that the derivative of a function f(x) times g(x) is f'(x) times g(x) plus f(x) times g'(x).
What is the derivative of tangent(x) with respect to x?
-The derivative of tangent(x) with respect to x is secant squared(x).
What is the general rule for memorizing the derivatives of the trigonometric functions that include 'cosecant', 'cosine', or 'cotangent'?
-There is usually a negative sign in front of the derivative when the original function includes 'cosecant', 'cosine', or 'cotangent'.
What is the derivative of x cubed with respect to x?
-The derivative of x cubed with respect to x is 3x squared, according to the power rule.
How do you apply the quotient rule to find the derivative of a function in the form of f(x)/g(x)?
-The quotient rule states that the derivative of f(x)/g(x) is [g(x) * f'(x) - f(x) * g'(x)] / [g(x)]^2.
What is the derivative of the composite function f(g(x))?
-The derivative of the composite function f(g(x)) is f'(g(x)) * g'(x), where f' denotes the derivative of f and g' denotes the derivative of g.
How do you prove that the derivative of secant(x) is secant(x) tangent(x)?
-You use the power rule and chain rule, rewriting secant(x) as 1/cosine(x), then differentiating and simplifying to show it equals secant(x) tangent(x).
What is the derivative of y with respect to x if y equals x squared sine(x)?
-Using the product rule, the derivative is 2x sine(x) plus x squared cosine(x).
How do you find the derivative of a function that includes a trigonometric function inside another, such as tangent(sine(4x))?
-You use the chain rule, differentiating the outer function first while keeping the inner function the same, and then multiply by the derivative of the inner function.
What is the derivative of y with respect to x if y equals sine squared(3x)?
-First, rewrite sine squared(3x) as [sine(3x)]^2, then apply the power rule to get 2 sine(3x) times the derivative of sine(3x), which is 2 sine(3x) times cosine(3x).

Outlines

00:00

📚 Introduction to Trigonometric Derivatives

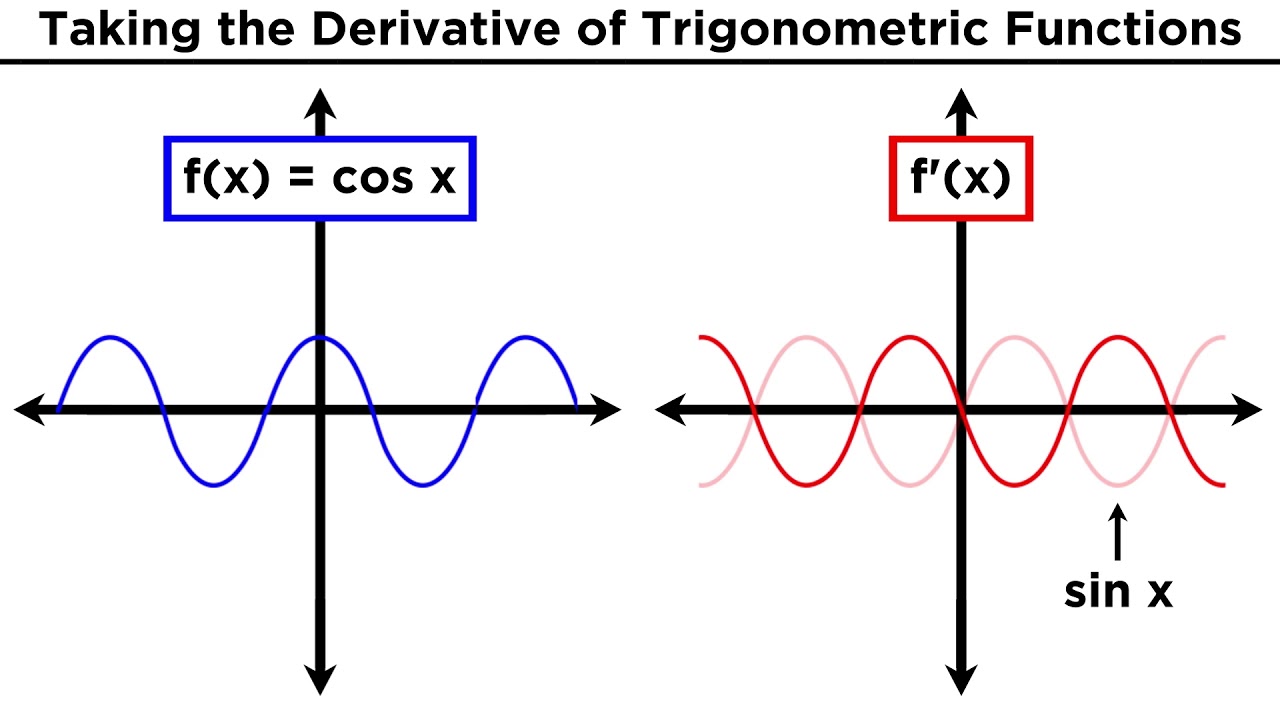
This paragraph introduces the derivatives of basic trigonometric functions. It explains that the derivative of sine(x) is cosine(x), the derivative of cosine(x) is negative sine(x), and the derivative of tangent(x) is secant squared(x). It also covers the derivatives of cosecant(x), cotangent(x), and cotan(x), noting a negative sign is usually associated with functions that include 'co-'. The paragraph then applies this knowledge to find the derivative of a function f(x) = x^3 + sin(x) + 4cos(x), resulting in f'(x) = 3x^2 + cos(x) - 4sin(x).

05:01

🔍 Applying Product and Quotient Rules

The second paragraph delves into applying the product and quotient rules for derivatives. It discusses how to find the derivative of a function that is a product of two functions using the formula f'(x)g(x) + g'(x)f(x), and for a quotient, the formula g(x)f'(x) - f(x)g'(x) / g(x)^2. Examples include finding the derivatives of functions like y = x^2sin(x), y = x^3cos(x), and y = sin(x)/x^2, with the latter using the quotient rule. The paragraph emphasizes the importance of factoring out common terms and canceling where possible to simplify the expressions.

10:02

🔗 Chain Rule for Composite Functions

The third paragraph focuses on the chain rule for composite functions. It explains that the derivative of a composite function f(g(x)) is found by multiplying the derivative of the outer function f' by the derivative of the inner function g'. The paragraph provides formulas for the derivatives of functions like sine(u), cosine(u), and tangent(u), where u is an inner function. It then applies these formulas to find the derivatives of functions such as f(x) = sin(5x) and f(x) = cos(x^3), demonstrating the process of differentiating from the outside in.

15:03

🔧 Power Rule and Trigonometric Derivatives

The fourth paragraph discusses the application of the power rule in conjunction with the derivatives of trigonometric functions. It covers how to handle functions raised to a power, such as secant(x)^2, and how to find the derivative of nested trigonometric functions like tangent(sin(4x)). The paragraph also explains how to rewrite functions to make differentiation simpler, such as squaring sine(3x) and differentiating it using the power rule and chain rule.

20:04

📝 Derivatives of Complex Trigonometric Expressions

The fifth paragraph continues with the theme of complex trigonometric expressions, showing how to differentiate expressions like cotangent to the fourth power of sine(x) cubed. It demonstrates the use of the power rule to move exponents outside of functions and the chain rule to differentiate nested functions. The paragraph also covers the differentiation of functions like y = secant(x) squared and y = tangent(sin(4x)), emphasizing the step-by-step process of applying the chain rule.

25:06

📐 Proving Derivatives of Trigonometric Functions

The sixth paragraph shifts the focus to proving the derivatives of trigonometric functions, such as secant(x) and cotangent(x). It uses the quotient rule and trigonometric identities to show that the derivative of secant(x) is indeed secant(x)tangent(x) and that the derivative of cotangent(x) is negative cosecant(x) squared. The paragraph emphasizes the importance of understanding the underlying principles of differentiation and the application of trigonometric identities in proving these derivatives.

30:06

📝 Final Thoughts and Thanks

The seventh and final paragraph wraps up the video with a brief summary of the concepts covered and a thank you to the viewers. It does not contain substantial mathematical content but serves as a conclusion to the video, encouraging viewers to apply what they've learned and to continue exploring the topic of derivatives.

Mindmap

Keywords

💡Derivative

A derivative in calculus represents the rate at which a function changes with respect to a variable. In the context of the video, it is the central theme as it discusses the derivatives of various trigonometric functions, such as sine and cosine, which are fundamental to understanding the rate of change in these functions.

💡Trigonometric functions

Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides. In the video, these functions, including sine, cosine, and tangent, are used to demonstrate how their derivatives are calculated and applied in mathematical problems.

💡Power rule

The power rule is a basic rule in calculus that allows the differentiation of polynomial terms. It states that the derivative of x to the power of n (x^n) is n times x to the power of (n-1). In the video, the power rule is used to find the derivatives of terms like x cubed, which is 3x squared.

💡Product rule

The product rule is a formula used in calculus to find the derivative of a product of two functions. It is given as (f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x). The video demonstrates the use of the product rule in finding the derivatives of functions like x squared sine x.

💡Quotient rule

The quotient rule is a method used to find the derivative of a quotient of two functions. It is expressed as (f(x) / g(x))' = (g(x) * f'(x) - f(x) * g'(x)) / (g(x))^2. The video uses the quotient rule to differentiate functions in the form of one function divided by another, such as sine x over x squared.

💡Chain rule

The chain rule is a technique used to differentiate composite functions. It states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. The video illustrates the chain rule's application when differentiating functions like sine of 5x.

💡Secant function

The secant function, sec(x), is the reciprocal of the cosine function, or 1/cos(x). In the video, the derivative of the secant function is discussed, showing that the derivative of sec(x) is sec(x)tan(x), which is a direct result of applying the power rule and chain rule.

💡Cosecant function

Cosecant, csc(x), is another reciprocal trigonometric function defined as 1/sin(x). The video explains that the derivative of cosecant x is negative cosecant x times cotangent x, which is derived using the chain rule and the properties of the cosecant function.

💡Cotangent function

Cotangent, cot(x), is the reciprocal of the tangent function, or cos(x)/sin(x). The video covers the derivative of cotangent x, which is shown to be negative cosecant squared x. This is proven using the quotient rule and trigonometric identities.

💡Tangent function

The tangent function, tan(x), is the ratio of the sine to the cosine function, or sin(x)/cos(x). The video discusses the derivative of the tangent function, which is secant squared x, and uses this information to solve problems involving tangent in the derivative calculations.

💡Trigonometric identities

Trigonometric identities are equations that hold true for all values of the variables under consideration. They are used to simplify and manipulate trigonometric expressions. In the video, identities like sin^2(x) + cos^2(x) = 1 are used to prove the derivatives of functions like cotangent x and secant x.

Highlights

Derivative of sine(x) is equal to cosine(x)

Derivative of cosine(x) is equal to negative sine(x)

Derivative of tangent(x) is equal to secant squared(x)

Derivative of cosecant(x) is equal to negative cosecant(x) cotangent(x)

Derivative of secant(x) is secant(x) tangent(x)

Derivative of cotangent(x) is negative cosecant squared(x)

A pattern for derivatives with a 'c' in the function name often includes a negative sign

The derivative of x cubed plus sine(x) plus 4 cosine(x) is 3x squared plus cosine(x) minus 4 sine(x)

Derivatives of functions involving trigonometric functions can be found using the power rule and basic trigonometric derivative properties

Product rule for derivatives is f'(x)g(x) + f(x)g'(x), where f and g are functions of x

Quotient rule for derivatives is [g(x)f'(x) - f(x)g'(x)] / [g(x)]^2 for functions f and g

Chain rule for derivatives involves differentiating the outside function and multiplying by the derivative of the inside function

Derivative of sine(u) is cosine(u) times the derivative of u

Derivative of cosine(x cubed) is negative 3x squared sine(x cubed) using the chain rule

Derivative of secant(x squared) is 2x secant(x squared) tangent(x squared)

Derivative of tangent(sine(4x)) involves applying the chain rule step by step from the outside function inwards

Derivative of sine squared(3x) is 6 sine(3x) cosine(3x) after applying the power rule and chain rule

Derivative of cotangent to the fourth of sine(x cubed) is a complex application of the power rule and chain rule

Proving the derivative of secant(x) is secant(x) tangent(x) involves using the power rule and trigonometric identities

Proving the derivative of cotangent(x) is negative cosecant squared(x) uses the quotient rule and trigonometric identities

Transcripts

Browse More Related Video

Derivatives of Trig Functions (Sin, Cos, Tan) in Calculus - [1-4]

Derivatives of Trigonometric Functions

Quotient Rule | MIT 18.01SC Single Variable Calculus, Fall 2010

Derivatives of Trig Functions - Calculus | MCV4U

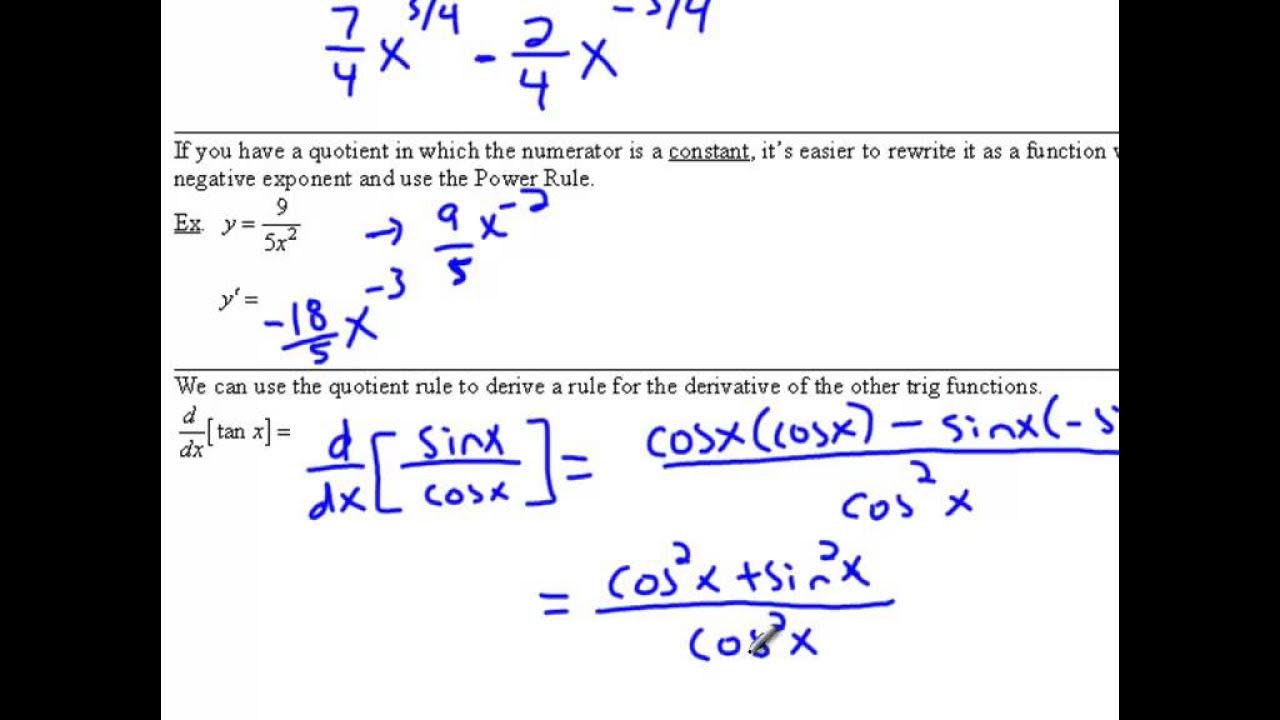
Product and Quotient Rule

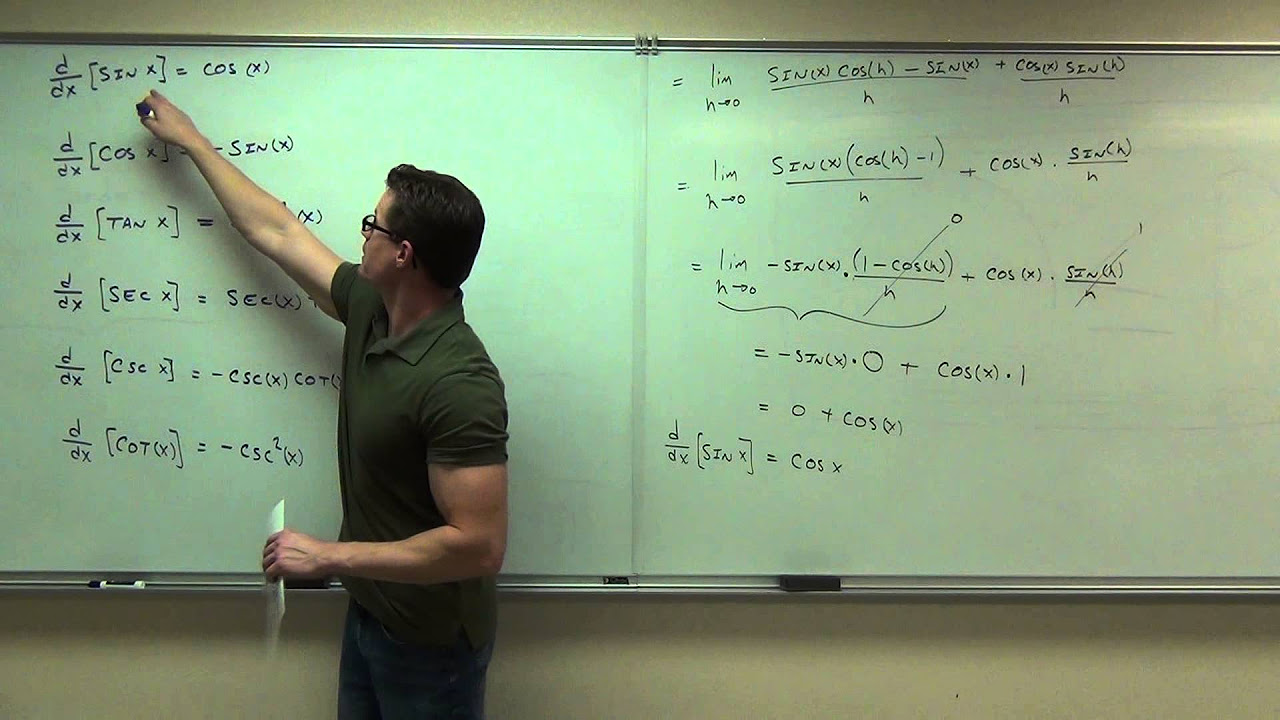
Calculus 1 Lecture 2.5: Finding Derivatives of Trigonometric Functions

Related Tags

Trigonometric Derivatives Calculus Tutorial Sine Function Cosine Function Tangent Derivative Chain Rule Product Rule Quotient Rule Trig Identities Math Education Derivative Examples