Derivatives of Trig Functions (Sin, Cos, Tan) in Calculus - [1-4]
TLDRThis transcript from a calculus class focuses on the derivatives of trigonometric functions, such as sine, cosine, tangent, cotangent, secant, and cosecant. The instructor emphasizes the importance of understanding and memorizing these derivatives for problem-solving. Through examples, the class demonstrates how to apply rules like the chain rule and the multiplication and division rules to find derivatives of more complex trigonometric expressions. The goal is to help students grasp the concept of derivatives as slopes of functions and to become proficient in using the formulas for derivatives in trigonometry.
Takeaways
- 📚 The derivatives of trigonometric functions are crucial for solving calculus problems involving sine, cosine, tangent, and their reciprocals.
- 🔄 Derivative of sine is cosine, and the derivative of cosine is negative sine, showing an inverse relationship.
- 🌐 The derivative of tangent is secant squared, and the derivative of cotangent is negative cosecant squared, highlighting the connections between trigonometric functions.
- 📈 The concept of derivatives relates to the slope of a function, which can be visualized by comparing the trigonometric functions' graphs.
- 🤝 Symmetry exists in the derivatives of trig functions, such as negative signs and squared terms, which can be helpful in memorization and application.
- 📝 The process of taking derivatives involves using specific formulas and rules, like the multiplication and division rules, for functions involving trigonometric expressions.
- 🧠 Memorizing the derivatives of trig functions is essential, and using mnemonic devices like the 'rainbow' can aid in recall.
- 🔢 Simplification of derived expressions is not always necessary, but understanding the process of deriving them is key to solving more complex problems.
- 📊 The appearance of the final derivative form can be complex, but it represents the slope of the original function, which can be analyzed using graphical methods.
- 🎯 Familiarity with trigonometric identities, such as the Pythagorean identity (cosine squared + sine squared = 1), is vital for simplifying derivatives.
- 🛠️ Practice is crucial for mastering the application of derivative rules to trigonometric functions, leading to more efficient problem-solving.
Q & A
What are the main topics covered in the transcript?
-The transcript covers the derivatives of trigonometric functions, including sine, cosine, tangent, cotangent, secant, and cosecant. It also discusses the process of finding derivatives and how they relate to the slope of a function's graph.
What is the derivative of sine with respect to X?
-The derivative of sine with respect to X is equal to cosine of X.
How is the derivative of cosine related to the derivative of sine?
-The derivative of cosine is the negative sine, making them opposites of each other with a negative sign involved.
What rule is used when taking the derivative of a function divided by another function?
-The quotient rule is used, which states that the derivative of a function divided by another is the bottom times the derivative of the top minus the top times the derivative of the bottom, divided by the bottom squared.
What is the process for finding the derivative of the tangent function?
-The derivative of the tangent function is found by using the definition of tangent as sine divided by cosine and applying the quotient rule to find that the derivative is equal to secant squared.
What is a key identity that can be used to simplify the expression secant squared minus tangent squared?
-A key identity used to simplify the expression is that tangent squared plus 1 is equal to secant squared, which implies that secant squared minus tangent squared equals 1.
How does the concept of a derivative relate to the slope of a function's graph?
-The derivative of a function represents the slope of the function at any given point on its graph, indicating how steep the function is at various points along its path.
What is the derivative of the function (x^2 * tan(x)) / secant(x)?
-The derivative of the function (x^2 * tan(x)) / secant(x) is x^2(secant^2(x) - tan^2(x)) + 2x * tan(x) / secant(x). This simplifies to x^2 + 2x * tan(x) / secant(x), using the trigonometric identity mentioned earlier.
How does the instructor suggest remembering the derivatives of trigonometric functions?
-The instructor suggests writing down the trigonometric functions in a specific order (sine, cosine, tangent, cotangent, secant, cosecant) and creating a 'rainbow' to associate each function with its reciprocal counterpart (e.g., 1/cosine is equal to secant), which can help in memorizing the derivatives.
What is the significance of the chain rule when taking derivatives of trigonometric functions multiplied together?
-The chain rule is significant in these cases as it allows the calculation of the derivative by treating each trigonometric function as individual components and applying the multiplication rule to find the derivative of the entire expression.
Outlines
📚 Introduction to Trigonometric Derivatives
This paragraph introduces the concept of derivatives of trigonometric functions, specifically focusing on sine, cosine, tangent, secant, cotangent, and cosecant. The instructor emphasizes that the goal is not to derive these functions in detail, but to understand which identities and derivatives are essential for problem-solving. The paragraph outlines the basic derivatives: the derivative of sine is cosine, cosine's derivative is negative sine, tangent's derivative is secant squared, cotangent's derivative is negative cosecant squared, secant's derivative is the product of tangent and secant, and cosecant's derivative is negative cotangent times cosecant. The instructor also highlights the symmetry in these derivatives and their relationship to the slopes of the corresponding trigonometric functions.
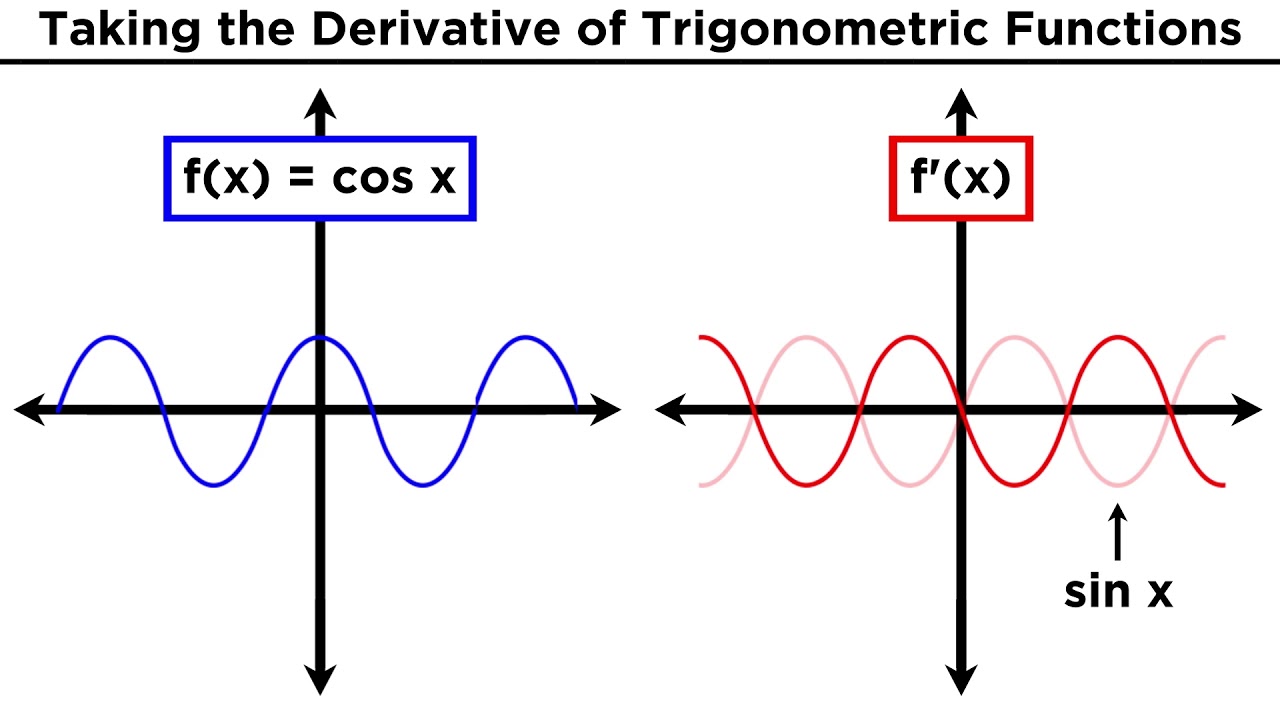
📈 Visualizing Derivatives and Slopes
The instructor uses visual aids to explain the relationship between the derivative of a function and its slope. By examining the sine and cosine functions, the instructor demonstrates how the derivative, or the slope of the sine function, is represented by the cosine function. This visual approach helps to clarify how the steepness of the sine function at any point corresponds to the value of the cosine function at that point. The paragraph also discusses the concept of cyclic trigonometric functions and their derivatives, reinforcing the idea of symmetry and the interplay between different trigonometric functions.
🧠 Deriving Tangent using Trigonometric Identities
This section delves into the process of deriving the derivative of the tangent function, which is shown to be equal to secant squared. The instructor uses the definition of tangent as the ratio of sine to cosine and applies the formula for the derivative of a quotient. Through the use of trigonometric identities and algebraic manipulation, the instructor simplifies the expression to arrive at the result. This paragraph serves as an example to illustrate the method of deriving trigonometric functions and their relationships, encouraging students to recognize and apply these techniques in their own problem-solving.
📝 Applying Derivatives to Trigonometric Functions
The instructor provides a step-by-step guide on how to apply derivatives to various trigonometric functions. The paragraph covers the derivative of the sum of sine and cosine, the product of cosecant and cotangent, and the ratio of tangent to x. The process involves using the basic rules of differentiation, such as the sum rule, product rule, and quotient rule, in the context of trigonometric functions. The instructor emphasizes the importance of memorizing the derivatives and applying the formulas correctly to solve problems.
🔢 Complex Derivatives and Trigonometric Identities
This paragraph tackles more complex derivatives involving multiple terms and trigonometric identities. The instructor demonstrates how to handle the derivative of a product of functions, such as x to the minus 3 power times sine of x times tangent of x. By applying the product rule and using trigonometric identities, the instructor simplifies the expression to a more manageable form. The paragraph reinforces the idea that while the answers may appear complicated, they are fundamentally representations of the slope of the function, which is the primary concept of derivatives.
📊 Division Rule and Trigonometric Derivatives
The paragraph focuses on using the division rule to find the derivatives of trigonometric functions. The instructor works through a problem involving the division of x squared times tangent of x by secant of x. By applying the quotient rule and distributing the terms, the instructor simplifies the expression and cancels out common factors. The process highlights the importance of recognizing and applying trigonometric identities to streamline the solution and arrive at the final answer.
🎓 Summary of Trigonometric Derivatives
In this final paragraph, the instructor summarizes the process of deriving trigonometric functions and emphasizes the big picture concept of derivatives as representations of the slope of a function. The paragraph reinforces the importance of understanding and applying the basic rules of differentiation, especially in the context of trigonometric functions. The instructor also encourages students to remember key trigonometric identities and to visualize the functions and their derivatives to gain a deeper understanding of the material.
Mindmap
Keywords
💡Derivatives
💡Trigonometric Functions
💡Sine Function
💡Cosine Function
💡Tangent Function
💡Secant Function
💡Chain Rule
💡Quadratic Functions
💡Power Rule
💡Trigonometric Identities
💡Symmetry
Highlights
Introduction to trigonometric function derivatives
Derivative of sine with respect to X is equal to cosine of x
Derivative of cosine with respect to X is negative sine
Derivative of tangent with respect to X is secant squared
Derivative of cotangent with respect to X is negative cosecant squared
Derivative of secant with respect to X is tangent times secant
Derivative of cosecant with respect to X is negative cotangent
Explanation of the symmetry in trigonometric function derivatives
Visualization of the sine and cosine functions and their derivatives
Derivative of a function divided by another function using the quotient rule
Derivation of the derivative of tangent as secant squared
Use of trigonometric identities in simplifying derivatives
Chain rule application in taking derivatives of complex expressions
Memorising trigonometric function derivatives for problem-solving
Working through a problem involving the derivative of sine and cosine
Derivative of a product of two trigonometric functions using the product rule
Handling division in derivatives with complex trigonometric expressions
Simplification of derivatives using fundamental trigonometric identities
The big picture of derivatives as representations of a function's slope
Transcripts
Browse More Related Video

Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial
Derivatives of Trigonometric Functions
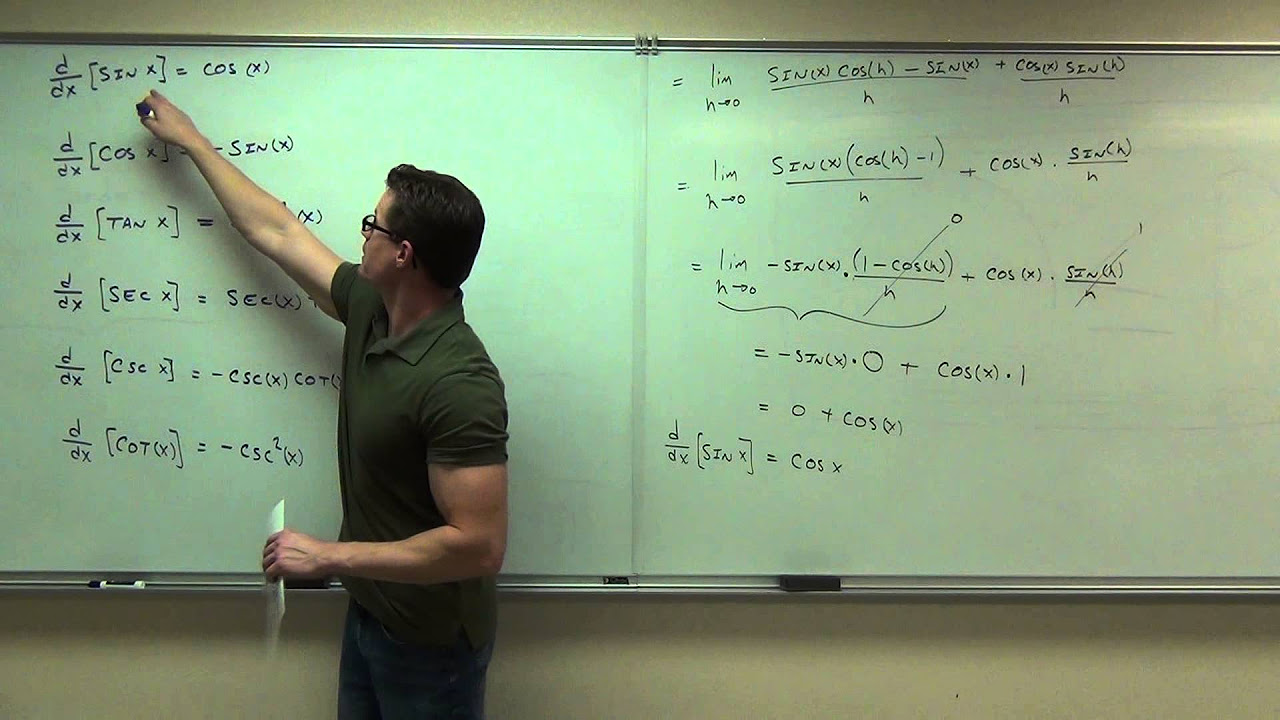
Calculus 1 Lecture 2.5: Finding Derivatives of Trigonometric Functions

AP Calculus AB: Lesson 3.1 Elementary Derivative Rules

Quotient Rule | MIT 18.01SC Single Variable Calculus, Fall 2010

Derivatives of Trigonometric Functions
5.0 / 5 (0 votes)
Thanks for rating: