Derivatives of Trigonometric Functions

The Organic Chemistry Tutor
24 Feb 201805:26
EducationalLearning
32 Likes 10 Comments

TLDRThis transcript delves into the derivatives of trigonometric functions, highlighting the six fundamental ones. It explains the derivatives of sine and cosine, and then introduces a pattern for the derivatives of tangent, cotangent, secant, and cosecant. The video provides examples of applying these derivatives to expressions, demonstrating the process of differentiation. The emphasis on recognizing cofunctions and their derivatives, particularly those starting with 'c' which have a negative sign, is a key takeaway. The examples solidify the understanding of trigonometric derivatives and their relationships.

Takeaways
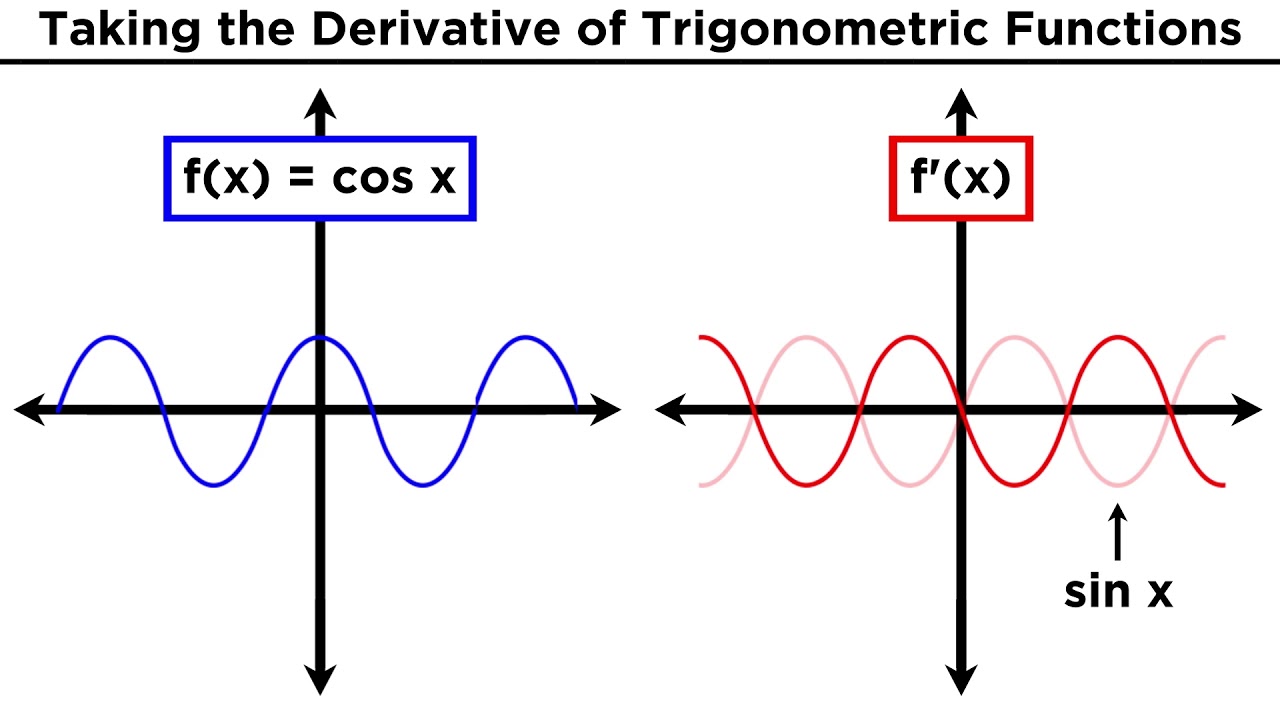
  • 📚 The derivative of sine x is cosine x.
  • 📈 The derivative of cosine x is negative sine x.
  • 🔄 For tan and cot, their derivatives are related to secant and cosecant squared respectively.
  • 📊 The derivative of tangent (tan x) is secant squared (sec^2 x).
  • 📉 The derivative of cotangent (cot x) is negative cosecant squared (-csc^2 x).
  • 🔢 The derivative of secant (sec x) is sec x multiplied by tangent (tan x).
  • 📐 The derivative of cosecant (csc x) is negative cosecant x times cotangent (-csc x * cot x).
  • 🧩 Cofunctions starting with 'c' (like cotangent and cosecant) have negative derivatives.
  • 🤝 Similarities exist between the derivatives of tan and cot, as well as secant and cosecant.
  • 📝 To find the derivative of a trigonometric expression, distribute the derivative of each term.
  • 🌟 Knowing the derivatives of sine, tangent, and secant allows one to determine the derivatives of the other functions.
Q & A

  • What is the derivative of sine x?

    -The derivative of sine x is cosine x.

  • What is the derivative of cosine x?

    -The derivative of cosine x is negative sine x.

  • What pattern can be observed in the derivatives of trigonometric functions that start with a 'c'?

    -The derivatives of trigonometric functions that start with a 'c', particularly cofunctions like cotangent, have a negative sign.

  • How are the derivatives of tan and cotan related?

    -The derivative of tangent is secant squared, and the derivative of cotangent is negative cosecant squared. They are related through their respective cofunctions and the signs of their derivatives.

  • What is the derivative of tangent x when multiplied by a constant?

    -When a constant is multiplied by tangent x, the derivative is the constant times the derivative of tangent x. So, the derivative of 'n' times tangent x is 'n' times secant squared.

  • What is the derivative of the expression 5 sine x - 4 tangent x?

    -The derivative of the expression 5 sine x - 4 tangent x is 5 cosine x - 4 secant squared x.

  • How do you find the derivative of 8 secant x - 5 cosine x?

    -The derivative of 8 secant x - 5 cosine x is 8 secant x tangent x + 5 sine x, based on the derivatives of secant and cosine x.

  • What is the derivative of cotangent x?

    -The derivative of cotangent x is negative cosecant squared x, due to the pattern observed with cofunctions starting with 'c'.

  • What is the derivative of the expression 2 cotangent x - 7 cosecant x?

    -The derivative of the expression 2 cotangent x - 7 cosecant x is negative 2 cosecant squared x + 7 cosecant x cotangent x.

  • How can you simplify the derivative of the expression 2 cotangent x - 7 cosecant x?

    -You can factor out the greatest common factor, which is cosecant x, to simplify the derivative to -2 cosecant squared x + 7 cosecant x cotangent x.

  • Why is it important to know the derivatives of sine, tangent, and secant?

    -Knowing the derivatives of sine, tangent, and secant is crucial because they form the basis for understanding the derivatives of other trigonometric functions, as seen in the patterns and relationships between them.

Outlines
00:00
📚 Derivatives of Trigonometric Functions

This paragraph introduces the derivatives of trigonometric functions, highlighting the six key derivatives that are essential to understand. It begins with the derivatives of sine (cosine x) and cosine (negative sine x), and then proceeds to discuss the derivatives of tangent (secant squared) and cotangent (cofunction of tangent, which is cosecant squared with a negative sign). The paragraph emphasizes the pattern and similarity between the derivatives of tan and cotan, as well as secant and cosecant. It also provides a method for determining the derivatives of expressions involving trigonometric functions through examples, demonstrating how to apply the derivatives of sine, tangent, and secant to find the derivatives of more complex expressions.

05:00
📝 Summary of Trigonometric Derivatives

In this paragraph, the speaker summarizes the key points made in the previous discussion on trigonometric function derivatives. It reiterates the importance of recognizing the patterns and relationships between the derivatives of trigonometric functions, particularly the negative sign associated with cofunctions starting with 'c'. The speaker leaves the final answer of the examples provided in the previous paragraph as a reference for further study, ensuring that the audience has a clear understanding of how to derive the derivatives of trigonometric functions.

Mindmap
Keywords
💡Derivatives
Derivatives are a fundamental concept in calculus that represent the rate of change or the slope of a function at a particular point. In the context of the video, derivatives of trigonometric functions are discussed, which are essential for understanding how trigonometric functions change as their input values vary. The video provides the derivatives for various trigonometric functions, such as sine, cosine, tangent, secant, cotangent, and cosecant, and demonstrates how to apply these derivatives in solving problems.
💡Trigonometric Functions
Trigonometric functions, including sine, cosine, tangent, secant, cotangent, and cosecant, are mathematical functions that relate the angles of a right triangle to the ratios of its sides. These functions are widely used in various fields, including mathematics, physics, and engineering, to model periodic phenomena. In the video, the focus is on the derivatives of these functions, which describe how the functions change as their input (usually an angle measured in radians) varies.
💡Sine Function
The sine function is one of the six trigonometric functions and is often denoted by sin(x). It relates the ratio of the length of the side opposite an angle in a right triangle to the length of the hypotenuse. In the video, it is mentioned that the derivative of the sine function is the cosine function, which means that the rate of change of the sine function with respect to its input is given by the value of the cosine function at the same point.
💡Cosine Function
The cosine function, similar to the sine function, is a fundamental trigonometric function that relates the ratio of the length of the adjacent side to the hypotenuse in a right triangle. It is denoted by cos(x) and plays a crucial role in the video as it is the derivative of the sine function. This means that the slope of the sine curve at any point is given by the cosine of that point.
💡Tangent Function
The tangent function, denoted by tan(x), is a trigonometric function that represents the ratio of the opposite side to the adjacent side in a right triangle. In the video, it is emphasized that the derivative of the tangent function is the secant function squared, which reflects the rate of change of the tangent function in terms of the secant function.
💡Secant Function
The secant function, written as sec(x), is the reciprocal of the cosine function and represents the ratio of the hypotenuse to the adjacent side in a right triangle. In the video, it is highlighted that the derivative of the secant function is the secant function times the tangent function, indicating how the secant function changes as the angle changes.
💡Cotangent Function
The cotangent function, denoted by cot(x), is the reciprocal of the tangent function and is defined as the ratio of the adjacent side to the opposite side in a right triangle. The video points out that the derivative of the cotangent function is the negative cosecant function squared, which shows the relationship between the rate of change of the cotangent function and the cosecant function.
💡Cosecant Function
The cosecant function, written as csc(x), is the reciprocal of the sine function and represents the ratio of the hypotenuse to the opposite side in a right triangle. In the video, it is mentioned that the derivative of the cosecant function is the negative cosecant function times the cotangent function, illustrating how the cosecant function's rate of change is related to the cotangent function.
💡Derivative of Expressions
The derivative of an expression is the rate of change of that expression with respect to its variable. In the video, several examples are given on how to find the derivative of expressions involving trigonometric functions. For instance, the derivative of an expression like 5 sine x - 4 tangent x is calculated by applying the derivatives of the individual functions (5 times the derivative of sine x and -4 times the derivative of tangent x) to obtain 5 cosine x - 4 secant squared x.
💡Patterns in Derivatives
The video emphasizes the importance of recognizing patterns in the derivatives of trigonometric functions, especially for cofunctions like tangent and cotangent. It is noted that the derivatives of cofunctions starting with a 'c' (such as cotangent and cosecant) have a negative sign. Understanding these patterns can greatly simplify the process of finding derivatives and solving related problems.
💡Examples and Practice
The video provides several examples and practice problems to illustrate how to calculate the derivatives of trigonometric functions. These examples serve to reinforce the concepts discussed and help viewers understand how to apply the derivatives in practical situations. By working through these examples, viewers can gain a deeper understanding of the material and improve their problem-solving skills.
Highlights

Derivative of sine x is cosine x.

Derivative of cosine x is negative sine x.

Derivative of tangent is secant squared.

Derivative of cotangent is negative cosecant squared.

Derivative of secant is secant x tangent x.

Derivative of cosecant x is negative cosecant x cotangent x.

Cofunctions starting with 'c' have negative derivatives.

Similarities between derivatives of tan and cotan, secant and cosecant.

Derivative of an expression, five sine x minus four tangent x, is 5 cosine x minus 4 secant squared x.

Derivative of eight secant x minus five cosine x is 8 secant x tangent x plus 5 sine x.

Derivative of two cotangent x minus seven cosecant x is negative 2 cosecant squared x plus 7 cosecant x cotangent x.

Knowing the derivatives of sine, tangent, and secant helps in figuring out the other three derivatives.

The derivative of cotangent is negative cosecant squared, following the pattern of cofunctions with a 'c'.

The derivative of cosecant is negative cosecant cotangent, maintaining the negative sign pattern for cofunctions.

Understanding the derivatives of trigonometric functions is essential for solving calculus problems involving them.

The process of finding derivatives involves recognizing patterns and applying the rules of differentiation.

Transcripts

Browse More Related Video

Derivatives of Trigonometric Functions

Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial

Derivatives of Trig Functions (Sin, Cos, Tan) in Calculus - [1-4]

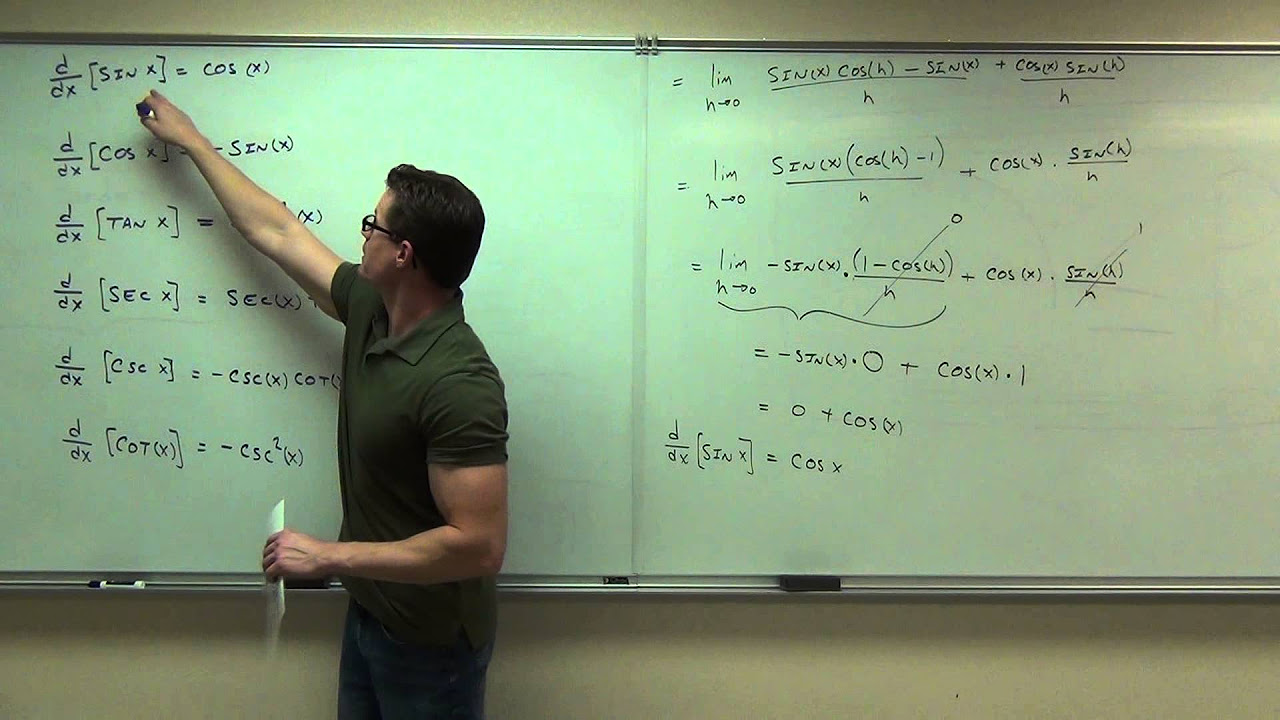
Calculus 1 Lecture 2.5: Finding Derivatives of Trigonometric Functions

Derivative of Sine and Cosine Functions | Calculus

Quotient Rule | MIT 18.01SC Single Variable Calculus, Fall 2010

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryDerivativesCalculusPatternsMath EducationSine and CosineTangent and CotangentSecant and CosecantDifferential EquationsMath Tutorial