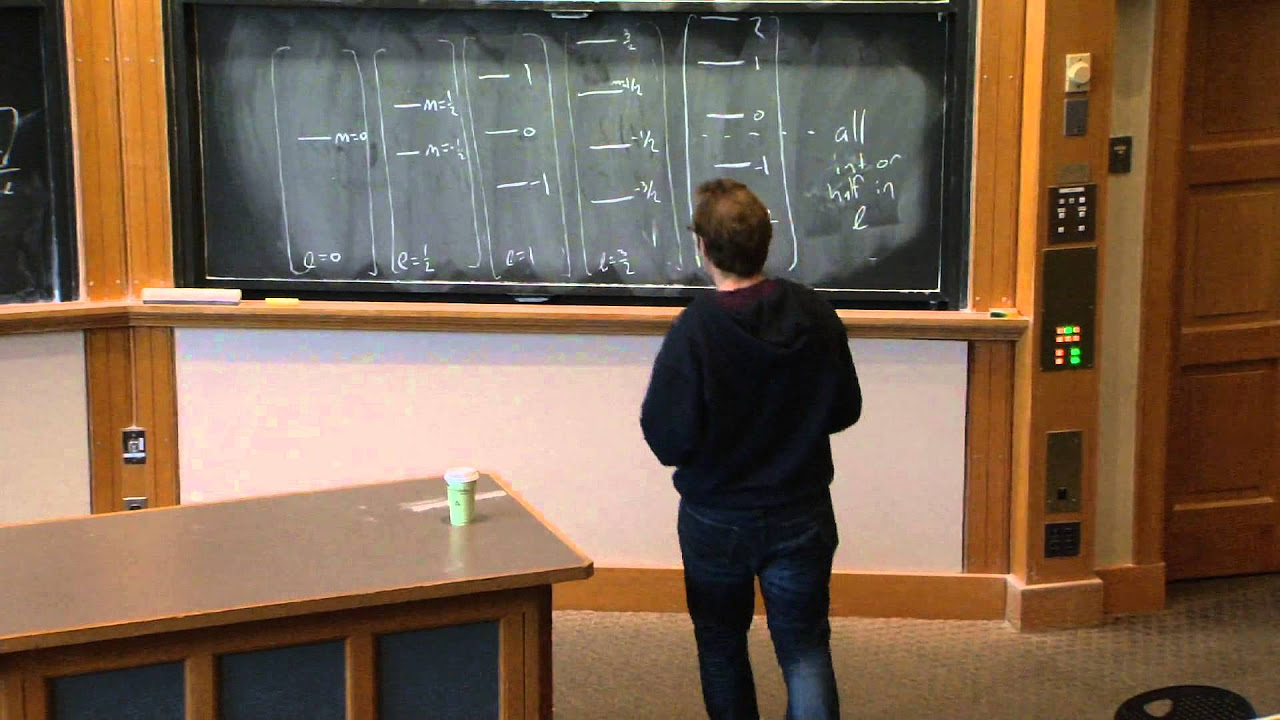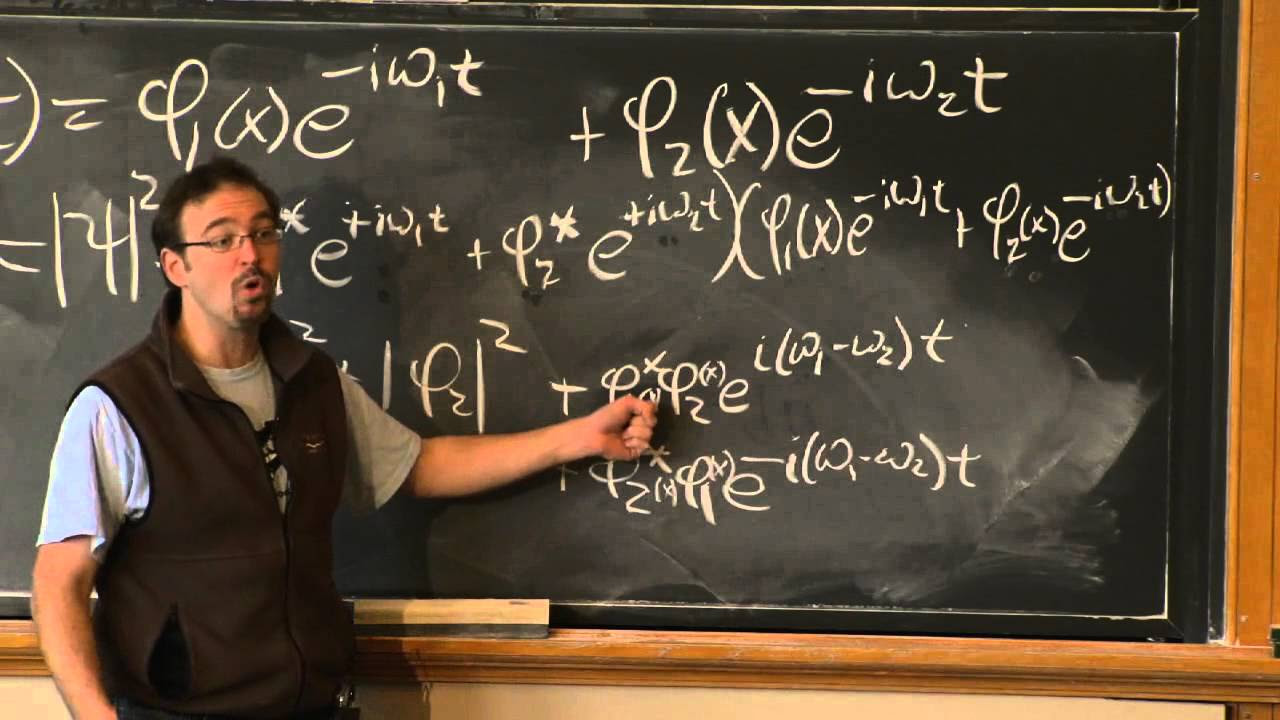Lecture 9: Operator Methods for the Harmonic Oscillator
TLDRThe lecture delves into the quantum mechanics of the harmonic oscillator, focusing on the exam preparation and the conceptual understanding of the subject matter. It explores the operator method, the significance of Hermitian operators, and the role of commutation relations in determining the energy eigenstates. The professor elucidates the concept of raising and lowering operators, demonstrating how they construct a ladder of energy states, and emphasizes the uniqueness of the harmonic oscillator's evenly spaced energy levels. The session also clarifies misconceptions about operator adjoints and observables, highlighting the importance of dimensional analysis and the physical implications of mathematical constructs.
Takeaways
- 📚 The lecture is about MIT OpenCourseWare's commitment to providing free educational resources, with an upcoming exam on the horizon and a review of the lecture material from the previous class.
- 🗓️ The exam is scheduled for a Thursday a week from the lecture, with the material from the Tuesday lecture not included in the exam content.
- 📝 The exam will consist of a mix of short questions and computations, focusing more on conceptual understanding rather than an excessive number of calculations.
- 🤔 The professor emphasizes the importance of problem sets for exam preparation, stating that only topics covered in problem sets will be on the exam, and variations of those problems may appear in a different form on the exam.
- 🔍 The lecture delves into the specifics of the harmonic oscillator problem, discussing the solutions obtained through the series method and the implications of boundary conditions on those solutions.
- 🧩 The professor explains the subtleties involved in the series expansion of the harmonic oscillator and the importance of choosing the convergent solution to avoid divergence issues.
- 🌟 The lecture highlights the evenly spaced energy levels of the quantum harmonic oscillator and introduces the operator method as a way to understand and re-derive these results without brute force calculations.
- 📈 The operator method involves using the energy operator for the harmonic oscillator and performing dimensional analysis to simplify the problem and reveal the underlying physics.
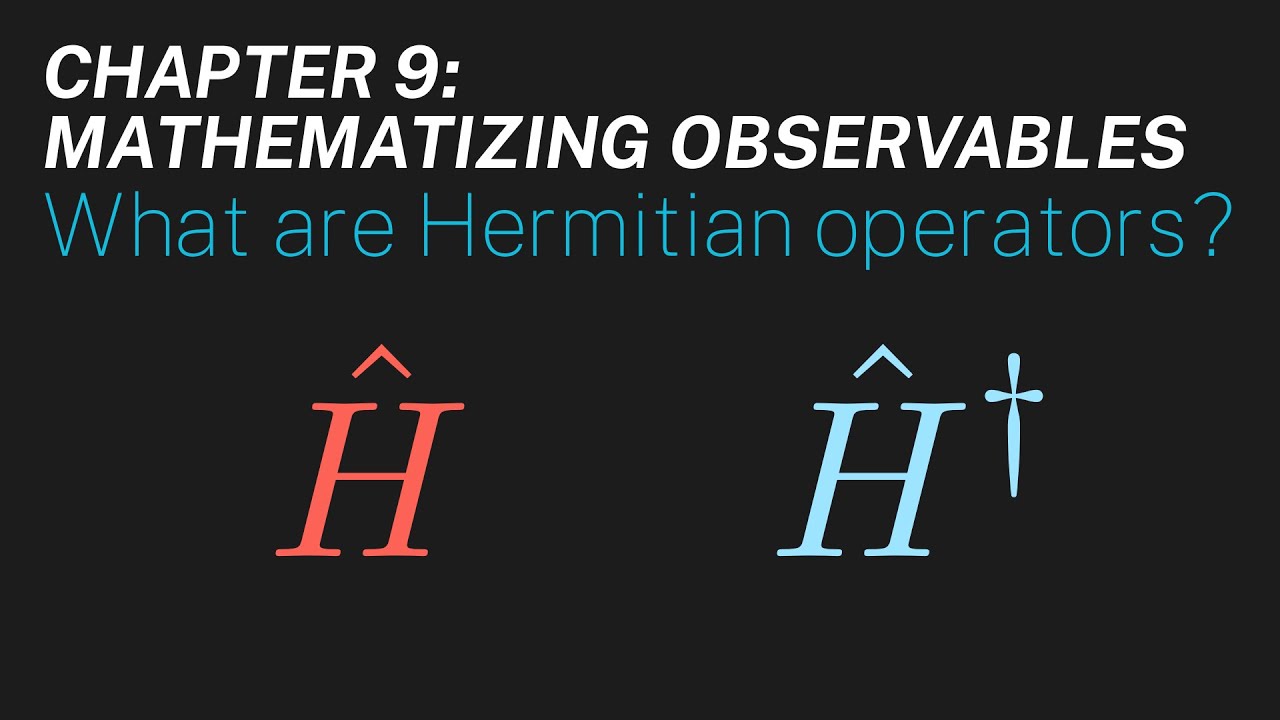
- 🔢 The importance of Hermitian operators in quantum mechanics is discussed, with the professor explaining that Hermitian operators have real eigenvalues and are associated with observable physical quantities.
- 🔄 The lecture introduces the concept of adjoints of operators, showing through examples how to determine the adjoint and its significance in the context of Hermitian operators.
- 🔑 The 'a' and 'a dagger' operators are defined as the lowering and raising operators, respectively, which shift the energy levels of the system by a fixed amount, revealing the structure of the energy spectrum.
Q & A
What is the main purpose of the exams in this MIT course as described by the professor?
-The main purpose of the exams is not to give students a grade but to provide feedback on their understanding of quantum mechanics, ensuring they have a solid grasp of the concepts rather than just superficially thinking they understand.
What is the exam format according to the professor's explanation?
-The exam will be a combination of short questions and computations, focusing more on conceptual understanding rather than an enormous number of computations, with a few calculations included.
What is the significance of the problem sets in relation to the exam?
-The problem sets are part of the exam preparation, and anything that has been on a problem set is fair game for the exam. However, topics not covered on a problem set will not be tested.
What is the professor's approach to exam questions based on the problems students have practiced?
-The professor will take problems and ideas that students have studied before and slightly modify them to make students think through them in real time on the exam, ensuring they understand the concepts deeply.
What is the topic of the audience's first question about the exam, and what does the professor clarify?
-The audience asks about the exam, and the professor clarifies that it will be on Thursday a week hence, covering all material through today's lecture, including problems that should be posted after the lecture.
What is the main topic of the lecture following the exam discussion?
-The main topic of the lecture is the analysis of the quantum harmonic oscillator, specifically focusing on why the energy eigenvalues are evenly spaced and introducing the operator method to re-derive these results.
What is the significance of the evenly spaced energy eigenvalues in the quantum harmonic oscillator?
-The evenly spaced energy eigenvalues are a surprising feature of the quantum harmonic oscillator, indicating a deeper underlying structure that the lecture aims to explain.
What mathematical tool does the professor introduce to explain the structure of the quantum harmonic oscillator?
-The professor introduces the operator method, which is a powerful tool in quantum mechanics for analyzing systems and has an independent life in mathematics, particularly in algebra.
What is the role of dimensional analysis in the context of the energy operator for the harmonic oscillator?
-Dimensional analysis helps to identify the salient scales in the problem and make the equations dimensionless, simplifying the analysis and ensuring that the solutions are expressed in terms of the correct units.
What is the significance of the operator method in understanding the energy eigenvalues of the quantum harmonic oscillator?
-The operator method reveals the commutation relations between operators, which in turn explain the evenly spaced energy eigenvalues of the quantum harmonic oscillator without the need for brute force calculations.
What is the professor's explanation for the evenly spaced energy levels in the quantum harmonic oscillator?
-The professor explains that the evenly spaced energy levels are a result of the commutation relations between the lowering and raising operators, a and a dagger, and the energy operator E.
What is the role of the operator 'a' in the quantum harmonic oscillator?
-The operator 'a' is the lowering operator, which when acting on an energy eigenstate, decreases the energy by h bar omega, effectively moving to the next lower state in the energy ladder.
What is the role of the operator 'a dagger' in the quantum harmonic oscillator?
-The operator 'a dagger' is the raising operator, which when acting on an energy eigenstate, increases the energy by h bar omega, effectively moving to the next higher state in the energy ladder.
What is the minimum energy state of the quantum harmonic oscillator called, and why can't the energy go lower than this state?
-The minimum energy state is called the ground state. The energy cannot go lower than this state because further application of the lowering operator 'a' on the ground state results in zero, indicating there are no lower energy states.
How does the professor ensure that there are no intersecting energy ladders in the quantum harmonic oscillator?
-The professor uses the commutation relations and the properties of the lowering operator 'a' to show that all energy states must be part of a single, non-intersecting ladder. Any attempt to create a separate ladder would result in degeneracies, which are not possible in one-dimensional bound state systems.
What is the physical interpretation of the operators 'a' and 'a dagger' in terms of observables?
-The operators 'a' and 'a dagger' are not observables themselves, but they are related to observables in meaningful ways. They represent the actions of lowering and raising the energy states, respectively, and are fundamental in the construction of the energy ladder in the quantum harmonic oscillator.
How does the professor use the commutators to derive the energy eigenvalues without solving differential equations?
-The professor uses the commutators of the energy operator E with the lowering and raising operators 'a' and 'a dagger' to derive the relationship between the energy eigenvalues. By acting with these operators on the energy eigenstates, he shows that the energy eigenvalues form a ladder with evenly spaced intervals of h bar omega.
What is the significance of the Gaussian function in the context of the quantum harmonic oscillator's ground state?
-The Gaussian function represents the ground state wave function of the quantum harmonic oscillator. It is derived from the condition that the lowering operator 'a' acting on the ground state results in zero, leading to a first-order differential equation with the Gaussian as its solution.
How are the Hermite polynomials related to the energy eigenstates of the quantum harmonic oscillator?
-The Hermite polynomials are used to construct the energy eigenstates of the quantum harmonic oscillator. They appear as factors in the wave functions of the excited states, which are obtained by applying the raising operator 'a dagger' to the ground state multiple times.
Outlines
📚 Introduction to MIT OpenCourseWare and Exam Details
The script begins with an introduction to MIT OpenCourseWare, highlighting its commitment to providing free, high-quality educational resources, with a call to support the initiative by visiting ocw.mit.edu. The professor then addresses the audience, discussing an upcoming exam, clarifying that the material from the next lecture will not be on the exam but emphasizing the importance of the exam as a review of all previously covered topics. The exam will include a mix of conceptual questions and some calculations, focusing more on understanding than computation. The professor also mentions that practice problems will be posted and discusses the strategy for exam preparation, including the relationship between problem sets and exam content.
🔍 In-Depth Discussion on Exam Preparation and Quantum Mechanics
The conversation shifts to exam preparation strategies and the philosophy behind the exams, with the professor expressing indifference towards grades and focusing on providing feedback for understanding. The discussion then moves to quantum mechanics, specifically the harmonic oscillator problem addressed in a previous lecture. The professor delves into the series method used to solve the problem, explaining the presence of two solutions and the role of boundary conditions. The explanation includes an exploration of the second-order differential equation and the integration constants, highlighting the suppression of a singular solution and the focus on a convergent solution.
🌟 The Operator Method and Dimensional Analysis
The professor introduces the operator method for analyzing quantum systems, starting with a review of the energy operator for a harmonic oscillator. The importance of dimensional analysis is stressed, with an explanation of how to identify relevant scales in a problem and make equations dimensionless. Using the parameters of the problem, the professor constructs characteristic scales and redefines the energy operator in terms of these scales, setting the stage for a deeper exploration of the quantum harmonic oscillator.
📝 Factoring the Energy Operator and Introducing the Adjoint
The script continues with an attempt to factor the energy operator, leading to a discussion about the sum of squares and the temptation to factorize. The professor introduces the concept of the adjoint of an operator, explaining how it is defined through the inner product and providing a mathematical definition. The script includes examples of finding adjoints for different operators, emphasizing the importance of the adjoint in quantum mechanics.
🤔 Exploring the Adjoint of Complex Numbers and Derivatives
This paragraph delves into the adjoint properties of complex numbers and the derivative operator. It demonstrates that the adjoint of a complex number is its complex conjugate and that the adjoint of the derivative operator is minus the derivative operator, given certain boundary conditions. The professor also discusses the implications of these findings for different sets of functions and the importance of normalizable functions in physics.
🔧 Hermetian Operators and Their Properties
The concept of Hermetian operators is introduced, defined as operators that are equal to their own adjoint. The professor explains that Hermetian operators have real eigenvalues and that any operator corresponding to a physical observable must be Hermetian. Examples of Hermetian operators, including the position operator, are provided, and the professor emphasizes the significance of Hermetian operators in representing observables in quantum mechanics.
🚀 The Role of Non-Hermetian Operators in Quantum Mechanics
The script explores the role of non-Hermetian operators in quantum mechanics, particularly the operators 'a' and 'a dagger,' which do not represent observables but are crucial for the structure of the theory. The professor discusses the commutation relation between 'a' and 'a dagger,' which is fundamental to understanding the energy levels of the harmonic oscillator. The paragraph also touches on the existence of eigenvectors for non-Hermetian operators and their implications in the context of quantum mechanics.
🌐 Commutators and Their Implications for Energy Levels
The professor discusses the implications of commutators for the energy levels of a system, showing how the energy operator 'E' can be related to the lowering operator 'a' through commutators. The script demonstrates that applying 'a' to an energy eigenstate results in a new state with a lower energy, establishing a connection between the commutator and the energy level structure. The professor also introduces the concept of 'a' as a lowering operator and highlights the power of using commutators in quantum mechanics.
🔄 The Ladder of Energy States and Its Characteristics
This paragraph explores the concept of a ladder of energy states, constructed using the lowering and raising operators 'a' and 'a dagger.' The professor explains how these operators can be used to move up and down the energy ladder, with each step representing an increase or decrease in energy by a fixed amount. The script also addresses the question of whether the ladder can extend infinitely in both directions and introduces the idea of a ground state that cannot be lowered further.
🏁 The Ground State and Termination of the Energy Ladder
The professor discusses the termination of the energy ladder at the ground state, explaining that the ladder cannot extend infinitely downward due to the positive definite nature of the energy operator. The script explores the concept of the ground state as the lowest energy state that cannot be annihilated further by the lowering operator 'a.' The professor also addresses the question of whether there could be additional states not on the main ladder, concluding that there cannot be intersecting ladders due to the non-degeneracy of energy levels in one-dimensional systems.
🎯 Deriving the Wave Functions from Commutators
The script concludes with a demonstration of how the wave functions of the harmonic oscillator can be derived from the commutation relations, without solving differential equations. The professor shows that the ground state wave function is a Gaussian and that the excited states can be obtained by applying the raising operator, which involves taking derivatives of the ground state wave function. This approach is presented as an efficient method for constructing the wave functions and understanding the energy spectrum of the harmonic oscillator.
Mindmap
Keywords
💡Creative Commons license
💡MIT OpenCourseWare
💡Exam
💡Problem set
💡Quantum mechanics
💡Harmonic oscillator
💡Differential equation
💡Asymptotic analysis
💡Hermitian adjoint
💡Observable
💡Commutator
💡Ladder operators
💡Ground state
💡Normalization
💡Hermit polynomials
Highlights
Introduction to the importance of MIT OpenCourseWare and its reliance on donations for high-quality educational resources.
Announcement of an upcoming exam with a focus on conceptual understanding rather than extensive computations.
Clarification that the material covered on Tuesday will not be on the exam, emphasizing review of prior lectures.
Discussion on the structure of the exam, including a mix of short questions and computations with a focus on conceptual problems.
The professor's commitment to posting practice problems to aid in exam preparation.
Details on a problem set due the following Tuesday, which is integral to exam preparation.
Explanation of the exam strategy where problem sets dictate what will be on the exam, ensuring fairness.
The professor's perspective on exams as a tool for feedback on understanding rather than just grading.
An in-depth question-and-answer session on the harmonic oscillator and its solutions, highlighting the importance of boundary conditions.
Discussion on the uniqueness and non-existence of certain solutions in the harmonic oscillator problem due to asymptotic behavior.
The revelation of the evenly spaced energy levels in the quantum harmonic oscillator and the mystery behind this phenomenon.
Introduction to the operator method as an alternative approach to solving quantum mechanical systems.
Dimensional analysis of the energy operator for the harmonic oscillator and the significance of the link scales.
The exploration of the operator method's connection to algebra in mathematics and its applications beyond quantum mechanics.
Explanation of the energy operator in terms of the sum of squares and the attempt to factor it using operators.
Introduction and definition of the adjoint operator and its importance in quantum mechanics.
Examples of finding the adjoint of various operators, emphasizing the mathematical process and its physical implications.
The concept of Hermitian operators and their significance in representing physical observables with real eigenvalues.
Discussion on the lowering and raising operators, a, and a dagger, and their role in constructing the energy ladder.
The derivation of the energy eigenstates and the understanding that the energy ladder is evenly spaced without solving differential equations.
The ground state's unique property of being annihilated by the lowering operator and its role in terminating the energy ladder.
The proof that there cannot be intersecting or missed energy ladders due to the lack of degeneracies in one-dimensional systems.
The connection between the commutation relations and the structure of energy eigenvalues in various quantum systems.
Efficient construction of higher energy states using derivatives and the raising operator instead of solving differential equations.
The upcoming review session to reinforce the concepts covered and its aim to support students in their exam preparation.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: