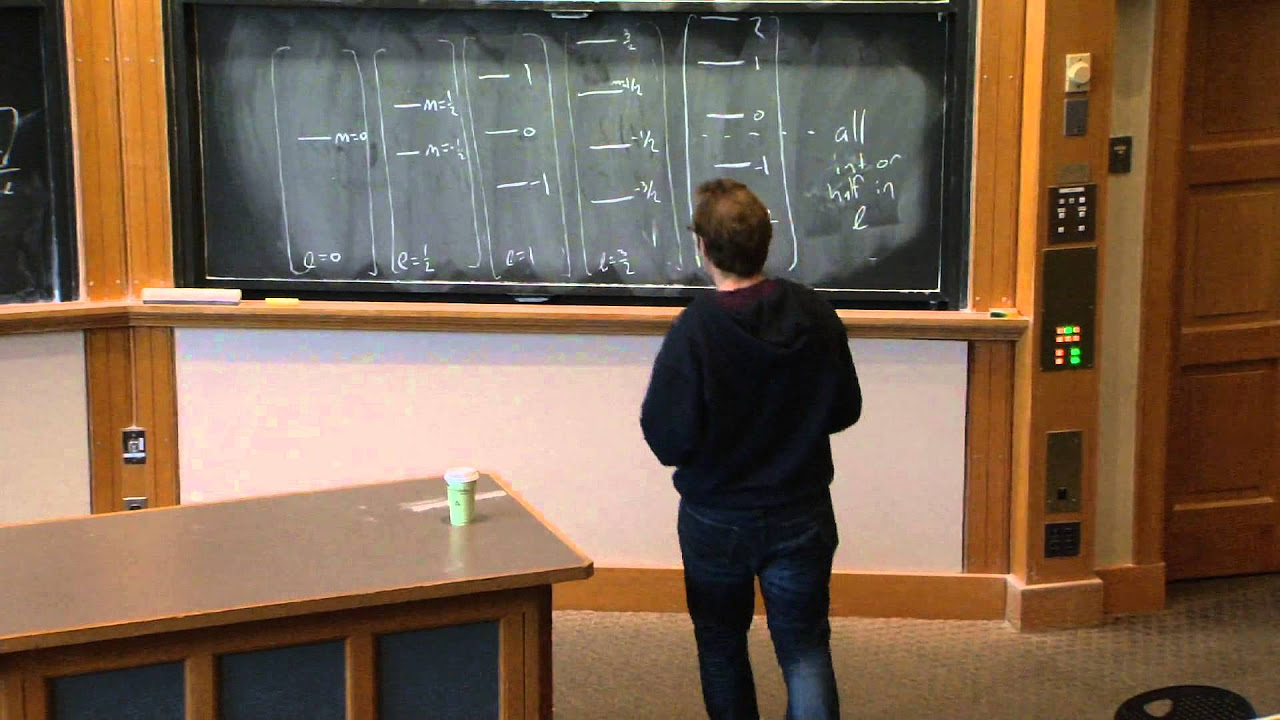Lecture 15: Eigenstates of the Angular Momentum Part 1
TLDRThe lecture delves into the quantum mechanics of angular momentum, emphasizing the significance of symmetries and degeneracies. It explores the connection between symmetries and conservation laws, particularly rotational invariance and its impact on energy levels. The professor introduces the angular momentum operators, Lx, Ly, Lz, and their commutation relations, highlighting the impossibility of simultaneous eigenfunctions for non-commuting operators. The lecture culminates in the concept of ladder operators, L+ and L-, which facilitate the analysis of eigenfunctions for L² and Lz, setting the stage for further exploration in the next session.
Takeaways
- 📚 The lecture discusses the importance of MIT OpenCourseWare for providing free educational resources and mentions an upcoming midterm exam and problem set due dates.
- 📅 The professor informs students about an exam on the 18th and a problem set that will be posted and due the following week, with adjustments made for a holiday.
- 📝 The format of the exam is described as a mix of short answers and computations, with a practice exam to be released for additional preparation.
- 🔍 The professor emphasizes the correlation between doing well on problem sets and exams and suggests using resources like Stellar and OCW for practice.
- 🤔 A student asks if the exam will cover all material, and the professor confirms that it is cumulative, requiring knowledge from the entire semester.
- 🔬 The lecture explores the implications of certain operators and their commutators on the system's energy eigenvalues and eigenfunctions, highlighting the role of symmetries and degeneracies in quantum mechanics.
- 🌌 The concept of angular momentum in quantum mechanics is introduced, with the professor explaining its significance and how it relates to symmetries and degeneracies.
- 🔍 The professor derives the quantum mechanical operators for angular momentum and discusses their properties, including their commutation relations.
- 📈 The lecture touches on the concept of complete sets of commuting observables and how they relate to specifying the state of a quantum system.
- 🧩 The professor introduces 'L plus' and 'L minus' operators, which are used to construct the eigenfunctions of the angular momentum operators through ladder operations.
- 🔑 The commutation relations between Lz, L plus, and L minus are highlighted as key to understanding the structure of angular momentum eigenfunctions.
Q & A
What is the purpose of the content provided in the transcript?
-The content is a lecture transcript discussing various quantum mechanics concepts, including problem sets, exams, and the principles of angular momentum and degeneracy in quantum systems.
What is the significance of the Creative Commons license mentioned in the transcript?
-The Creative Commons license indicates that the content is freely available and can be shared and adapted under certain conditions, supporting the mission of MIT OpenCourseWare to offer high-quality educational resources.
What is the next step for students after the midterm exam mentioned in the transcript?
-The next step for students is to complete a problem set that will be posted and is due the following week, with the due date adjusted for a holiday.
Why is the format of the upcoming exam described as 'canonical' in the transcript?
-The format is described as 'canonical' because it will consist of a series of short answer questions and computations, similar to the level of problem sets and a practice exam that will be provided.
What is the recommendation for students preparing for the exam in the transcript?
-The recommendation is for students to attempt the practice exam under time constraints to gauge their preparedness and to use additional resources such as previous problem sets and exams available on Stellar and OCW.
What does the professor imply about the relationship between studying problem sets and exam performance?
-The professor implies a strong correlation between success on exams and thorough engagement with problem sets, suggesting that students who work through problems diligently will be more confident and perform better.
Why does the professor emphasize the importance of understanding separable equations in the transcript?
-The professor emphasizes this because separable equations are a key technique in solving quantum mechanics problems, especially when dealing with systems in three dimensions.
What is the significance of the degeneracy observed in the 3D harmonic oscillator as discussed in the transcript?
-The degeneracy in the 3D harmonic oscillator is significant because it demonstrates that bound states in three dimensions can exhibit degeneracy due to the system's symmetry, unlike in one dimension.
What is the role of symmetry in the context of degeneracy as mentioned in the transcript?
-Symmetry plays a crucial role in the occurrence of degeneracy. When a system possesses symmetry, such as rotational invariance, it can lead to degenerate energy levels, meaning multiple states with the same energy.
Why does the professor suggest that the eigenfunctions of Lz must be single-valued?
-The eigenfunctions of Lz must be single-valued to ensure that the wave function remains consistent under a full rotation (2π change in the angle φ), which is a requirement in quantum mechanics for the physical interpretation of the wave function.
What is the implication of the commutation relations of the angular momentum operators as discussed in the transcript?
-The commutation relations imply that certain operators cannot have simultaneous eigenfunctions, which in turn affects the possible measurements that can be precisely determined at the same time, reflecting the Heisenberg uncertainty principle.
What does the professor mean by 'complete set of commuting observables' in the context of angular momentum?
-A complete set of commuting observables refers to a group of operators that all commute with each other and whose eigenvalues are sufficient to uniquely determine the state of a quantum system. For angular momentum, this set includes Lz and L squared.
Why are L plus and L minus operators introduced in the discussion of angular momentum?
-L plus and L minus operators are introduced as a way to exploit the commutation relations of the angular momentum operators, allowing for the raising and lowering of eigenvalues in a manner similar to the harmonic oscillator, thus simplifying the analysis of the eigenfunctions.
Outlines
📚 Course Updates and Study Tips
The professor begins by acknowledging the support of the audience, emphasizing the importance of donations for the continuation of MIT OpenCourseWare. The audience is informed about the upcoming midterm and the posting of a problem set with a revised due date. The professor suggests using the problem set as a review for the exam and highlights the format of the exam, which will consist of short answers and computations similar to the problem sets. A practice exam will be made available, and the professor recommends using it within a time constraint to gauge readiness. The connection between problem-solving practice and exam performance is stressed, and additional resources on OCW are suggested for further study. The professor also addresses a question about the exam's scope, confirming it will cover the entire semester's material.
🔍 Quantum Mechanics Review and Commutator Insights
The session continues with a review of quantum mechanics concepts, focusing on the implications of commutator relationships between energy and other operators. The professor explains how certain commutation relations indicate a ladder structure in the energy spectrum, allowing for the prediction of evenly spaced energy levels. The discussion then shifts to operators that commute with the energy operator, leading to the existence of simultaneous eigenfunctions and the possibility of multiple states sharing the same energy eigenvalue. The professor uses the example of a free particle to illustrate these concepts and contrasts it with the harmonic oscillator, which lacks such degeneracy due to its non-commutative nature with momentum. The lecture wraps up with a deeper dive into the meaning of eigenfunctions being complete and the relationship between complete bases and degeneracy in energy levels.
🚀 Transition to Higher Dimensions and Unitary Operators
The lecture progresses to the exploration of quantum mechanics in higher dimensions, starting with a transition from a one-dimensional tricycle to a three-dimensional Yamaha, highlighting the persistence of fundamental dynamics. The conversation centers on the impact of dimensions on the principles discussed earlier, particularly the effect on the commutation relations and the potential changes in the understanding of quantum systems. The professor also introduces the concept of unitary operators and their relationship with energy operators, emphasizing the role of symmetries in the form of unitary transformations. Examples of translation and time evolution operators are given, and the connection between symmetries, conserved quantities, and the associated Hermitian operators is established.
🌌 Quantum Mechanics in 3D: Position, Momentum, and Uncertainty
The professor delves into the specifics of quantum mechanics in three dimensions, discussing the energy operator and its relation to position and momentum. The non-commutative nature of position and momentum operators is highlighted, leading to the uncertainty principle. The lecture explains that while position and momentum operators for different dimensions commute with each other, they do not share simultaneous eigenfunctions due to the uncertainty principle. The professor also introduces the concept of the Schrödinger equation in 3D, using vector notation and gradient operators to describe the wave function's time evolution. The importance of choosing appropriate coordinate systems for problem-solving is underscored, with a promise to explore the Laplacian in various coordinate systems.
🌟 Free Particle in 3D: Energy Eigenfunctions and Superposition
The lecture focuses on the free particle in three dimensions, starting with the construction of energy eigenfunctions using the Schrödinger equation. The professor demonstrates the separability of the equation and constructs solutions in Cartesian coordinates. The solutions are expressed as products of one-dimensional wave functions, reflecting the particle's momentum in each direction. The concept of superposition is introduced to account for all possible momentum directions, leading to the understanding that not all solutions are of the simple product form assumed initially. The lecture concludes with a discussion about the normalizability of the wave functions and the implications of choosing oscillating solutions for the eigenfunctions.
🔄 Degeneracy and Symmetry in Quantum Systems
The professor explores the concept of degeneracy in quantum systems, particularly in the context of a free particle in three dimensions. The discussion revolves around the infinite number of directions a particle can move in, each with the same energy, leading to a vast degeneracy of energy eigenfunctions. The lecture emphasizes the role of symmetry in causing degeneracies, as the system's invariance under rotation allows for states with the same energy but different momenta. The professor also contrasts this with the non-degenerate bound states in one dimension and sets the stage for examining the 3D harmonic oscillator to further investigate degeneracy in bound systems.
🎻 3D Harmonic Oscillator and Degeneracy Analysis
The lecture continues with an analysis of the 3D harmonic oscillator, focusing on the separability of the energy eigenvalue equation and its similarity to the 1D harmonic oscillator problem. The professor constructs the energy eigenfunctions by taking products of one-dimensional harmonic oscillator eigenfunctions for each spatial dimension. The energy levels are expressed as sums of the individual dimension's energy contributions. The discussion then turns to the degeneracy of these energy levels, highlighting the presence of degeneracies even in bound states in three dimensions. The professor illustrates this with examples of different excitation numbers and their corresponding energies, showing that states with different excitation patterns can share the same energy.
🔢 Degeneracy Patterns and Number Theory
The professor investigates the pattern of degeneracies in the 3D harmonic oscillator, noting the increase in degeneracy with energy levels. The audience suggests a connection to number theory, prompting the professor to discuss the degeneracy numbers for various energy levels. A formula for the degeneracy is proposed, which is confirmed to hold for the given examples. The lecture emphasizes the deep connection between symmetries and degeneracies, explaining that degeneracies arise due to the system's rotational symmetry. The professor also points out that without symmetry, degeneracies would not exist, and that the presence of degeneracies can hint at underlying symmetries in the system.
🌀 Angular Momentum and Rotational Symmetry
The lecture concludes with an introduction to angular momentum, prompted by the discussion of rotational symmetry and its connection to degeneracy. The professor outlines the plan to study rotations and their generators, the angular momentum operators, in the following lectures. The audience's question about the symmetry explaining the growth of degeneracy is acknowledged, and the professor agrees to address it later. The importance of angular momentum and its addition in quantum mechanics is highlighted, with the professor sharing his realization of its significance in the field.
⚙️ Derivation of Angular Momentum Operators
The professor begins by defining the angular momentum operator in quantum mechanics, drawing an analogy with its classical counterpart. The components of the angular momentum operator are derived, and concerns about operator ordering are addressed. The lecture continues with the expression of these operators in Cartesian and spherical coordinates, highlighting the simplicity of the Lz operator in spherical coordinates. The professor also introduces the concept of angular momentum squared and its significance in the Hamiltonian. The dimensions of angular momentum and the role of h bar as a dimensionless constant are discussed, leading to an exploration of the eigenfunctions of the angular momentum operators.
🔄 Commutators and Angular Momentum Eigenfunctions
The lecture delves into the commutators of the angular momentum operators, revealing their simplicity despite initial complexity. The professor demonstrates the calculation of the commutator between Lx and Ly, leading to the discovery that the commutators cycle through the components of angular momentum. The implications of these commutators for the eigenfunctions of the angular momentum operators are discussed, highlighting the inability to find simultaneous eigenfunctions for Lx and Ly due to their non-commutative nature. However, the existence of simultaneous eigenfunctions for Lx (or Ly or Lz) and L squared is confirmed, setting the stage for further exploration of the angular momentum system.
🎓 Complete Set of Commuting Observables and Angular Momentum
The professor introduces the concept of a complete set of commuting observables, necessary to fully specify the state of a quantum system. The discussion revolves around the criteria for a set of operators to be considered complete, emphasizing that they must all commute with each other and that their eigenvalues must uniquely identify the system's state. The lecture applies this concept to the angular momentum system, identifying Lz and L squared as a complete set of commuting observables for angular momentum. The professor also addresses a question about the commutativity of L squared and Lx, attributing it to a brute force computation that students will perform in their problem set.
🛤️ Ladder Operators and Angular Momentum Eigenfunctions
The lecture introduces ladder operators L plus and L minus, constructed from Lx and Ly, and explores their commutators with Lz and L squared. The professor
Mindmap
Keywords
💡Creative Commons license
💡MIT OpenCourseWare
💡Midterm exam
💡Problem set
💡Canonical format
💡Cumulative topic
💡Commutator
💡Eigenfunctions
💡Unitary operator
💡Schrodinger equation
💡Separable equation
💡Degeneracy
💡Angular momentum operator
💡Complete set of commuting observables
Highlights
MIT OpenCourseWare's mission to provide free, high-quality educational resources is supported by donations.
Upcoming midterm exam details, including the date and format, were announced.
A problem set will be posted and is due the following week, with a special note on the holiday adjustment of the deadline.
The importance of the problem set as part of the exam review process was emphasized.
The exam format will include short answers and computations similar to the problem sets.
A practice exam will be available, with a note on its length and intellectual difficulty compared to the actual exam.
The correlation between mastering problem sets, practicing exams, and exam performance was discussed.
Resources on Stellar and OCW for additional practice materials were mentioned.
The exam will cover cumulative topics from the entire semester.
The significance of the commutator of the energy operator with another operator and its implications on the energy spectrum was explained.
The concept of simultaneous eigenfunctions and the conditions under which they exist was explored.
The role of unitary operators in representing symmetries and their connection to conserved quantities was discussed.
The transition to 3D quantum mechanics and the implications for the energy operator and wave function were outlined.
The properties of the Laplacian operator in different coordinate systems were highlighted.
The solution to the energy eigenvalue equation for a free particle in 3D and the concept of plane waves were presented.
The degeneracy of energy eigenfunctions in 3D systems and its relation to symmetry was explained.
The example of the 3D harmonic oscillator was used to illustrate the presence of degeneracies in bound states.
The concept of angular momentum operators and their derivation from classical mechanics was introduced.
The commutation relations of angular momentum components and their implications for the eigenfunctions were discussed.
The idea of a complete set of commuting observables and its importance in quantum mechanics was explained.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: