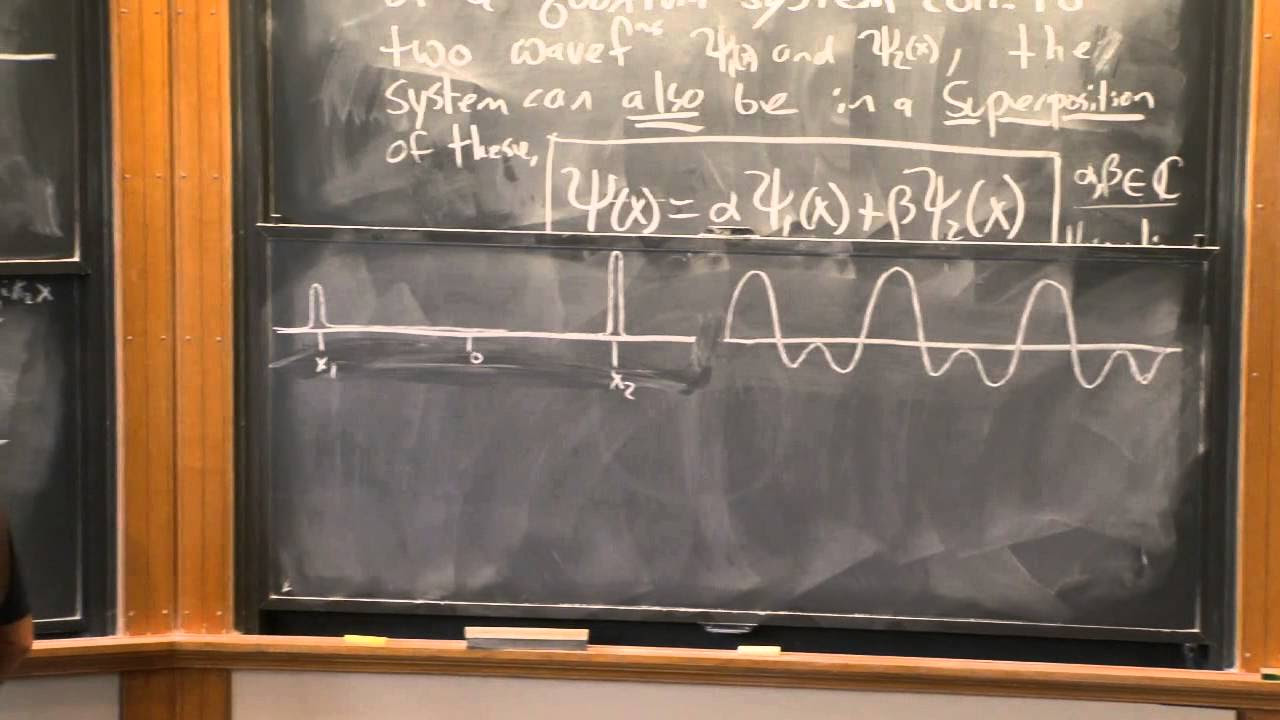17.7 Feynman Quantum Path Integrals I
TLDRThis lecture delves into Feynman's quantum path integral formulation of quantum mechanics, a complex yet fascinating topic foundational to field theory and quantum chromodynamics (QCD). It explores the connection between classical mechanics and quantum mechanics through the concept of action and the least action principle. Feynman's approach suggests that the wave function at a point is a sum of all possible paths connecting two points in space-time, each with its probability. The lecture also discusses the challenge of calculating quantum mechanical properties using the path integral method, introducing Wick rotation and its significance in evaluating the Green's function for long imaginary times.
Takeaways
- 🌟 Feynman's quantum path integral formulation of quantum mechanics is a complex and subtle topic, but it offers a new perspective and is foundational for field theory and quantum chromodynamics (QCD).
- 🔬 The formulation connects quantum mechanics to classical mechanics by generalizing the concept of a classical trajectory and considering all possible paths a particle can take.
- 📚 Quantum mechanics traditionally deals with waves and probability distributions, whereas Feynman's approach integrates these with the concept of action from classical mechanics.
- 🔗 Hamilton's principle, which states that the action is an extremum for the classical trajectory, is a key component in Feynman's path integral formulation.
- 🌐 The path integral formulation involves summing over all possible paths from point A to point B, each associated with a different probability, weighted by the action.
- 🌌 The Green's function, or propagator, is central to the path integral approach, representing the probability amplitude for a particle to move from one point to another.
- 📉 The action is minimized along the classical trajectory, and quantum mechanically, paths near this trajectory contribute significantly due to the small value of the action divided by Planck's constant.
- 📈 The path integral can be calculated using a complete set of eigenstates from quantum mechanics, relating the Green's function to the sum over all states.
- 🤔 The challenge in applying the path integral formulation is finding a practical way to calculate the wave function from the Green's function, especially for complex systems.
- ⏱ Wick rotation, which involves evaluating the Green's function for imaginary time, simplifies the calculation by turning oscillatory exponentials into decaying exponentials, emphasizing the ground state contribution.
- 🛠 The final step involves using the long-time limit of the Green's function to determine the wave function, which is crucial for performing quantum mechanical calculations.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is Feynman's quantum path integral formulation of quantum mechanics, which is a complex and subtle subject that provides a new perspective on quantum mechanics and is foundational to field theory and quantum chromodynamics (QCD).
Why is Feynman's quantum path integral formulation considered difficult?
-Feynman's quantum path integral formulation is considered difficult because it involves a deep and abstract concept of summing over all possible paths a particle can take, which is a significant departure from classical mechanics and requires a sophisticated mathematical framework to understand and apply.
What is the connection between classical mechanics and quantum mechanics as discussed in the script?
-The connection between classical mechanics and quantum mechanics discussed in the script is the idea of generalizing the classical trajectory to quantum mechanics. In classical mechanics, there is a unique trajectory for a particle given initial conditions, whereas in quantum mechanics, the particle is described by a wave function that results from summing over all possible paths, as suggested by Feynman's path integral formulation.
What role did Dirac play in influencing Feynman's approach to quantum mechanics?
-Dirac, who made significant contributions to theoretical physics, gave Feynman a hint to consider Hamilton's least action principle when thinking about quantum mechanics. This hint led Feynman to develop his path integral formulation.
What is Hamilton's least action principle and why is it significant?
-Hamilton's least action principle states that the path taken by a particle in classical mechanics is such that the action, which is the integral of the Lagrangian along the path, is an extremum (usually a minimum). It is significant because it is a fundamental principle in physics from which classical mechanics, Einstein's general theory of relativity, and optics can be derived.
What is the propagator in quantum mechanics and why is it important?
-The propagator, also known as the Green's function in quantum mechanics, is a function that describes the probability amplitude for a particle to move from one point in space to another over time. It is important because it allows for the calculation of the wave function at a later time based on the wave function at an earlier time.
How does the script relate the concept of action in classical mechanics to quantum mechanics?
-The script relates the action in classical mechanics to quantum mechanics by showing that the Green's function for a free particle is related to the action of a free particle. The action is used in the path integral formulation, where the probability amplitude for each path is given by the exponentiation of the classical action divided by the reduced Planck constant.
What is the significance of the reduced Planck constant (ħ) in the path integral formulation?
-The reduced Planck constant (ħ) plays a crucial role in the path integral formulation because it determines the weight of each path in the sum. Paths that deviate significantly from the classical path, which has the extremum of the action, will have a very small contribution to the sum due to the rapid oscillation of the exponential term in the integrand, making the paths with lower action more probable.
What is the Wick rotation mentioned in the script and how does it simplify the calculation of the Green's function?
-The Wick rotation is a method where the time variable in the Green's function is analytically continued into the imaginary plane. This rotation changes the oscillatory exponentials in the expression for the Green's function into decaying exponentials, which simplifies the calculation, especially at long imaginary times where only the ground state contributes significantly to the sum.
How does the script connect the Green's function to the wave function in quantum mechanics?
-The script connects the Green's function to the wave function by showing that the wave function at a particular point in space and time can be obtained by summing over all possible initial states, each weighted by its contribution from the Green's function. This is done by using the eigenstates of the Hamiltonian operator to express the time-dependent wave function.
Outlines
📚 Introduction to Feynman's Quantum Path Integral
This paragraph introduces the topic of Feynman's quantum path integral formulation of quantum mechanics, which is considered a challenging and subtle subject. The lecturer emphasizes its importance and fascination, stating that it provides a new perspective on quantum mechanics and is foundational for field theory and quantum chromodynamics (QCD), the advanced theory of elementary particles. The paragraph also touches on the dissatisfaction with the standard approach to quantum mechanics and Feynman's endeavor to connect it more closely with classical mechanics, focusing on the concept of the classical trajectory and its generalization in quantum mechanics.
🔍 Exploring the Connection Between Classical Mechanics and Quantum Mechanics
The lecturer delves into Feynman's exploration of the relationship between classical mechanics and quantum mechanics, discussing the concept of the classical trajectory and its uniqueness in classical physics. The paragraph discusses the statistical nature of quantum mechanics, where multiple paths are possible, each with its own probability, contrasting with the single, unique path in classical mechanics. Feynman's approach to quantum mechanics involves considering all possible paths a particle can take, integrating over these paths to find the wave function at a point in space-time, using a function known as the propagator or Green's function. The paragraph also mentions Dirac's influence on Feynman's thought process, suggesting the consideration of Hamilton's principle, a fundamental concept in physics.
🌐 Hamilton's Principle and the Concept of Action
This paragraph focuses on Hamilton's principle, which states that the motion of a particle along the classical trajectory is such that the action is at an extremum. The action is defined as a functional of the path, involving an integral of the Lagrangian, which is the difference between the kinetic and potential energy of the particle. The lecturer explains that Hamilton's principle has been used to derive various fundamental theories in physics, including Newton's laws and Einstein's general theory of relativity. The paragraph also discusses the concept of a functional in the context of Hamilton's principle and the constraints of the system, which require that all paths begin and end at specific points in space-time.
🚀 Applying Hamilton's Principle to Quantum Mechanics
The lecturer applies Hamilton's principle to quantum mechanics, considering a free particle and its action. The action for a free particle is derived and related to the Green's function, which is a solution to the wave equation. The paragraph explains how the Green's function, or propagator, is related to the action along a path from point A to point B. It also discusses how the wave function at a point in space-time is the result of summing over all possible paths connecting that point to every other point in space, with each path weighted by its action. The paragraph concludes by highlighting the importance of Planck's constant in determining the probability of each path, with paths near the classical trajectory being the most probable due to their minimal action.
🤔 Calculating Quantum Mechanics with Path Integrals
This paragraph discusses the challenge of calculating quantum mechanics using path integrals. The lecturer explains that the Green's function for a quantum system can be expressed as a sum over all possible paths, each weighted by the exponential of the classical action divided by Planck's constant. The paragraph details the process of using a complete set of eigenstates to find the Green's function and then using this function to determine the wave function of the system. The lecturer also touches on the difficulty of the calculations involved and the need to relate the quantum mechanical Green's function to the classical action.
🔄 Wick Rotation and Imaginary Time in Quantum Mechanics
The final paragraph introduces Wick rotation, a technique used to evaluate the Green's function for imaginary values of time. This rotation transforms the oscillatory exponentials in the Green's function into decaying exponentials, simplifying the calculation. The lecturer explains that at very long imaginary times, only the ground state contributes significantly to the sum, allowing the wave function to be determined from the limit of the Green's function as imaginary time approaches infinity. The paragraph concludes by emphasizing the importance of this method in calculating quantum mechanical wave functions and the significance of the ground state in this context.
Mindmap
Keywords
💡Quantum Path Integral
💡Quantum Mechanics
💡Classical Mechanics
💡Hamilton's Principle
💡Action
💡Lagrangian
💡Green's Function
💡Wave Function
💡Field Theory
💡Quantum Chromodynamics (QCD)
💡Wick Rotation
Highlights
Introduction to Feynman's quantum path integral formulation of quantum mechanics, emphasizing its subtlety and importance.
The quantum path integral formulation provides a new perspective on quantum mechanics and is foundational for field theory and quantum chromodynamics (QCD).
Feynman's approach to quantum mechanics attempts to better connect with classical mechanics through the concept of classical trajectories.
Hamilton's principle and the concept of action are central to understanding the transition from classical to quantum mechanics in Feynman's formulation.
The classical trajectory is unique in classical mechanics, whereas quantum mechanics suggests a statistical nature involving many paths.
Feynman's vision involves considering all possible paths a particle can take, each with its own probability, in contrast to the single path in classical mechanics.
The propagator, or Green's function, is essential in Feynman's path integral formulation, representing the transition amplitude between two points in spacetime.
The connection between the quantum mechanical Green's function and the classical action is established through the least action principle.
The role of ħ (h-bar) in the path integral formulation is crucial, as it determines the probability weighting of each path.
Feynman's formulation involves a sum over all paths, each weighted by the exponential of the classical action divided by h-bar.
The classical path is favored due to its minimal action, making it the path with the highest probability in quantum mechanics.
The method to calculate the wave function from the Green's function involves Wick rotation, which simplifies the expression by considering imaginary time.
In the limit of infinite imaginary time, the contribution to the sum from all states except the ground state decays, leaving only the ground state.
The final expression for the wave function is derived from the Green's function at infinite imaginary times, providing a practical method for calculation.
The practical application of Feynman's path integral formulation in quantum field theory and QCD demonstrates its significance in modern physics.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: