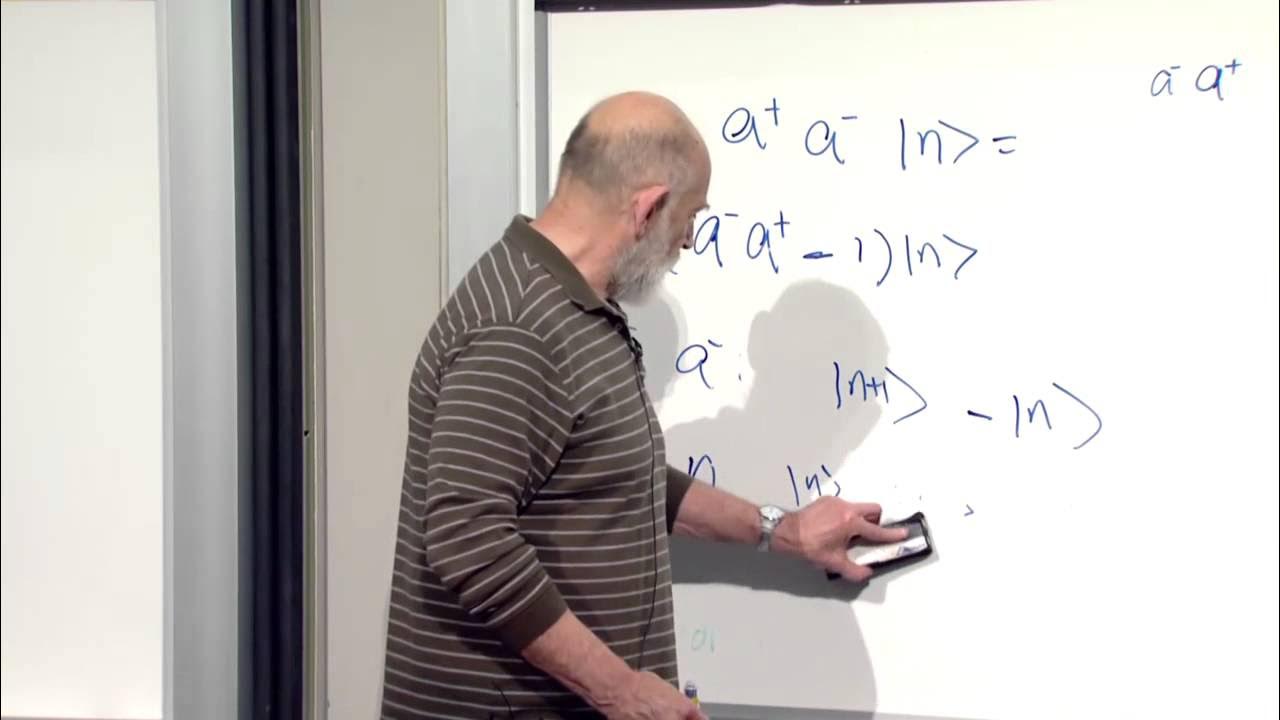Lecture 10 | New Revolutions in Particle Physics: Basic Concepts
TLDRThe video script delves into the intricacies of quantum field theory (QFT), a fundamental framework in modern physics for understanding particle interactions. It explains how QFT uses the Lagrangian to describe these interactions, and introduces the path integral method, a key technique in QFT that generalizes the principle of least action. The script explores the concept of action in classical mechanics and how it translates into the quantum realm, leading to the development of Feynman diagrams. These diagrams are a visual representation of all possible paths a particle can take, with each path's probability amplitude determined by the action along that path. The lecture also touches on the duality between particles and fields, and how the Lagrangian can be used to calculate processes involving both. It concludes with a discussion on how the Lagrangian encodes the properties of particles, such as mass, and how it can be used to predict and calculate outcomes in particle physics, despite the complexity of the underlying mathematics.
Takeaways
- 📐 **Path Integral Formulation**: Quantum field theory uses the path integral method to calculate particle interactions, which is a generalization of the principle of least action in quantum mechanics.
- ⚛️ **Quantum Fields and Particles**: The script discusses the duality between quantum fields and particles, where fields can be thought of as made up of creation and annihilation operators, representing particles.
- 🚀 **Lagrangian in QFT**: The Lagrangian is a key component in quantum field theory, describing the dynamics of fields and particles, and is used to calculate probabilities of different interactions.
- 🔢 **Action and Probability**: The action, integrated over all possible field configurations or histories, gives the probability amplitude for a particle to move from one state to another.
- 🧲 **Coupling Constants**: In particle interactions, coupling constants, which are determined by experiment, quantify the strength of the interaction at each vertex in a Feynman diagram.
- 🤹 **Complexity of Interactions**: Particle interactions can be very complex, involving the creation and annihilation of particles, and are represented by Feynman diagrams that include vertices and propagators.
- 🔴 **Conservation Laws**: The script touches on conservation laws, such as energy and momentum, which are inherent in the Lagrangian and govern what interactions can occur.
- 📈 **Small Coupling Constants**: For quantum field theory to be practical, coupling constants are often small, allowing for a convergent series in calculations.
- 🧬 **Standard Model**: The script alludes to the Standard Model of particle physics, which classifies particles and their interactions, with the Lagrangian containing terms that represent different particles and forces.
- ⚖️ **Symmetries in Physics**: Symmetries play a crucial role in particle physics, relating different coupling constants and simplifying the understanding of particle interactions.
- 🔍 **Precision of QFT**: Despite the complexity and number of parameters in the Standard Model, quantum field theory allows for precise calculations once the parameters are known.
Q & A
What is the principle of least action in classical mechanics?
-The principle of least action is a fundamental concept in classical mechanics that states the trajectory of a particle between two points in space-time is the one that minimizes the action, which is defined as the integral of the Lagrangian along the path.
How does the path integral method relate to quantum mechanics?
-The path integral method is a quantum mechanical technique that generalizes the principle of least action. It involves summing over all possible trajectories of a system to calculate the probability amplitude for a particle to move from one point to another, incorporating the action through the Lagrangian of the system.
What role does the Lagrangian play in quantum field theory?
-In quantum field theory, the Lagrangian is a function that describes the dynamics of fields, including both space and time derivatives. It is used to construct the action, which is then utilized in the path integral formulation to compute probabilities and amplitudes for various field configurations and interactions.
How does the concept of action apply to field theory?
-In field theory, the action is an integral over space and time of the Lagrangian density, which depends on the fields and their derivatives. The principle of least action is used to derive the equations of motion for the fields, and in quantum mechanics, it is used to calculate transition amplitudes between different field configurations.
What is the significance of the term 'amplitude' in quantum mechanics?
-In quantum mechanics, the amplitude is a complex number associated with a particular quantum state or process. The probability of a quantum event is determined by the square of the amplitude's magnitude. Amplitudes are crucial in calculating the likelihood of different outcomes when a quantum system is observed.
How does the concept of a particle moving in quantum field theory relate to the terms in the Lagrangian?
-The terms in the Lagrangian that involve fields at neighboring points in space-time correspond to particles moving from one location to another. These terms, often referred to as kinetic terms, allow for the calculation of the amplitude for a particle to transition between different points in the field.
What is the role of the mass term in the Lagrangian?
-The mass term in the Lagrangian, often represented as (1/2) m^2 Phi^2, where Phi is the field and m is the mass of the particle, contributes to the action by weighting paths in a way that reflects the mass of the particle. It affects the amplitude for a particle to remain in the same location without moving.
How do interaction terms in the Lagrangian give rise to particle creation and annihilation processes?
-Interaction terms in the Lagrangian, such as cubic or higher-order terms involving the field variables, can represent processes where particles are created or annihilated. For example, a cubic term can describe an interaction where one particle is annihilated and two particles are created, or vice versa.
What is the significance of the coupling constants in quantum field theory?
-Coupling constants in quantum field theory are coefficients that appear in the interaction terms of the Lagrangian. They determine the strength of the interactions between particles. If the coupling constants are small, the series of contributions to the amplitude from different interaction processes may converge, allowing for practical calculations.
How does the process of particle scattering in quantum electrodynamics (QED) relate to the fine-structure constant?
-The probability of scattering processes in QED is proportional to the square of the electric charge, which is related to the fine-structure constant (approximately 1/137). Each additional photon in a Feynman diagram involves an additional power of the electric charge, making higher-order scattering processes less probable.
What is the standard model of particle physics and how does it relate to the Lagrangian?
-The standard model of particle physics is a theoretical framework that describes three of the four known fundamental forces (excluding gravity) and the elementary particles that make up the universe. It can be formulated in terms of a Lagrangian that includes terms for each particle, their masses, and their interactions, with parameters determined by experimental data.
Outlines
😀 Introduction to Quantum Field Theory and the Lagrangian
The paragraph begins with a brief recap of quantum field theory (QFT), emphasizing the role of the Lagrangian in describing particle interactions. It outlines the path integral method, a technique in QFT that connects to Feynman diagrams. The principle of least action is introduced as a classical mechanics concept, which is then generalized for quantum mechanics and field theory. The summary explains how the action, derived from the Lagrangian, is integral to understanding the trajectory of particles and fields in space-time.
📐 The Principle of Least Action and its Quantum Mechanical Implication
This section delves into the principle of least action, highlighting its extension to space-time and its application in field theory. It discusses how the action is calculated over a region of space-time and how it leads to the equations of motion for fields. The paragraph also bridges the classical principle of least action to its quantum mechanical counterpart, emphasizing the role of action in deriving probabilities and amplitudes for particle interactions.
🚀 Amplitudes, Probabilities, and the Path Integral Formulation
The paragraph introduces the concept of amplitudes in quantum mechanics and explains how they are used to construct probabilities. It details Feynman's rule, which involves the action integrated over all possible trajectories to calculate the amplitude for a particle to move from one point to another. The paragraph also touches on the complex nature of amplitudes and how their magnitude squared represents probability, leading to the idea of probability amplitude.
🤔 The Probability Amplitude and the Sum Over Histories
This section explores the idea of probability amplitude in the context of a field starting in an arbitrary configuration and evolving over time. It discusses the sum over all possible field configurations, or 'histories,' and how this relates to the path integral formulation. The paragraph questions the convergence of these integrals and explains that despite the complexity, these integrals do converge under certain conditions.
🔄 The Discrete Formulation of Path Integrals and Particle Representation
The paragraph presents a discrete approach to path integrals by dividing space-time into cells and considering field values in each cell. It discusses how this method allows for the calculation of probability amplitudes in a more tangible way. The concept of initial and final conditions in this discrete space-time is also explained, along with the idea of summing over all possible field configurations between these conditions.
🧲 Particle Interactions and the Role of the Lagrangian
This section focuses on how the Lagrangian is used to calculate processes involving particles moving and interacting. It touches on the duality between particle and field descriptions in quantum field theory and how one might calculate the probability of transitioning from one particle state to another. The paragraph also discusses the concept of dividing space-time into cells and the role of the Lagrangian in each cell.
🎓 Quantum Field Theory and the Complexity of Interactions
The paragraph discusses the complexity of interactions in quantum field theory, where particles can split and join, leading to a multitude of possible paths from an initial to a final state. It explains that the Lagrangian governs these interactions and that the amplitude for each path can be found by expanding the action and identifying the relevant terms. The paragraph also emphasizes the importance of conservation laws and the role of coupling constants in determining the convergence of the sum of amplitudes.
🧬 The Standard Model of Particle Physics and its Components
This section outlines the components of the standard model of particle physics, including a list of particles, their masses, and coupling constants. It highlights the role of the Lagrangian in describing these particles and their interactions. The paragraph also discusses the importance of symmetries in understanding relationships between different particles and processes, and how these symmetries can sometimes relate different coupling constants.
🤓 Quantum Electrodynamics and the Fine Structure Constant
The final paragraph focuses on quantum electrodynamics (QED), a subset of quantum field theory that involves the interaction of electrons and photons. It discusses how the electric charge, or coupling constant, plays a crucial role in determining the probability of different scattering processes. The paragraph explains the concept of the fine-structure constant and how it relates to the likelihood of photon scattering by an electron.
Mindmap
Keywords
💡Quantum Field Theory
💡Lagrangian
💡Path Integral Method
💡Feynman Diagrams
💡Principle of Least Action
💡Action
💡Space-Time
💡Probability Amplitude
💡Particle Interactions
💡Field Quanta
💡Derivative Terms
Highlights
Quantum field theory is introduced as a method for understanding particle interactions through the Lagrangian.
The path integral method is described as the most direct route to the theory of particle interactions based on Feynman diagrams.
The principle of least action is generalized for quantum mechanics and quantum field theory, relating to the action along a trajectory or field history.
The action in quantum field theory is an integral over space and time, contrasting with the particle trajectory integral over time alone.
The concept of a field history is explained as a trajectory in field space, specifying field values along an initial surface.
Feynman's rule is presented for calculating amplitudes in quantum mechanics, involving the sum over all possible classical routes.
The amplitude for a particle to move from one point to another in quantum mechanics is derived from the action integral over all trajectories.
The transition from quantum mechanics to classical theory is discussed in terms of stationary action and least cancellation of amplitudes.
The Lagrangian is used to calculate processes involving particles moving and interacting, emphasizing the duality between fields and particles.
Lattice gauge theory is mentioned as a tool for practical computation in quantum field theory, involving summing over all possible field configurations on a discrete space.
The importance of the derivative terms in the Lagrangian for representing particle motion is highlighted.
The mass term in the Lagrangian is associated with the probability amplitude for a particle to remain in the same place.
Interaction terms in the Lagrangian, such as cubic terms, allow for processes where particles are created and annihilated in different numbers.
The concept of coupling constants in the Lagrangian is introduced, which influence the complexity and probability of particle interactions.
Feynman diagrams are used to visualize and calculate the amplitudes for various particle interactions, including the emission and absorption of photons.
The fine-structure constant is discussed in the context of quantum electrodynamics, determining the probability of photon scattering by an electron.
The standard model of particle physics is referenced as a culmination of the discussed theories, incorporating a list of particles, their masses, and symmetries.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: