17.8 Feynman Quantum Path Integrals II
TLDRThis script delves into the fascinating world of quantum mechanics through the lens of Feynman's path integral formulation. It explains the transition from continuous space-time to a discrete lattice, simplifying complex equations into an algorithmic approach. The lecture explores the use of Euler's method, the concept of Wick rotation, and the application of Monte Carlo simulations to approximate quantum behavior. It also encourages practical engagement with the material through coding exercises, aiming to bridge the gap between theoretical quantum mechanics and its computational simulation.
Takeaways
- 🧩 The script introduces the concept of lattice quantum mechanics, which involves discretizing space and time into intervals to simplify solving equations for quantum systems.
- 🔍 It explains that in lattice quantum mechanics, calculations are performed only at discrete points on a 'lattice' rather than for all continuous values of space and time.
- 📐 The script discusses the use of paths and links in the algorithm, replacing the concept of smooth paths with a series of straight line segments, each with a uniform time step.
- 🔄 The algorithm uses Euler's method for simplicity, despite its known inaccuracies, to calculate the derivative with respect to time.
- ⚖️ The action for each link is calculated using the Lagrangian, which is assumed to be constant over each link, and is related to the kinetic and potential energy.
- 🌐 The script describes the process of calculating the Green's function through a sum over all paths from point A to point B, involving exponential terms based on the action.
- 🔮 Wick rotation is introduced as a method to transform the Lagrangian into the Hamiltonian by evaluating it at a negative imaginary time, simplifying quantum mechanics calculations.
- 🔄 The script explains that the Schrödinger equation can be transformed into a heat diffusion equation through Wick rotation, allowing for the use of Monte Carlo techniques to solve it.
- 📊 The algorithm involves the Metropolis algorithm to test all possible paths and let the system equilibrate, which is similar to methods used in statistical mechanics.
- 📉 The script suggests that the accuracy of the algorithm can be improved by decreasing the time step (delta t) and space step (delta x), leading to a smoother wave function.
- 🔮 The script encourages exploring the effects of changing Planck's constant (h-bar) to understand its impact on quantum mechanics, with larger values leading to more pronounced quantum effects.
Q & A
What is the main topic discussed in the script?
-The script discusses the concept of lattice quantum mechanics and its application in algorithmic computation, particularly focusing on the path integral formulation of quantum mechanics and its relation to statistical fluctuations.
What is lattice quantum mechanics?
-Lattice quantum mechanics is a method where space and time are imagined as being broken up into discrete intervals or 'lattices'. Instead of solving equations for all possible space and time values, the equations are solved for points on the lattice only.
What is the significance of Euler's rule in the context of this script?
-Euler's rule is used in the script to simplify the calculation process. It approximates the derivative with respect to time as the difference in space value divided by the uniform time step epsilon, despite its known high error rate, due to its simplicity.
What is the role of the Greens function in the algorithm?
-The Greens function is crucial in the algorithm as it involves a sum over all possible paths from point A to point B. It helps in evaluating the wave function and understanding how particles propagate through space and time in quantum mechanics.
What is the Wick rotation mentioned in the script, and what does it achieve?
-The Wick rotation is a method where real time is transformed into imaginary time. It simplifies calculations by rotating the Lagrangian into the Hamiltonian and the Schrödinger equation into the heat diffusion equation, making quantum mechanical problems more tractable.
How does the script relate quantum mechanics to heat diffusion equations?
-The script shows that by applying the Wick rotation, the Schrödinger equation can be transformed into a heat diffusion equation. This connection allows for the use of Monte Carlo techniques, which are familiar for solving heat equations, to be applied in quantum mechanical computations.
What is the purpose of the Monte Carlo simulations in the context of the script?
-Monte Carlo simulations are used to solve the heat diffusion equation that results from the Wick rotation. They help in evaluating the path integrals by simulating the statistical fluctuations of paths in quantum mechanics.
How does the script describe the process of equilibration in quantum mechanics?
-The script describes equilibration as a process where the system is allowed to run for a long time, not necessarily infinite, to stabilize at a point where the Greens function equilibrates to the ground state. This is similar to the concept of equilibration in the Ising model.
What is the significance of the Boltzmann factor in the script?
-The Boltzmann factor is used to weight each path in the path integral by a factor that is related to the energy of the path and the time step. It is crucial for the Monte Carlo simulations, as it represents the probability of a path occurring in the system.
How should one test the algorithm discussed in the script?
-The algorithm should be tested by plotting the classical trajectory and the actual space-time paths generated by the algorithm. Additionally, one should vary parameters such as delta x and delta t to observe the effects on the precision and accuracy of the computed wave function.
Outlines
🧠 Introduction to Lattice Quantum Mechanics and Algorithms
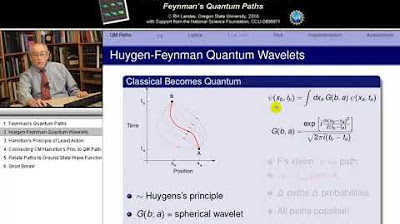
The speaker introduces the concept of lattice quantum mechanics, explaining how space and time are discretized into intervals to form a lattice. This approach simplifies the process of solving equations by focusing only on lattice points rather than continuous values. The algorithm discussed is based on this discretization, and the use of Euler's rule for simplicity, despite its inaccuracies. The explanation transitions into discussing the action for each link in the lattice and how it contributes to the total action for a path, which is essential for calculating the Green's function.
🔄 Wick Rotation and Path Integral Formulation
The discussion continues with the application of Wick rotation, which transforms real time into imaginary time, and the Lagrangian into the Hamiltonian. This rotation simplifies quantum mechanics by allowing the use of path integrals, where the action is evaluated over discrete paths rather than continuous space-time. The speaker explains how the Lagrangian, when evaluated at negative imaginary time, corresponds to the Hamiltonian at ordinary time, and how this relates to the path integral formulation of quantum mechanics.
🔗 Quantum Mechanics and Classical Trajectories
The speaker delves into the relationship between quantum mechanics and classical trajectories, emphasizing that quantum particles can be thought of as traveling along classical paths with fluctuations. This perspective is based on Hamilton's principle of least action, where the action is minimal along the classical path and varies quantum mechanically in the vicinity of this path. The concept of a path integral is introduced as the sum of all possible trajectories in space-time, each weighted by a quantum mechanical factor.
📊 Algorithmic Computation of Quantum Mechanics
The focus shifts to the practical computation of quantum mechanics using an algorithmic approach. The speaker describes an applet and Python code that simulate the process of computing quantum mechanics, demonstrating how different trajectories are tried out in real-time and how a wave function builds up over time. The algorithm involves summing over links in a path integral and integrating over all possible x values, which is akin to solving for equilibrium in the Ising model.
🔄 Exploring Quantum Fluctuations and Algorithm Testing
The speaker discusses the process of exploring quantum fluctuations by flipping links in the path and observing how new paths with the same energy can be generated. The algorithm uses the Metropolis algorithm to try out all possible paths in space, allowing the system to equilibrate and stabilize. The speaker encourages testing the algorithm by changing the values of delta x and delta t to achieve better precision and accuracy in the computed wave function.
📚 Analytical Testing and Quantum Effects
The speaker suggests analytical testing of the algorithm by comparing computed results with known solutions, such as those for the harmonic oscillator and the quantum bouncer. The importance of h-bar in quantum mechanics is highlighted, with the speaker advising to experiment with different values of h-bar to observe the effects on quantum behavior and its deviation from classical trajectories.
🚀 Conclusion and Encouragement for Further Exploration
In conclusion, the speaker summarizes the alternative view of quantum mechanics presented by Feynman, which involves particles traveling along classical trajectories with quantum fluctuations. The speaker encourages further exploration and calculations to understand and validate this perspective, acknowledging its complexity but also its potential as a correct vehicle for understanding quantum mechanics. The potential application of this approach in field theory calculations, such as quantum chromodynamics, is also mentioned.
Mindmap
Keywords
💡Lattice Quantum Mechanics
💡Path Integral
💡Lagrangian
💡Hamiltonian
💡Euler's Rule
💡Metropolis Algorithm
💡Green's Function
💡Wave Function
💡Wick Rotation
💡Quantum Monte Carlo
💡Harmonic Oscillator
Highlights
Introduction to lattice quantum mechanics, a discrete space-time model for algorithmic computation.
Transition from theory to algorithm, simplifying complex equations to a more manageable form.
Explanation of lattice points as the basis for solving quantum mechanics problems algorithmically.
Use of Euler's rule for its simplicity in approximating derivatives in the algorithm.
Derivation of the action for a single link in the lattice model.
Expression of the action in terms of kinetic energy and potential energy within the algorithm.
Calculation of the total action for a path by summing over all links.
Introduction of the Greens function and its significance in evaluating the algorithm.
Wick rotation's role in transforming the Lagrangian into the Hamiltonian within the quantum mechanics framework.
Connection between the imaginary time Lagrangian and the real Hamiltonian.
Algorithmic computation of the wave function using Feynman's path integral formulation.
The equivalence of solving the Schrödinger equation at imaginary time to solving a heat diffusion equation at real time.
Application of Monte Carlo techniques to solve heat equations in quantum mechanics.
Importance of high temperature limits in achieving accurate computational results.
Demonstration of quantum fluctuations and the building up of the wave function through an applet.
Use of the Metropolis algorithm in the Quantum Monte Carlo method for path evaluation.
Testing the algorithm with different values of h-bar to observe quantum effects.
Summary of the path integral formulation as an alternative view of quantum mechanics.
Challenges and future prospects of applying the path integral approach beyond the ground state.
Invitation to explore Quantum Chromodynamics calculations using the path integral method.
Final summary emphasizing the satisfaction and correctness of the path integral approach in quantum mechanics.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: