Lecture 7 | String Theory and M-Theory
TLDRThe video script delves into the intricacies of string theory and quantum mechanics, focusing on the concept of path integrals. It explains how in classical mechanics, the trajectory of a particle is determined by the principle of least action, which is also a fundamental principle in quantum mechanics but with a different application. Instead of finding a single trajectory, quantum mechanics involves integrating over all possible trajectories to calculate the amplitude of a particle transitioning from one state to another. This is achieved through the use of complex analysis and the clever trick of transforming the time variable, often denoted as 'tau' to 'i tau', which simplifies the path integral formulation. The script further explores the application of these principles to string theory, where particles are replaced by one-dimensional objects—strings—and the path integral is performed over all possible two-dimensional surfaces, or 'world sheets', that the strings can trace out. The video also touches on the mathematical beauty of the subject, including the role of conformal mappings in simplifying the equations of motion for strings and the concept of channel duality, which is a symmetry between different ways of visualizing particle interactions. Overall, the script provides a rich exploration of the mathematical foundations of quantum mechanics and string theory, offering viewers a deeper understanding of these complex and fascinating areas of physics.
Takeaways
- 📐 **Space-Time View in String Theory**: The lecture introduces a space-time perspective on string theory, emphasizing the mathematical framework that underpins it.
- ⏱️ **Classical vs. Relativistic Trajectories**: It contrasts the description of a particle's trajectory in classical mechanics with that in relativistic physics, highlighting the use of proper time.
- 🔑 **Principle of Least Action**: The principle of least action is a fundamental concept used to define the motion of particles in classical physics, which is extended into quantum mechanics.
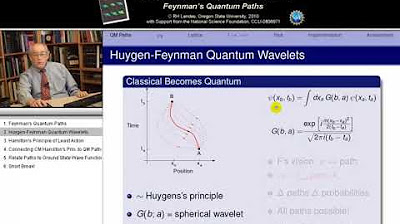
- 🚀 **Quantum Mechanics and Path Integrals**: The script explains how in quantum mechanics, the action is used to calculate the amplitude of a particle transitioning between two points by summing over all possible trajectories.
- 🎭 **The Role of the Action in Quantum Field Theory**: In quantum field theory, the action is integrated over all trajectories to calculate the amplitude for particle interactions, which is visualized through Feynman diagrams.
- 🧮 **Complexity of Path Integrals**: The script acknowledges the mathematical complexity and challenges of path integrals, which involve infinite-dimensional integrals and are not well-defined in a traditional sense.
- 🔄 **Conformal Mapping in String Theory**: The importance of conformal mappings in string theory is discussed, which allow for the transformation of the problem into a more symmetric and manageable form.
- 🔗 **Duality Between S-Channel and T-Channel**: The concept of channel duality is introduced, showing how one structure can describe both particle formation and decay (S-channel) and particle exchange (T-channel).
- 🧲 **Conformal Invariance**: The script touches on the significance of conformal invariance in the action of the string, which allows for the application of different coordinate systems without changing the physics.
- 🌀 **World Sheet Topology**: It is explained that the world sheet, which represents the history of a string, can be thought of as a surface that varies in complexity, from a simple ribbon to a surface with holes.
- ⚙️ **Analytic Continuation**: The trick of analytic continuation is used to make the path integrals more manageable by rotating the time variable into the complex plane, which is a common technique in quantum field theory.
Q & A
What is the main concept of string theory discussed in the transcript?
-The main concept discussed is the space-time view of string theory, particularly focusing on the path integral formulation where particles are described as strings with world sheets, and the action for a string is defined on these two-dimensional surfaces.
How does the principle of least action apply in both classical and quantum mechanics?
-In classical mechanics, the principle of least action is used to find the trajectory of a particle by minimizing the action subject to certain constraints. In quantum mechanics, the action is used to find the amplitude of a particle transitioning from one state to another by summing over all possible trajectories, which is known as the path integral formulation.
What is the significance of the variable 'alpha' in the trick used to deal with path integrals?
-The variable 'alpha' is introduced as a scaling factor in a change of variables trick to make the path integral more manageable. By choosing 'alpha' to be imaginary (-i), the exponent in the path integral becomes real, which helps in suppressing contributions from wild trajectories and focusing on the physically relevant ones.
How does the action for a string differ from that of a point particle?
-The action for a point particle is an integral over time of its kinetic energy. For a string, the action is an integral over the two-dimensional world sheet and includes terms involving both temporal and spatial derivatives, reflecting the string's extended nature and its motion through space-time.
What role does the parameter 'tau' play in the description of a particle's trajectory?
-'Tau' is a parameter that denotes proper time along the trajectory of a particle. In the context of the transcript, it is used in both nonrelativistic and relativistic physics to describe the trajectory of a particle as a function of this parameter.
What is the mathematical challenge associated with path integrals in quantum mechanics?
-The mathematical challenge with path integrals is that they involve an infinite-dimensional integral over all possible trajectories of a particle. This integral is not well-defined in a traditional sense and requires sophisticated techniques, such as analytic continuation, to make it convergent and physically meaningful.
How does the concept of conformal mappings relate to the string path integral?
-Conformal mappings are transformations that preserve angles and locally preserve shape. They are crucial in string theory because they allow the path integral to be formulated in different coordinate systems, such as mapping from a complex plane to a unit disk, without changing the physical content described by the Laplace equation for the string's dynamics.
What is the physical interpretation of the 'S' and 'T' channels in the context of scattering amplitudes?
-The 'S' channel refers to the process where two particles come together to form an intermediate state, while the 'T' channel describes the exchange of a particle between two other particles. These channels are related by duality, and their symmetry is a manifestation of the underlying conformal invariance of the string path integral.
Why is the amplitude for a string transitioning between two configurations important in quantum mechanics?
-The amplitude for a string transitioning between configurations is important because it provides the probability of finding the string in a certain state at a later time, given its initial state. This is a fundamental aspect of quantum mechanics, where the path integral formulation gives a way to calculate these probabilities.
What is the significance of the Laplace equation in the context of the string path integral?
-The Laplace equation is significant because it is the equation of motion derived from the action for the string. It describes the classical behavior of the string in the absence of quantum fluctuations. When quantum mechanics is considered, the path integral formulation involves integrating over all configurations that satisfy the Laplace equation.
How does the concept of duality arise in the string path integral?
-Duality arises because the same mathematical structure can describe both the formation and decay of particles (S channel) and the exchange of particles (T channel). This duality is a consequence of the conformal invariance of the string path integral, which allows for different interpretations of the same mathematical expressions.
Outlines
📐 Classical and Relativistic Trajectories in Particle Physics
The first paragraph introduces the concept of describing an ordinary particle's trajectory within classical and relativistic physics. It explains the use of three-dimensional position 'X' as a function of time 'T' in classical mechanics and the four-dimensional position with space and time components 'X mu' as a function of proper time 'tau' in relativistic physics. The principle of least action is used to define the motion of a particle, with the action 'S' being the integral over time of the kinetic energy for a non-relativistic particle. The paragraph also touches on the transition to quantum mechanics, where the focus shifts from finding a trajectory to calculating the amplitude for a particle to move from one point to another, using the action within an exponential function.
🚀 Quantum Mechanics and Path Integrals
The second paragraph delves into quantum mechanics, contrasting it with classical mechanics by focusing on the amplitude of a particle's movement rather than its trajectory. It discusses the concept of path integrals, where the amplitude is calculated by integrating over all possible trajectories, which is a complex, infinite-dimensional integral. The paragraph also introduces the idea of a propagator in relativistic physics, which calculates the amplitude for a particle to move from one point to another and can be used to consider more complex processes involving particle interactions. A trick used by physicists to deal with these complex integrals is also mentioned, which involves focusing on the classical trajectories that correspond to the straight-line motion, as these are deemed most important.
🧮 The Trick of Path Integrals and Justification
The third paragraph explains a trick used in physics to deal with the complex integrals encountered in path integrals. This trick involves changing the integration variable 'tau' to a new variable 's', which is a multiple of 'tau'. The choice of the multiplier 'alpha' is left arbitrary and is intended to be chosen later for convenience. The paragraph discusses the mathematical manipulation involved in this change of variables and the implications it has for the action within the integral. The trick is said to always work and provide the correct answer once justified, despite being as challenging to understand as the original integral.
🔍 The Wiener Integral and Analytic Continuation
The fourth paragraph continues the discussion on path integrals, focusing on the Wiener integral, a form of path integral used in statistical mechanics. It explains how by choosing a specific value for 'alpha', the integral can be made more manageable by suppressing contributions from trajectories that deviate significantly from the classical path. The paragraph also touches on the process of analytic continuation, a method used by physicists to deal with the complexities of path integrals by evaluating them at complex points. This technique allows for the calculation of path integrals by turning the time variable on its side and then extrapolating the results to the desired complex values.
🎼 String Theory and Path Integrals
The fifth paragraph introduces string theory, where particles are not points but one-dimensional objects—strings. It discusses the action of a string, which is described by its position 'X' as a function of two variables, 'tau' and 'sigma', parameters of the string's worldsheet. The action is defined as an integral over the worldsheet, involving derivatives of 'X' with respect to 'tau' and 'sigma'. The paragraph explains that the string's path integral involves integrating over all possible worldsheet configurations, which is a complex task due to the infinite variability of the surfaces. The paragraph concludes by noting that the action for a string can be generalized to include interactions, such as two strings joining or splitting.
🧵 Generalizing String Interactions
The sixth paragraph explores the generalization of string interactions beyond a single string to multiple strings. It discusses how the path integral approach can be used to calculate the amplitude for strings to interact, such as two strings joining to form a third or splitting into multiple strings. The paragraph emphasizes the complexity of these calculations due to the infinite variety of possible worldsheet surfaces. It also mentions the possibility of including surfaces with holes in the path integral, which corresponds to summing over all Feynman diagrams with various topologies and loop numbers in quantum field theory.
🔗 Conformal Invariance in String Theory
The seventh paragraph discusses the concept of conformal invariance in the context of string theory. It explains that the action for a string, which is invariant under certain transformations of the worldsheet coordinates, allows for a variety of coordinate systems that will all yield the same physical results. The paragraph also introduces the idea of the Laplace equation in two dimensions, which is derived from the string's action and is invariant under conformal transformations. These transformations preserve angles and can map the worldsheet onto different shapes while maintaining the form of the Laplace equation.
🔄 Conformal Mappings and Duality
The eighth paragraph delves deeper into conformal mappings, explaining how they can be used to transform the worldsheet into different shapes without altering the underlying physics described by the Laplace equation. It discusses the properties of conformal mappings, such as preserving angles and shapes for small enough regions. The paragraph also touches on the application of conformal mappings in areas like cartography, where they are used to preserve the shape of small features on a map. It concludes by mentioning the use of conformal mappings in string theory to describe the splitting and joining of strings, highlighting the one-parameter family of such transformations.
🔄 Channel Duality and S-Matrix
The ninth paragraph explains the concept of channel duality in the context of scattering amplitudes in string theory. It discusses how the integral over the time interval between the joining and splitting of strings can be translated into a one-parameter integral over the positions of the points on the worldsheet. The paragraph highlights the symmetry between the S-channel and T-channel descriptions of particle interactions, which is a consequence of conformal symmetry. It concludes by noting that this duality was initially considered a remarkable feature of string theory, as it showed that one integral could account for both the formation and decay of particles as well as the exchange of particles between them.
🔄 The Miracle of Duality and S-Matrix Interpretation
The final paragraph reflects on the initial perception of channel duality in string theory as a miraculous symmetry between the S-channel and T-channel. It discusses how this symmetry was later understood to arise from conformal symmetry, which allows for a more symmetric representation of the interactions. The paragraph also touches on the role of the coupling constant in these interactions and how it enters as a multiplicative factor in the integrals. It concludes with a prompt for further information, directing interested individuals to Stanford's website.
Mindmap
Keywords
💡String Theory
💡Space-Time
💡Action (Physics)
💡Proper Time
💡Path Integral
💡Quantum Mechanics
💡Relativistic Physics
💡Worldsheet
💡Conformal Mapping
💡Mandelstam Variables
💡Duality
Highlights
Introduction to the space-time view of string theory and its comparison with classical mechanics.
Explanation of how an ordinary particle's trajectory can be described in both nonrelativistic and relativistic physics.
Discussion on the principle of least action in defining the motion of a particle.
Transition to quantum mechanics and the concept of amplitude for a particle to move from one point to another.
Introduction of the path integral, a quantum mechanical version of the principle of least action.
The challenge of infinite-dimensional integrals in quantum mechanics and the use of the trick involving the change of variables.
Explaining the trick of turning a time variable on its side to make path integrals more manageable.
Moving on to string theory, describing a particle not as a point but as a string with a world sheet.
The action for a string and its generalization to account for the two-dimensional world sheet.
The concept of integrating over all possible surfaces to find the amplitude for a string to transition between configurations.
Addressing the issue of non-convergence of the path integral for strings and the application of analytical continuation.
The relationship between string theory and the sum over all Feynman diagrams, including those with different topologies and loops.
Invariance of the Lagrangian under certain transformations of the Sigma-Tau plane.
Conformal mappings and their significance in preserving the form of the Laplace equation.
The use of analytic continuation (Wiener integral) in statistical mechanics and its relevance to string theory.
Discussion on the Nambu-Goto action and its role in string theory.
The Polyakov action and its relation to string theory, providing an alternative form of the action.
Exploration of the mathematical structure of the Laplace equation in the context of string theory.
The concept of duality between the S-channel and T-channel in particle interactions as revealed through string theory.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: