AP Physics B 2013 Question 6 - Electromagnetism

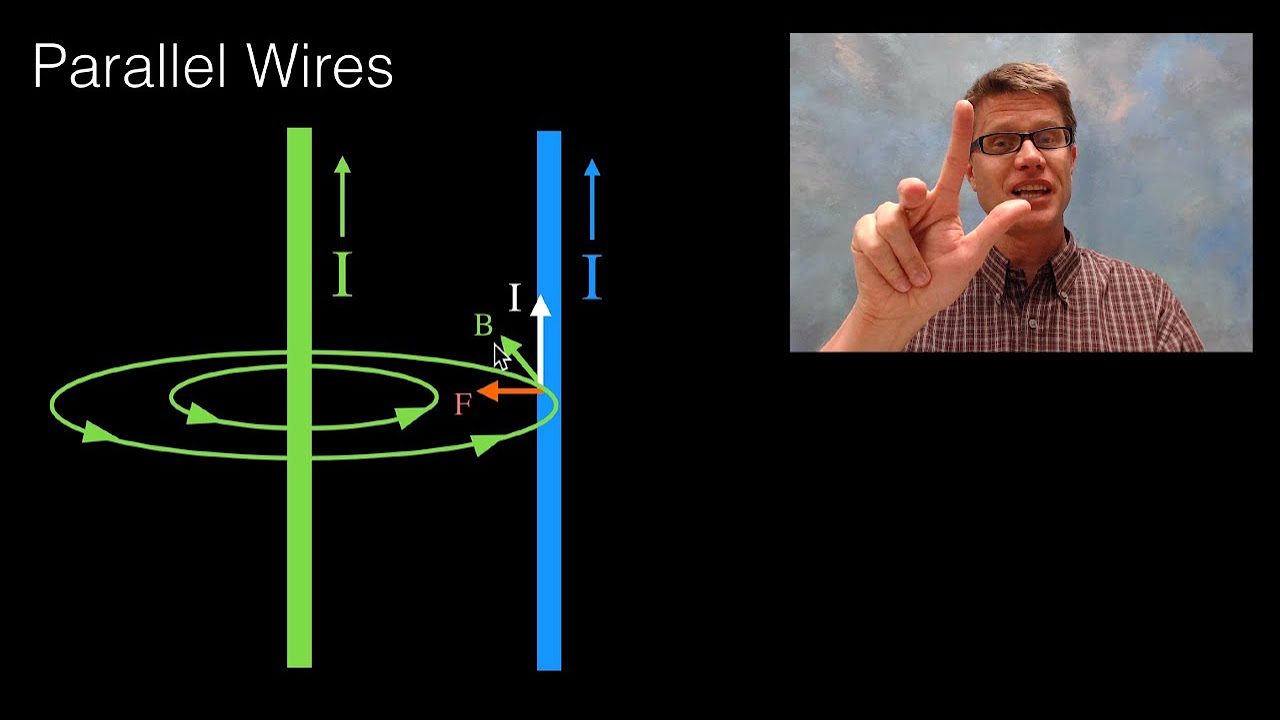
This paragraph discusses the calculation of the magnetic field produced by a wire (Wire X) at a point 0.025 meters away from it. The current flowing through Wire X is 65 amps. The formula used for the magnetic field (B) is B = μ₀I / 2πr, where μ₀ (the permeability of free space) is 4π x 10⁻⁷ Tm/A, I is the current (65 A), and r is the distance (0.025 m). Substituting these values, the magnetic field at the specified location is calculated to be 5.2 x 10⁻⁴ Tesla.

This paragraph explains how to determine the current in Wire Y, which is suspended at rest below Wire X due to the magnetic force between the wires. The magnetic force must balance the weight of Wire Y for equilibrium. The formula used is F = BIL, where B is the magnetic field (5.2 x 10⁻⁴ T), I is the current, and L is the length of Wire Y. Given the mass per unit length (5.6 x 10⁻³ kg/m) and acceleration due to gravity (10 m/s²), the current in Wire Y is calculated using I = (mass per unit length x g) / (B x L), resulting in approximately 108 amps. The direction of the current in Wire Y is determined to be the same as that in Wire X, making the wires attractive and keeping Wire Y suspended.

This paragraph describes the initial motion of Wire Y when it is moved closer to Wire X. Since the magnetic force between the wires depends inversely on the distance, moving Wire Y closer increases the force, making it greater than the weight of Wire Y. This results in a net force toward Wire X, causing Wire Y to accelerate toward Wire X.

This paragraph discusses the changes needed to maintain equilibrium if Wire Y is moved above Wire X. Previously, the attractive force between the parallel currents in the same direction kept Wire Y suspended. Now, to maintain equilibrium with Wire Y above, the currents in the wires must be antiparallel to repel each other. This would provide an upward magnetic force to balance the downward gravitational force.

This paragraph focuses on the induced EMF in Wire Y when it is moved upward at a constant speed after being disconnected from its circuit. The wire, now 1.2 meters long and moving at 3 m/s, experiences a changing magnetic flux, inducing an EMF. Using the formula EMF = B L v, where B is the magnetic field (2.6 x 10⁻⁴ T, recalculated for the new distance), L is the length of the wire, and v is the velocity, the induced EMF is calculated to be 9.4 x 10⁻⁴ volts.

This paragraph discusses identifying the higher electric potential end of Wire Y, considering the induced EMF. Using the right-hand rule for a moving conductor in a magnetic field, the direction of the induced current and thus the potential difference across the wire is determined. The wire moves up through a magnetic field pointing out of the page, leading to a force on the electrons to the right. Consequently, the right end of the wire becomes positive, and the left end negative.