Magnetism, Magnetic Field Force, Right Hand Rule, Ampere's Law, Torque, Solenoid, Physics Problems
TLDRThis video script offers an in-depth exploration of magnetism, focusing on the principles of magnetic fields, their creation by moving electric charges, and the resulting forces on wires and charged particles. It explains how bar magnets interact, with like poles repelling and opposite poles attracting, and delves into the concept of magnetic fields around a current-carrying wire, using the right-hand rule to determine field direction. The script presents the formula for calculating magnetic field strength and its dependency on current and distance from the wire. It also addresses the calculation of magnetic force on a current-carrying wire within a magnetic field, highlighting factors like current, magnetic field strength, wire length, and the angle between them. The video further discusses the magnetic force on a single moving charge, such as a proton or electron, and how to determine the radius of curvature for a charged particle moving in a magnetic field. The principles of Ampere's Law are also covered, including its application in calculating the magnetic field of a solenoid and the torque on a current-carrying loop in a magnetic field. The script concludes with problems to apply these concepts, fostering a comprehensive understanding of magnetism and its applications.
Takeaways
- 🧲 Understanding Magnetism: Like magnetic poles repel each other, while opposite poles attract due to the magnetic field lines being in the same direction.
- 🌀 Magnetic Field Creation: Magnetic fields are generated by moving electric charges, such as the flow of electric current through a wire, which creates a circular magnetic field around it.
- ✋ Right Hand Rule: To determine the direction of the magnetic field around a current-carrying wire, use the right hand rule by pointing the thumb in the direction of the current and curling the fingers, which indicates the direction of the magnetic field lines.
- 📐 Calculating Magnetic Field Strength: The strength of the magnetic field around a wire is calculated using the formula B = μ₀ * I / (2 * π * r), where B is the magnetic field strength, μ₀ is the permeability of free space, I is the current, and r is the distance from the wire.
- 🔋 Magnetic Force on a Wire: The force exerted on a current-carrying wire in a magnetic field is given by F = I * L * B * sin(θ), where F is the force, I is the current, L is the length of the wire in the magnetic field, B is the magnetic field strength, and θ is the angle between the current and the magnetic field.
- 💥 Force Direction: The direction of the magnetic force on a moving charge is perpendicular to both the direction of the charge's motion and the magnetic field, as determined by the right hand rule.
- ⚖️ Torque on a Magnetic Loop: A current-carrying loop in a magnetic field experiences a torque that causes it to rotate, with the maximum torque occurring when the magnetic field is perpendicular to the plane of the loop.
- 🔁 Solenoid Magnetic Field: The magnetic field at the center of a solenoid is given by B = μ₀ * n * I, where n is the number of turns per unit length, and is directly proportional to the current and the number of turns, and inversely proportional to the length.
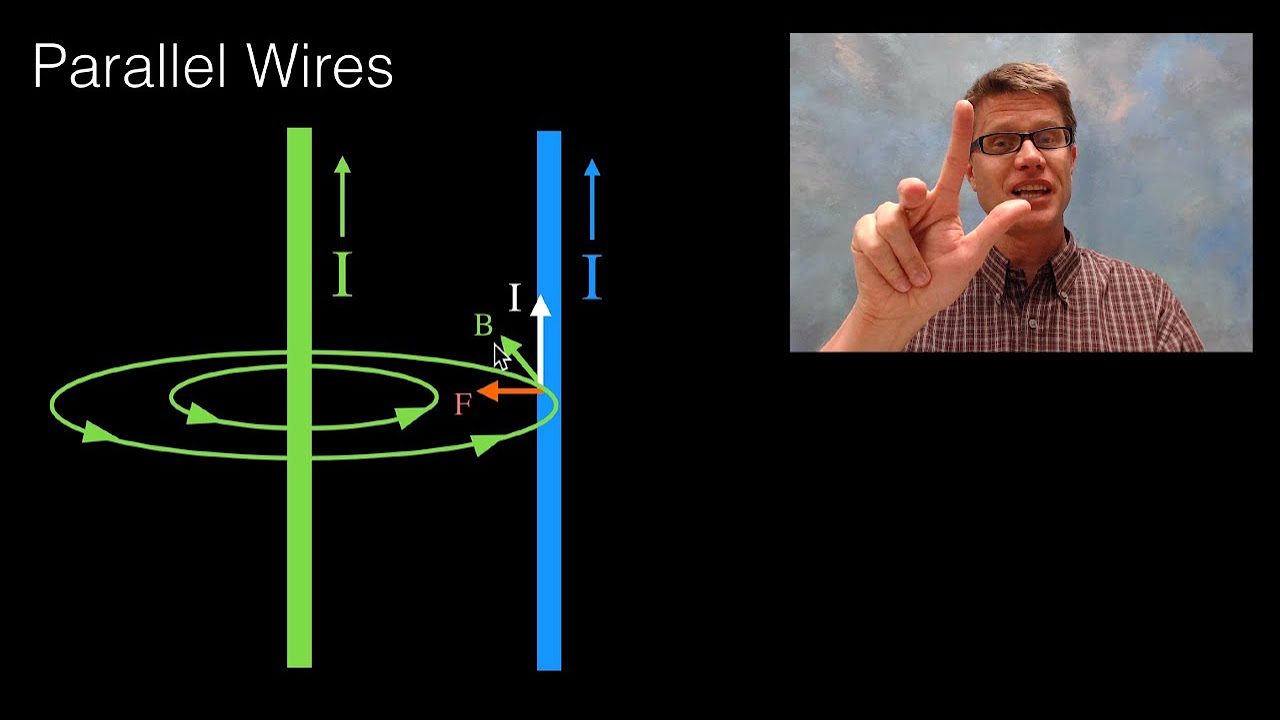
- 🤝 Attraction and Repulsion in Wires: Parallel wires carrying current in the same direction attract each other due to the magnetic field created by one influencing the other.
- 💫 Electron Volt (eV): Energy in the context of small particles like protons and electrons is often measured in electron volts, where 1 eV equals 1.6 × 10^(-19) joules, representing the energy gained by an electron when it passes through an electric potential difference of one volt.
- 🔵 Magnetic Dipole Moment: The product n * I * A, where n is the number of loops, I is the current, and A is the area of the loop, represents the magnetic dipole moment (M), which is a measure of the magnetic strength and orientation of the magnetic dipole.
Q & A
What happens when the north pole of one bar magnet is placed near the north pole of another?
-When the north pole of one bar magnet is placed near the north pole of another, the two magnets repel each other due to like magnetic poles repelling.
How is a magnetic field created around a wire?
-A magnetic field around a wire is created when electric current flows through the wire. This magnetic field is circular and its direction depends on the direction of the current, which can be determined using the right-hand rule.
What is the right-hand rule used for in electromagnetism?
-The right-hand rule is used to determine the direction of the magnetic field around a current-carrying wire. By curling the fingers around the wire with the thumb pointing in the direction of the current, the direction your fingers point represents the magnetic field lines.
How does the distance from a wire affect the strength of the magnetic field?
-The strength of the magnetic field decreases as the distance from the wire increases. This is because the magnetic field strength is inversely proportional to the distance from the wire, as described by the formula B = (μ₀I)/(2πr).
What role does the permeability of free space (mu-zero) play in calculating magnetic fields?
-The permeability of free space (μ₀) is a constant used in calculating the magnetic field produced by an electric current. It appears in formulas that describe the magnetic field in terms of current intensity and distance, indicating how the vacuum of space responds to magnetic fields.
Explain how the magnetic force on a wire in a magnetic field is calculated.
-The magnetic force on a wire in a magnetic field can be calculated using the formula F = I × L × B × sin(θ), where I is the current, L is the length of the wire within the magnetic field, B is the magnetic field strength, and θ is the angle between the wire and the magnetic field direction.
Describe what happens when two parallel wires carry currents in the same direction.
-When two parallel wires carry currents in the same direction, they attract each other. This attraction is due to the magnetic fields created by each wire, which interact in a way that pulls the wires together.
How does the angle between the current direction and magnetic field affect the magnetic force experienced by a wire?
-The angle between the current direction and the magnetic field affects the magnetic force in that the force is maximal when the angle is 90 degrees (perpendicular). The force decreases as the angle approaches zero degrees, where it becomes zero when the current is parallel or anti-parallel to the magnetic field.
What is the significance of the 'number of turns per meter' in a solenoid?
-The 'number of turns per meter' in a solenoid is significant because it indicates the density of wire loops along the length of the solenoid. A higher number of turns per meter increases the magnetic field strength inside the solenoid, enhancing its magnetic properties.
How is the torque on a current-carrying loop in a magnetic field calculated?
-The torque on a current-carrying loop in a magnetic field is calculated using the formula τ = n × I × A × B × sin(θ), where n is the number of loops, I is the current, A is the area of the loop, B is the magnetic field strength, and θ is the angle between the loop’s plane and the magnetic field direction.
Outlines
🧲 Basic Principles of Magnetism
This paragraph introduces the fundamental concepts of magnetism, including the interaction between the poles of bar magnets, the repulsion and attraction phenomena, and the existence of magnetic fields around magnets. It explains how like poles repel each other while opposite poles attract. The concept of a magnetic field, which is created by moving electric charges, is also introduced, with an example of how an electric current in a wire generates a circular magnetic field. The right-hand rule is mentioned as a method to determine the direction of the magnetic field around a current-carrying wire.
📐 Calculating Magnetic Field Strength
The paragraph discusses the mathematical formula to calculate the strength of the magnetic field created by a current-carrying wire. It explains the relationship between the current, the permeability of free space (μ0), the distance from the wire (r), and the strength of the magnetic field (B). The concept of directly and inversely related variables in the formula is also explained, along with the illustration of how the strength of the magnetic field changes with distance and current.
🤝 Forces on Current-Carrying Wires in Magnetic Fields
This section explores the forces exerted on a current-carrying wire when it is placed in a magnetic field. It explains that a magnetic field does not exert a force on a stationary charge but does exert a force on moving charges, such as those in an electric current. The force experienced by the wire is calculated using the equation F = i * l * B * sin(θ), where i is the current, l is the length of the wire, B is the magnetic field strength, and θ is the angle between the current and the magnetic field. The right-hand rule is used to determine the direction of the force.
⚙️ Torque on a Current-Carrying Loop
The paragraph explains the concept of torque on a current-carrying loop placed in a magnetic field. It describes how the magnetic field exerts a force on the loop, causing it to rotate. The torque is calculated using the equation T = n * I * A * B * sin(θ), where n is the number of loops, I is the current, A is the area of the loop, and B is the magnetic field strength. The magnetic dipole moment (magnetization) is also introduced as a product of the number of loops, current, and area.
🔍 Ampere's Law and Solenoids
This section delves into Ampere's Law, which relates the magnetic field around a closed loop to the current passing through the loop. The law is used to derive the formula for the magnetic field created by a solenoid, which is a device made of many loops of wire that can produce a strong magnetic field. The magnetic field inside a solenoid is shown to be proportional to the current, the number of turns per unit length, and inversely proportional to the length of the solenoid.
🔗 Force Between Parallel Wires
The paragraph discusses the force between two parallel wires carrying current. It explains that wires with currents in the same direction will attract each other, while wires with currents in opposite directions will repel each other. The magnitude of the force between the wires is calculated using the formula F = μ0 * I1 * I2 * L / (2πr), where μ0 is the permeability of free space, I1 and I2 are the currents in the wires, L is the length of the wires, and r is the distance between them.
🏗️ Deriving the Magnetic Field of a Solenoid
This section focuses on deriving the formula for the magnetic field inside a solenoid using Ampere's Law. It explains that the magnetic field is strongest inside the solenoid and that the contribution to the magnetic field from segments outside the solenoid is negligible. The enclosed current is considered, which increases with the number of loops in the solenoid. The final formula derived is B = μ0 * n * I, where n is the number of turns per unit length.
🧭 Magnetic Field and Torque on a Loop
The paragraph explores the magnetic field's effect on a current-carrying loop, which results in the loop experiencing a torque. It explains how the forces on opposite sides of the loop are equal and opposite, leading to a net torque that causes the loop to rotate. The torque is maximized when the magnetic field is perpendicular to the normal line of the loop, and it is zero when the magnetic field is parallel to the normal line.
🔧 Solving Problems Involving Torque and Magnetic Fields
This section presents problems involving the calculation of torque on a current-carrying coil in a magnetic field. It demonstrates how to use the formula for torque, which includes the number of loops, current, area of the loop, and the magnetic field strength. The problems require converting units and applying the formula to find either the maximum torque for a given magnetic field or the required magnetic field strength to achieve a certain torque.
Mindmap
Keywords
💡Magnetism
💡Magnetic Field
💡Right-Hand Rule
💡Ampere's Law
💡Solenoid
💡Magnetic Force
💡Permeability of Free Space (μ0)
💡Magnetic Dipole Moment
💡Torque
💡Electric Current
💡Magnetic Flux Density (B)
Highlights
Magnetism involves the interaction between magnetic poles, with like poles repelling and opposite poles attracting.
Every bar magnet has its own magnetic field that emanates from the north pole and travels towards the south pole.
The magnetic field around a wire carrying an electric current is circular and can be determined using the right-hand rule.
The strength of the magnetic field created by a wire is calculated using the equation B = μ₀ * I / (2πr), where B is the magnetic field, μ₀ is the permeability of free space, I is the current, and r is the distance from the wire.
The magnetic force on a current-carrying wire in a magnetic field is given by F = I * L * B * sin(θ), where F is the force, I is the current, L is the length of the wire in the magnetic field, B is the magnetic field strength, and θ is the angle between the current and the magnetic field.
The magnetic force on a moving point charge can be calculated using F = q * v * B * sin(θ), where q is the charge, v is the velocity, and θ is the angle between the velocity and the magnetic field.
The direction of the magnetic force on a moving charge can be found using the right-hand rule, with the thumb pointing in the direction of the charge's velocity and the fingers pointing in the direction of the magnetic field.
A charged particle moving in a magnetic field experiences a force that acts as a centripetal force, causing the particle to move in a circular path.
The radius of the circular path of a charged particle in a magnetic field can be calculated using r = m * v / (q * B), where m is the mass of the particle, v is its velocity, q is its charge, and B is the magnetic field strength.
The kinetic energy of a moving proton can be converted to electron volts (eV), with 1 eV equal to 1.6 x 10^-19 joules.
Parallel wires carrying currents in the same direction will attract each other, while those with currents in opposite directions will repel.
Ampere's Law relates the magnetic field around a closed loop to the current enclosed by the loop, with B * 2πr = μ₀ * I, where B is the magnetic field, r is the radius of the loop, I is the current, and μ₀ is the permeability of free space.
The magnetic field strength inside a solenoid can be calculated using B = μ₀ * n * I, where n is the number of turns per unit length.
The torque experienced by a current-carrying loop in a magnetic field is given by τ = N * I * A * B * sin(θ), where N is the number of loops, I is the current, A is the area, and θ is the angle between the magnetic field and the normal to the loop.
The magnetic dipole moment (μ) is defined as the product of the number of loops, current, and area (μ = N * I * A).
The maximum torque on a current-carrying loop occurs when the magnetic field is perpendicular to the normal of the loop's plane.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: