Kinematics (AP Physics SuperCram Review)

We Are Showboat
28 Apr 201203:39
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the principles of kinematics, emphasizing their applicability to scenarios with constant acceleration. It clarifies the use of kinematic formulas for moving cars, balls rolling down hills, and projectiles, highlighting the importance of distinguishing between positive and negative vectors. The script also addresses the unique considerations for 2D kinematics, such as separating horizontal and vertical components and the constant horizontal acceleration of a projectile. It concludes with an exploration of motion graphs, illustrating how slopes and curvatures indicate velocity and acceleration, and the significance of understanding the direction of motion and acceleration.

Takeaways
  • 📚 Kinematic formulas are applicable only when acceleration is constant.
  • 🚗 Cars and balls moving with constant acceleration can be analyzed using kinematic equations.
  • 🚫 Simple harmonic oscillators, like a mass on a spring, do not use these formulas due to varying acceleration.
  • 🎯 Displacement is represented by (X - X_0), initial velocity by (V_0), and acceleration by (a).
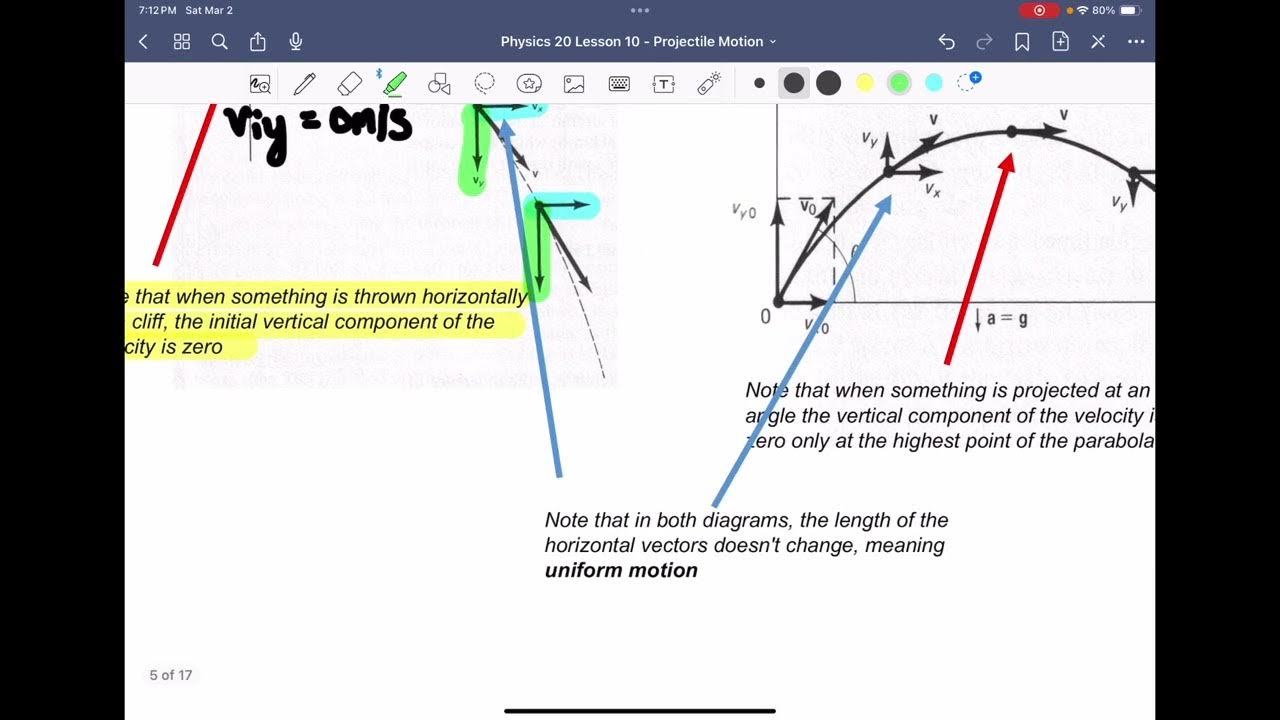
  • 🏞 Projectile motion at peak height has zero velocity in the y-direction but not zero acceleration; it's negative at 9.8 m/s^2.
  • 💥 When an object hits the ground, its final velocity is not zero, indicating ongoing motion until impact.
  • 📊 In 2D kinematics, horizontal and vertical motions must be analyzed separately with appropriate components.
  • 🌐 For horizontal projectile motion, the acceleration is zero, meaning horizontal velocity (V_x) is constant.
  • 📉 The acceleration in the y-direction during projectile motion is always negative, indicating a constant change in vertical velocity.
  • 📈 The range formula is useful for projectile motion when the vertical displacement is zero, implying the start and end height are the same.
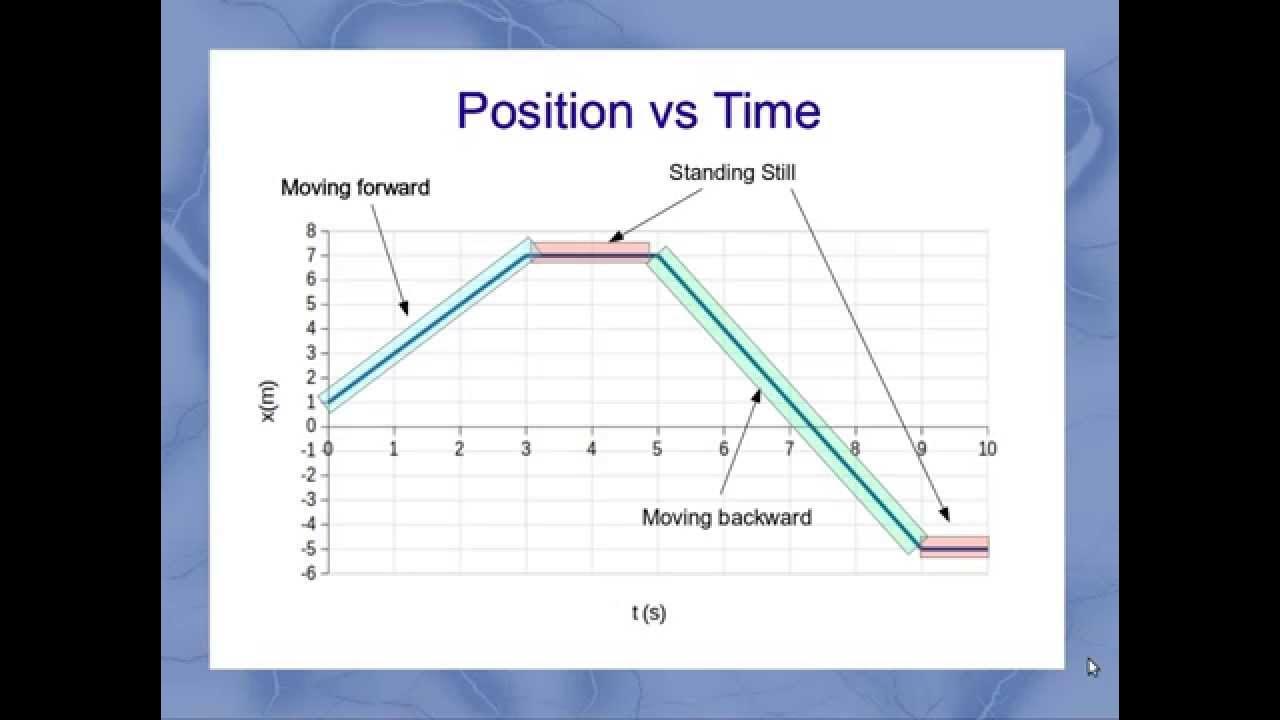
  • 📊 Graphs of motion, such as position vs. time, show velocity as the slope, and changes in slope indicate acceleration.
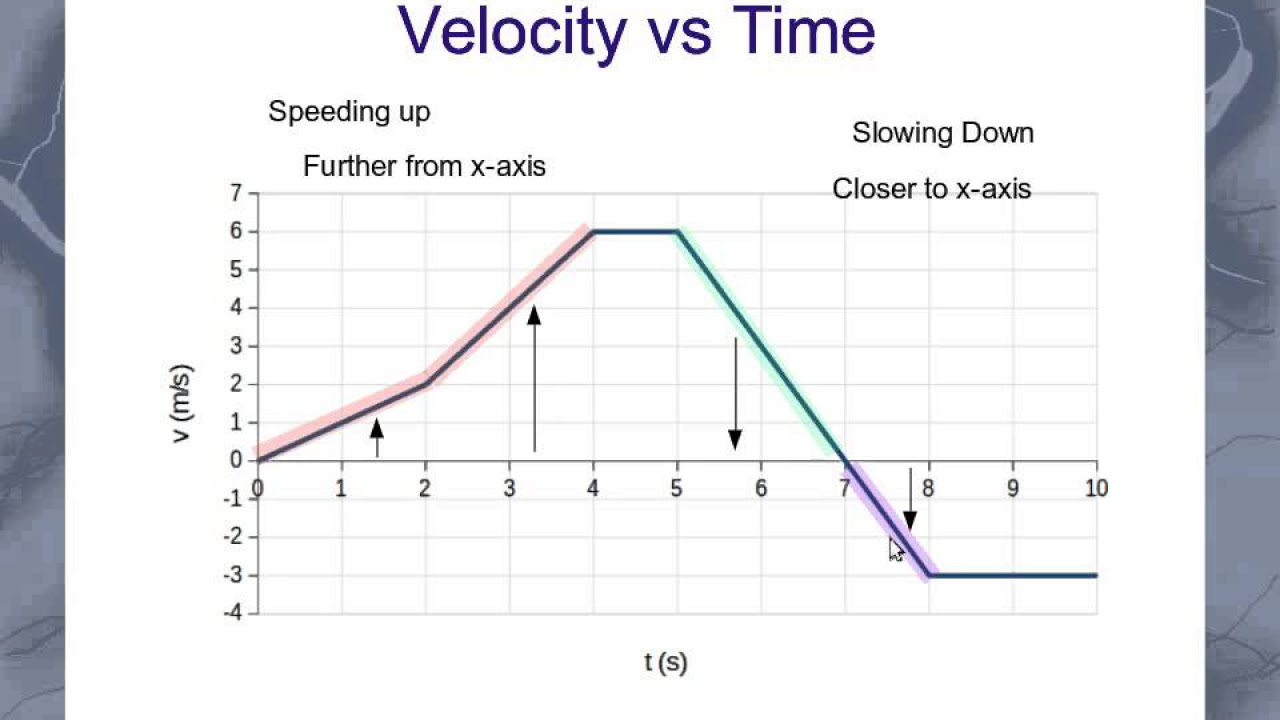
  • 🔍 On velocity vs. time graphs, the slope represents acceleration, and moving towards or away from the time axis indicates slowing down or speeding up, respectively.
Q & A

  • What are the conditions under which kinematic formulas can be used?

    -Kinematic formulas can be used when the acceleration is constant, such as in the case of a car moving forward with a constant rate of acceleration or deceleration, or a ball moving down a hill with constant acceleration.

  • Why can't kinematic formulas be used for a simple harmonic oscillator?

    -For a simple harmonic oscillator, the acceleration is not constant, which makes the kinematic formulas inapplicable.

  • What does the term 'X minus X naught' represent in kinematics?

    -'X minus X naught' represents the displacement of an object in kinematics, where X is the final position and X naught is the initial position.

  • What is the initial velocity denoted by in kinematic formulas?

    -The initial velocity in kinematic formulas is denoted by 'V naught'.

  • At the peak height of a projectile, is the velocity zero?

    -No, at the peak height of a projectile, the velocity in the vertical direction is zero for a split second, but the horizontal velocity remains constant.

  • What is the acceleration of a projectile at its peak height?

    -At the peak height, the acceleration is not zero; it is negative 9.8 meters per second squared, directed downwards.

  • How should the motion of a projectile be analyzed in 2D kinematics?

    -In 2D kinematics, the horizontal and vertical motions should be analyzed separately. The initial velocity should be broken down into X and Y components, and the appropriate kinematic equations should be applied to each component separately.

  • What is the horizontal acceleration for a projectile in motion?

    -The horizontal acceleration for a projectile in motion is always zero, meaning the horizontal velocity remains constant throughout its trajectory.

  • Is the acceleration in the y-direction zero at the peak height of a projectile?

    -No, the acceleration in the y-direction is not zero at the peak height; it is always negative 9.8 m/s^2, indicating a constant downward acceleration.

  • What is the significance of the range formula in projectile motion?

    -The range formula can be useful in projectile motion when the vertical displacement is zero, meaning the object ends at the same height it started from.

  • How can a position versus time graph help in understanding motion?

    -A position versus time graph can indicate the velocity of an object, as the slope of the graph represents the velocity. Positive slope indicates forward motion, negative slope indicates backward motion, and zero slope indicates the velocity is zero. Changes in slope indicate acceleration.

  • What does the slope on a velocity versus time graph represent?

    -On a velocity versus time graph, the slope represents the acceleration of the object. A positive slope indicates positive acceleration, a negative slope indicates negative acceleration, and a zero slope means there is no acceleration.

  • What does it mean if an object is moving towards or away from the time axis on a velocity graph?

    -If an object is moving towards the time axis on a velocity graph, it is slowing down. If it is moving away from the time axis, it is speeding up, regardless of whether the acceleration is negative or positive.

Outlines
00:00
📚 Kinematic Formulas and Their Applicability

This paragraph discusses the conditions under which kinematic formulas can be applied, specifically when acceleration is constant. It covers scenarios such as a car moving with constant acceleration or deceleration, a ball rolling down a hill, and a simple harmonic oscillator where the acceleration varies. The paragraph also clarifies misconceptions about acceleration at the peak of a projectile's trajectory and emphasizes the importance of considering vectors' direction in 2D kinematics. It explains the separation of horizontal and vertical motion for projectile motion, noting that horizontal acceleration is zero, and vertical acceleration is consistently negative due to gravity.

📉 Understanding Graphs in Kinematics

The second paragraph focuses on interpreting graphs in kinematics, explaining how to analyze motion through position versus time and velocity versus time graphs. It describes how the slope of these graphs represents velocity and acceleration, respectively, and how to interpret positive and negative slopes. The paragraph uses an example graph to illustrate an object's motion, starting with constant velocity, slowing down, reversing direction, and eventually coming to a stop. It also cautions about misinterpreting negative acceleration as slowing down and positive acceleration as speeding up, depending on the context of the motion.

Mindmap
Keywords
💡Kinematic Formulas
Kinematic formulas are mathematical equations used to describe the motion of an object when certain variables like initial velocity, acceleration, and time are known. In the context of the video, these formulas are applicable when acceleration is constant, which is crucial for analyzing scenarios like a car moving at a constant rate or a ball rolling down a hill.
💡Constant Acceleration
Constant acceleration refers to the rate of change of velocity that does not vary over time. It is a fundamental concept in the video, as it dictates when kinematic formulas can be used. For instance, the video mentions that if a car is speeding up or slowing down at a constant rate, kinematic formulas are applicable.
💡Displacement
Displacement is the vector that represents the change in position of an object from its initial to its final position. The video script uses 'X minus X naught' to denote the displacement, emphasizing that it is a vector quantity with both magnitude and direction.
💡Velocity
Velocity is the speed of an object in a particular direction. The video explains that velocity can be initial (V naught) or at a certain time (V), and it is a key variable in kinematic equations. The script also clarifies that at the peak height of a projectile, the velocity is momentarily zero.
💡Acceleration
Acceleration is the rate at which an object's velocity changes over time. The video points out that for simple harmonic motion, acceleration is not constant, hence different formulas are needed. However, for objects like a ball rolling down a hill or a car moving at a constant rate, acceleration is constant and can be described with kinematic formulas.
💡Projectile Motion
Projectile motion is the motion of an object thrown or projected into the air, subject to only the acceleration due to gravity. The video script discusses the characteristics of projectile motion, such as the velocity being zero at the peak and the constant acceleration of gravity acting downwards.
💡2D Kinematics
2D kinematics involves analyzing motion in two dimensions, typically horizontal and vertical. The video script explains that for projectile motion, one must separate the horizontal and vertical components of motion and apply kinematic formulas to each separately, as horizontal acceleration is zero while vertical acceleration is due to gravity.
💡Range Formula
The range formula is a specific kinematic equation used to calculate the horizontal distance traveled by a projectile, given certain initial conditions. The video script notes that this formula is only applicable when the vertical displacement is zero, meaning the projectile lands at the same height from which it was launched.
💡Graphing Motion
Graphing motion involves plotting position, velocity, or acceleration against time to visualize an object's motion. The video script explains how to interpret such graphs, including understanding slopes as velocities, changes in slope as accelerations, and curvature as an indication of non-uniform acceleration.
💡Acceleration Vector
An acceleration vector is a vector quantity that not only has a magnitude (the rate of change of velocity) but also a direction. The video script emphasizes that acceleration can be positive or negative, indicating the direction of the change in velocity, such as upwards or downwards.
💡Negative Acceleration
Negative acceleration, also known as deceleration, is when the acceleration vector points in the opposite direction to the velocity vector, causing the object to slow down. The video script clarifies that negative acceleration does not necessarily mean the object is moving backwards, just that it is slowing down.
Highlights

Kinematic formulas can only be used with constant acceleration.

Examples of constant acceleration include a car moving forward at a constant rate and a ball rolling down a hill.

Simple harmonic oscillators do not have constant acceleration and thus cannot use these formulas.

At the peak height of a projectile, the velocity is zero, but the acceleration is not.

The acceleration at the peak of a projectile is negative, at 9.8 m/s², and is directed downwards.

The final velocity of an object before hitting the ground is not zero.

Vectors in kinematics can be positive or negative, and the negative sign is crucial for understanding motion direction.

For 2D kinematics, horizontal and vertical motions must be analyzed separately.

In 2D kinematics, the horizontal acceleration for a projectile is always zero, maintaining constant horizontal velocity.

The vertical acceleration in projectile motion is always negative 9.8 m/s², indicating a constant change in vertical velocity.

The range formula is useful for projectile motion with zero vertical displacement, meaning the start and end heights are the same.

Graphing motion involves understanding that the slope of a position-time graph represents velocity.

Curvature on a graph is a clear indication of acceleration.

On a velocity-time graph, the slope represents acceleration, where a positive slope indicates positive acceleration.

A velocity graph where the object moves towards the time axis indicates slowing down, while moving away indicates speeding up.

Understanding the direction of acceleration is essential, as negative acceleration does not always mean slowing down.

The transcript provides a detailed example of an object's motion, including starting, slowing, reversing, and maintaining constant velocities.

Transcripts

Browse More Related Video

Interpreting Motion Graphs

Projectile Motion - AP Physics 1: Kinematics Review Supplement

AP Physics 1 | Unit 1: Kinematics

Interpreting Velocity graphs

AP Physics 1 review of 2D motion and vectors | Physics | Khan Academy

Physics 20 Unit A Lesson 10: Projectile Motion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
KinematicsProjectile MotionConstant AccelerationPhysicsMotion GraphsVelocityDisplacementAcceleration2D MotionScience Education