AP Physics 1 review of 2D motion and vectors | Physics | Khan Academy
TLDRThe video script delves into the concept of vector components, explaining how they represent the perpendicular pieces of any vector, typically along the X and Y axes. It outlines the mathematical relationship between the magnitude of a vector, the angle it makes, and its components using sine and cosine functions. The script also introduces the method of tail-to-tip vector addition, a graphical technique for summing vectors, and contrasts it with the more mathematical component-wise addition. Furthermore, the script explores 2D kinematics, particularly focusing on projectile motion where vertical and horizontal components behave independently, with constant vertical acceleration due to gravity. It provides a formula for calculating the horizontal displacement of a projectile and discusses the importance of graphing data to a linear fit for determining experimental values, such as the acceleration due to gravity, using the slope of the best-fit line. The summary encapsulates the instructional nature of the script, highlighting its aim to educate viewers on vector mathematics and kinematics through clear explanations and examples.
Takeaways
- 📚 Vector components represent the separation of a vector into perpendicular parts, typically along the X and Y axes.
- 📐 The vertical component of a vector can be found using the formula: magnitude * sine of the angle.
- 📏 The horizontal component of a vector is calculated as: magnitude * cosine of the angle.
- 🔄 The signs of vector components depend on the direction of the vector: positive for right and up, negative for left and down.
- 🔍 Tail-to-tip vector addition involves placing the tail of one vector at the tip of another to find the resultant vector.
- 🔬 In vector addition, the total vector can also be found by adding the individual horizontal and vertical components.
- 🚀 2D kinematics problems, such as projectile motion, involve objects moving through the air at angles with constant vertical acceleration due to gravity.
- 📉 Projectiles have no horizontal acceleration, meaning the horizontal velocity component remains constant throughout the motion.
- 📈 To solve for unknowns in projectile motion, use separate kinematic equations for the horizontal and vertical components.
- 📊 Graphing data to a linear fit involves plotting variables in such a way that the relationship between them forms a straight line, simplifying the determination of the slope.
- 🧭 An example of graphing to a linear fit includes plotting the distance a ball travels (Y) versus its speed squared (X) to experimentally determine the acceleration due to gravity.
Q & A
What are vector components?
-Vector components are a method of breaking down any vector into two perpendicular pieces, typically along the X and Y directions.
How do you find the vertical component of a vector given an angle?
-The vertical component can be found by multiplying the magnitude of the total vector by the sine of the given angle.
How is the horizontal component of a vector related to the angle?
-The horizontal component is found by multiplying the magnitude of the total vector by the cosine of the angle, as it is adjacent to the angle.
What is the significance of sine and cosine in determining vector components?
-Sine is used to find the component opposite to the angle, while cosine is used to find the component adjacent to the angle.
How do you determine the direction of vector components?
-If the vector points right, the horizontal component is positive; if left, it's negative. If the vector points up, the vertical component is positive; if down, it's negative.
What is tail to tip or head to tail vector addition?
-Tail to tip or head to tail vector addition is a graphical method to add or subtract vectors by placing the tail of one vector at the tip of another, then drawing the total vector from the first tail to the last head.
How can you mathematically add vectors?
-You can mathematically add vectors by adding up their individual horizontal and vertical components separately.
What is the role of vertical acceleration in 2D kinematics problems?
-In 2D kinematics problems, the vertical acceleration is constant at -9.8 m/s² (due to gravity) and there is no horizontal acceleration, allowing the X and Y components to behave independently.
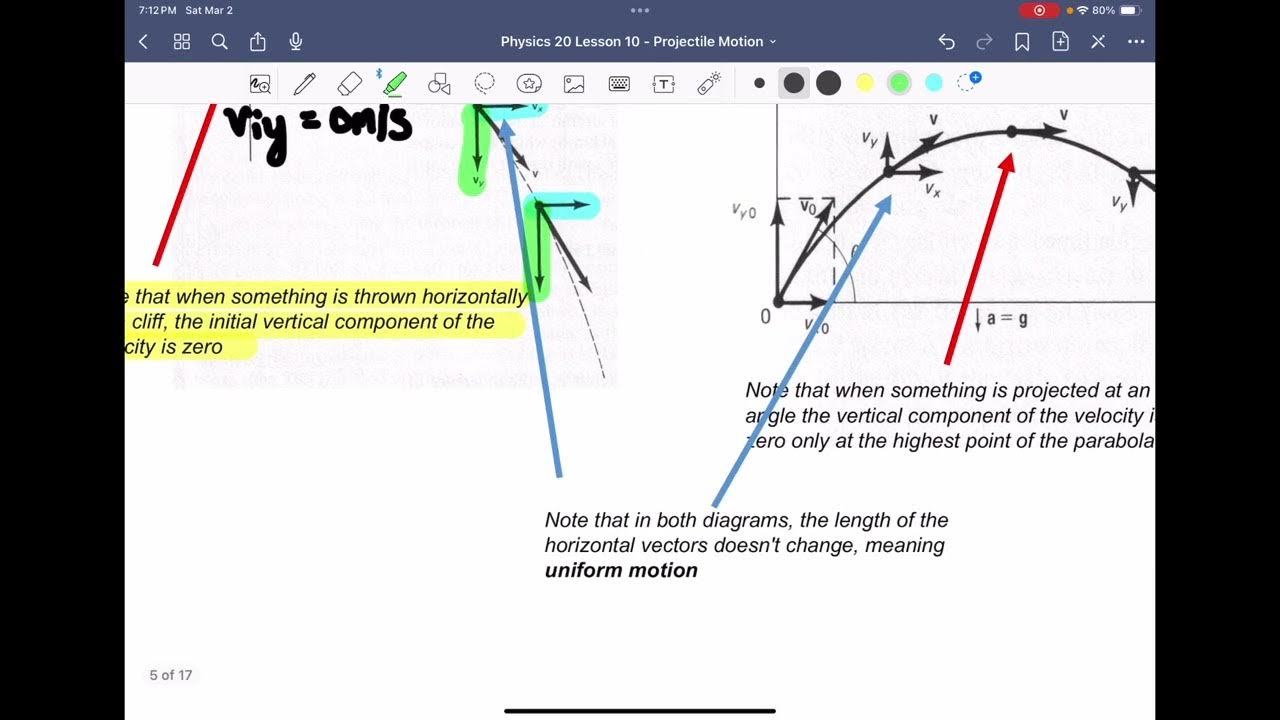
How does the vertical component of velocity change during a projectile's flight?
-The vertical component of velocity decreases as the projectile rises until it reaches the peak, becomes zero at the peak, and then increases in the negative direction as the projectile descends.
What is the formula for determining the horizontal distance a projectile travels before hitting the ground?
-The horizontal distance can be determined by multiplying the horizontal velocity (V) by the time of flight (T), which can be found using the vertical displacement and acceleration due to gravity.
How can you graph data to a linear fit?
-To graph data to a linear fit, you need to express the relationship between variables in the form of a straight line (Y = M*X + B), where Y is the dependent variable, X is the independent variable, M is the slope, and B is the Y-intercept.
How can you experimentally determine the acceleration due to gravity using a ball rolling off a table?
-By plotting the horizontal distance traveled by the ball (delta X) against the initial speed (V) or another variable derived from the motion equation that results in a linear relationship, you can determine the slope of the best fit line, which can then be used to solve for the acceleration due to gravity (G).
Outlines
📚 Understanding Vector Components
The first paragraph explains the concept of vector components, which are a method to decompose any vector into two perpendicular parts typically aligned with the X and Y axes. The vertical component is calculated as the total vector's magnitude multiplied by the sine of the angle, while the horizontal component is the magnitude times the cosine of the angle. The explanation clarifies the use of sine for opposite sides and cosine for adjacent sides in relation to the angle. An example problem is provided to illustrate the calculation of the X and Y components of a velocity vector, emphasizing the importance of including direction (positive or negative) in the calculation. The paragraph also introduces tail-to-tip vector addition, a graphical technique for adding or subtracting vectors by connecting the tail of one vector to the head of another, culminating in a total vector drawn from the first tail to the last head.
📐 Vector Addition and 2D Kinematics
The second paragraph delves into the mathematical approach to vector addition by summing individual horizontal and vertical components. It demonstrates how to find the total vector by adding the respective components of two vectors, A and B, and explains the significance of direction in determining the sign of the components. The paragraph then transitions into discussing 2D kinematics, specifically projectile motion, where objects move through the air at angles and are subject to gravity, causing vertical acceleration of -9.8 m/s² with no horizontal acceleration. The independent behavior of X and Y components is highlighted, with different kinematic equations applied to each. The example of a meatball rolling off a table is used to illustrate how to calculate horizontal displacement before striking the floor, using given quantities and fundamental constants like gravity (G).
📉 Graphing Data to a Linear Fit
The third paragraph focuses on the technique of graphing data to achieve a linear fit, which simplifies the process of determining the slope of a graph. It explains that data does not always plot linearly, and when it does not, finding the slope can be challenging. The solution is to express the relationship between data variables in the form of a straight line, Y = Mx + B, where Y is the dependent variable, X is the independent variable, M is the slope, and B is the Y-intercept. An example is given where plotting P versus D² results in a straight line, allowing for easy slope determination. The paragraph further explores the concept with an example problem involving rolling a sphere off a table at varying speeds and measuring the distance traveled before impact. It guides through the process of plotting the correct variables to linearize the data and using the slope of the best-fit line to experimentally determine the acceleration due to gravity (G), given a known table height (H).
Mindmap
Keywords
💡Vector Components
💡Magnitude
💡Trigonometry
💡Direction
💡Vector Addition
💡Tail to Tip
💡2D Kinematics
💡Acceleration
💡Projectile Motion
💡Graphing Data
💡Linear Fit
Highlights
Vector components are a method of breaking any vector into two perpendicular pieces.
Typically, vector components are chosen to lie along the X and Y directions.
The vertical component of a vector can be found using the magnitude times sine of the angle.
The horizontal component is found using the magnitude times cosine of the angle.
For different angles, the roles of sine and cosine are swapped to find vector components.
To find the opposite side of a right triangle, use sine, and for the adjacent side, use cosine.
An example problem involving vector components includes determining the X and Y components of a velocity vector.
The horizontal component is positive if the vector points right, and negative if it points left.
The vertical component is positive if the vector points up, and negative if it points down.
Tail to tip or head to tail vector addition is a graphical method for adding or subtracting vectors.
The process involves placing the tail of one vector at the tip of another to find the total vector.
Vector subtraction can be achieved by adding the negative of the vector to be subtracted.
An example of tail to tip vector addition involves adding multiple vectors to find the total direction.
Vector addition can also be performed mathematically by adding up individual components.
For 2D kinematics problems, vertical and horizontal components behave independently.
In 2D kinematics, the vertical acceleration is constant at -9.8 m/s², with no horizontal acceleration.
A projectile's horizontal velocity remains constant throughout its flight due to zero horizontal acceleration.
The vertical component of velocity decreases until reaching the top of the trajectory and increases on the way down.
An example 2D kinematics problem involves calculating the horizontal distance a meatball travels after rolling off a table.
Graphing data to a linear fit involves plotting variables in a way that their relationship forms a straight line.
Forcing a non-linear relationship into a linear graph allows for easier determination of the slope.
An example of graphing data to a linear fit includes determining the experimental value for gravity's acceleration.
By plotting the correct variables, one can linearize the relationship and solve for unknown constants like gravity.
Transcripts
Browse More Related Video
Physics 20 Unit A Lesson 10: Projectile Motion

AP Physics B Kinematics Presentation General Problems #08

Vector components from magnitude and direction
Where Does The Range Equation Come From?

17 - Calculating Vector Components in Physics, Part 1 (Component form of a Vector)
2. Vectors in Multiple Dimensions
5.0 / 5 (0 votes)
Thanks for rating: