2021 Live Review 7 | AP Physics C: Mechanics | Angular Momentum & Rotational Collisions

Advanced Placement

28 Apr 202140:26

EducationalLearning

32 Likes 10 Comments

TLDRThis video script from an AP Daily Live Review for Physics C Mechanics delves into the principles of angular momentum, particularly in rotating and linearly moving objects. It covers the conservation of angular momentum under zero external torques and explores rotational collisions, including elastic and inelastic scenarios. The script provides step-by-step problem-solving techniques for calculating angular momentum and discusses the implications of conservation laws on kinetic energy during collisions. It also offers multiple-choice questions to reinforce the concepts discussed.

Takeaways

📚 Angular momentum is a vector quantity, distinct from rotational inertia which is a scalar, and angular velocity which is also a vector.
🔍 For an object moving in a straight line, the angular momentum is calculated using the cross product of the position vector (r) and the linear momentum (p = mv).
📐 The perpendicular distance from the axis of rotation to the velocity vector (r sine theta) is a crucial component in determining angular momentum, simplifying calculations.
🚫 Conservation of angular momentum occurs when the sum of external torques acting on a system is zero, akin to linear momentum conservation when the sum of external forces is zero.
💥 In elastic collisions, both translational and rotational kinetic energies are conserved, while in inelastic collisions, kinetic energy can decrease and objects may separate post-collision.
🔄 Rotational inertia represents an object's resistance to changes in its rotation, being a measure of how difficult it is to initiate or stop rotation.
🧩 In perfectly inelastic collisions, objects stick together after the collision, which is a subset of inelastic collisions where kinetic energy is not conserved.
🌟 The video script provides a step-by-step example of calculating angular momentum and velocity for a rod and ball system, emphasizing the importance of conservation laws.
🛰️ An astronaut in orbit throwing a ball at an assembly is used as an example to illustrate the principles of angular momentum conservation and the calculation of kinetic energy changes.
❓ The script poses multiple-choice questions to test understanding, highlighting the importance of reading questions carefully and applying conservation principles correctly.
🎯 The final takeaway emphasizes the importance of understanding the conservation of both linear and angular momentum in scenarios involving frictionless surfaces and systems in orbit.

Q & A

What is angular momentum and why is it considered a vector?
-Angular momentum is a measure of the quantity of rotation of an object and is represented by the cross product of the position vector and the momentum of the object. It is considered a vector because it has both magnitude and direction, and it follows the right-hand rule for direction.
How does one calculate the angular momentum of an object moving in a straight line?
-The angular momentum of an object moving in a straight line is calculated using the cross product of the position vector (r) from the origin to the object and the linear momentum of the object (p). It can be simplified by using the perpendicular distance from the origin to the velocity vector (r * sin(theta)) multiplied by the linear momentum.
What is the condition for the conservation of angular momentum?
-Angular momentum is conserved when the sum of the external torques acting on a system is zero. This means that there are no external forces causing a torque that would change the angular momentum of the system.
How is rotational inertia related to angular momentum?
-Rotational inertia is a scalar quantity that represents an object's resistance to changes in its rotation. It is used in the formula for angular momentum of a rotating object, which is the product of the rotational inertia (I) and the angular velocity (ω).
What is the difference between elastic and inelastic collisions in terms of kinetic energy?
-In elastic collisions, the total kinetic energy of the system is conserved, meaning it remains the same before and after the collision. In inelastic collisions, some of the kinetic energy is converted into other forms of energy, such as heat or sound, resulting in a decrease in the total kinetic energy of the system.
What is a perfectly inelastic collision and how does it differ from other inelastic collisions?
-A perfectly inelastic collision is a special type of inelastic collision where the objects involved stick together after the collision. In contrast to other inelastic collisions, where the objects may move apart after the collision, in a perfectly inelastic collision, the kinetic energy loss is maximized, and the objects move as one unit after the collision.
How can one determine the distance from the left ball to the center of mass after a collision in a system?
-The distance from the left ball to the center of mass after a collision can be determined using the formula for the center of mass, which is the sum of the product of each mass and its position, divided by the total mass of the system. This calculation takes into account the positions of all masses involved and their respective masses.
What is the effect of a perfectly inelastic collision on the kinetic energy of a system?
-In a perfectly inelastic collision, the kinetic energy of the system decreases because some of the energy is converted into other forms, such as heat or sound. The system loses energy, and this is reflected in a negative change in kinetic energy.
How does the conservation of linear momentum apply to a system where a skater jumps off a rotating platform?
-In a system where a skater jumps off a rotating platform, the conservation of linear momentum applies because there are no external forces acting on the system in the horizontal direction. The initial linear momentum of the system is equal to the final linear momentum after the skater jumps off.
What is the relationship between the angular speed of a rotating system and the conservation of angular momentum?
-The angular speed of a rotating system is related to the conservation of angular momentum by the fact that if no external torques are acting on the system, the angular momentum remains constant. If the rotational inertia of the system changes, such as when an object is added or removed, the angular speed will adjust accordingly to maintain the same total angular momentum.

Outlines

00:00

🚀 Introduction to Angular Momentum and Conservation Laws

The paragraph introduces the concept of angular momentum, its vector nature, and the difference between rotational inertia and angular velocity. It sets the stage for a discussion on rotational collisions, conservation of angular momentum, and the calculation methods for both rotating and straight-line moving objects. The presenter suggests watching specific AP Daily videos for foundational knowledge and emphasizes the importance of understanding the cross product of position vector 'r' and linear momentum for calculating angular momentum in straight-line motion. The conditions for angular momentum conservation are also discussed, relating it to the absence of external torques.

05:02

📚 Analyzing Rotational Inertia and Collision Dynamics

This section delves into a problem involving a rod on a horizontal, frictionless table, emphasizing the conservation of angular momentum due to the absence of external torques. The paragraph explains how to calculate the angular momentum of the rod before a collision with a ball and then determines the speed of the ball after the collision, using the principles of angular momentum conservation. It also explores the concept of elastic and inelastic collisions, including perfectly inelastic collisions where objects stick together post-impact, and how these affect kinetic energy.

10:02

🌌 Space Dynamics: Collisions and Angular Momentum in Orbit

The paragraph presents a scenario involving an astronaut in a circular orbit around Earth with an assembly of two spheres connected by a rod. It discusses a collision where a ball of clay sticks to the assembly, and the system's total kinetic energy post-collision is to be determined. The conservation of linear and angular momentum in the absence of external forces is highlighted, and the problem of calculating the change in kinetic energy due to the collision is tackled, revealing a loss in kinetic energy indicative of an inelastic collision.

15:03

🎯 Collision Outcomes and Center of Mass Calculations

This section continues the theme of collisions but focuses on determining the distance from the left ball to the center of mass immediately after a collision and the direction of motion of the center of mass. The conservation of linear momentum and the calculation of the center of mass using a weighted average of the positions of the masses are discussed. The paragraph also addresses the speed of the center of mass post-collision and the angular speed of the system, incorporating the concept of rotational inertia about the center of mass.

20:04

🛹 Ice Skater Physics: Angular Momentum Conservation on a Frictionless Surface

The paragraph explores a thought experiment involving a long board on frictionless ice and a skater who jumps on one end, causing the board to slide and rotate. It presents multiple-choice questions that test the understanding of the conservation of linear and angular momentum, leading to the conclusion that both are conserved due to the frictionless nature of the scenario. The discussion also touches on the transformation of kinetic energy between translational and rotational forms.

25:05

🎲 Collisions and Conservation Laws in Multiple Choice Format

This section presents a multiple-choice question format to illustrate the application of conservation laws during collisions. It covers scenarios such as a disc colliding with a rod and a student on a rotating platform throwing a rock. The importance of reading questions carefully and understanding the implications of frictionless conditions on the conservation of linear and angular momentum is emphasized. The paragraph also discusses the implications of elastic and inelastic collisions on kinetic energy.

30:06

🤸‍♂️ Student on a Rotating Platform: Angular Momentum and Its Conservation

The paragraph describes a scenario where a student on a frictionless rotating platform throws a rock tangentially, affecting the platform's angular speed. It explains the conservation of angular momentum in a frictionless system and how the initial angular momentum of the system is zero. The problem involves deriving an expression for the angular speed of the platform after the rock is thrown, taking into account the distribution of masses and their distances from the axis of rotation.

35:10

🔄 Angular Momentum and Its Conservation in Various Scenarios

The final paragraph wraps up the discussion by summarizing key points about angular momentum, its conservation, and its calculation in different scenarios. It reiterates the importance of understanding the perpendicular distance from the axis of rotation to the velocity vector and the conditions under which angular momentum is conserved. The paragraph also touches on the differences between elastic and inelastic collisions, particularly perfectly inelastic collisions where objects stick together after the collision.

Mindmap

Keywords

💡Angular Momentum

Angular momentum is a vector quantity that represents the product of an object's moment of inertia and its angular velocity. It is a fundamental concept in the video, as it is used to explain how the motion of objects, whether rotating or moving in a straight line, can be analyzed. In the script, angular momentum is used to describe the motion of objects before and after collisions, emphasizing its conservation when no external torques are acting on a system.

💡Rotational Inertia

Rotational inertia, also known as the moment of inertia, is a scalar quantity that describes an object's resistance to changes in its rotation. It is defined by the mass distribution of the object and its distance from the axis of rotation. In the video, rotational inertia is used to calculate angular momentum for a rotating object and is a key factor in determining the outcome of rotational collisions.

💡Angular Velocity

Angular velocity is a vector quantity that represents the rate of change of an angle over time. It is used in the video to describe how fast an object is rotating. The script mentions angular velocity in the context of calculating angular momentum (iω) and in discussions of rotational kinetic energy.

💡Linear Momentum

Linear momentum is the product of an object's mass and its velocity, and it is a vector quantity. The video script explains that the angular momentum of an object moving in a straight line can be found using the cross product of the position vector and the linear momentum. It is also discussed in the context of conservation during collisions where no external forces are present.

💡Torque

Torque is the rotational equivalent of force and is responsible for producing rotational motion. In the video, torque is discussed in the context of angular momentum conservation, stating that if the sum of torques acting on a system is zero, the angular momentum of the system is conserved.

💡Elastic Collisions

Elastic collisions are a type of collision in which both the total kinetic energy and momentum are conserved. The video script uses elastic collisions to illustrate the principles of conservation laws, showing that in such collisions, the kinetic energy remains the same before and after the collision, with a focus on rotational kinetic energy (\(\frac{1}{2} I \omega^2\)).

💡Inelastic Collisions

Inelastic collisions are collisions in which kinetic energy is not conserved, and some energy is transformed into other forms, such as heat or sound. The video explains that in inelastic collisions, the total kinetic energy decreases after the collision, and objects may move apart or stick together, with a special case being perfectly inelastic collisions where objects stick together after the collision.

💡Conservation Laws

Conservation laws state that certain quantities, like momentum and energy, remain constant in isolated systems. The video script frequently refers to conservation laws, particularly the conservation of angular momentum and linear momentum, to explain the behavior of objects in various scenarios, such as collisions and rotations.

💡Frictionless

The term 'frictionless' in the video script is used to describe conditions where there are no external forces or torques acting on a system. This is important for the conservation of linear and angular momentum, as it ensures that these quantities remain constant in the absence of friction.

💡Rotational Kinetic Energy

Rotational kinetic energy is the energy an object possesses due to its rotation. It is calculated as half the product of the object's moment of inertia and the square of its angular velocity (\(\frac{1}{2} I \omega^2\)). The video script discusses how this energy is a key factor in the analysis of rotational motion and collisions.

💡Cross Product

The cross product is a mathematical operation that takes two vectors and returns a third vector that is perpendicular to the plane containing the initial vectors. In the context of the video, the cross product is used to calculate the angular momentum of an object moving in a straight line, where it represents the vector product of the position vector and the linear momentum vector.

Highlights

Introduction to the concept of angular momentum and its conservation under certain conditions.

Explanation of how to calculate angular momentum for both rotating and straight-line moving objects.

Clarification that angular momentum is a vector quantity, unlike rotational inertia which is scalar.

The cross product relationship between position vector, velocity, and angular momentum for straight-line motion.

Importance of the perpendicular distance from the origin to the velocity vector in calculating angular momentum.

Connection between the conservation of linear momentum and the absence of external forces.

Analogous principle for the conservation of angular momentum related to the sum of torques.

Differentiation between elastic and inelastic collisions with respect to kinetic energy and rotational inertia.

Detailed walkthrough of a physics problem involving a rod, a ball, and conservation of angular momentum.

Application of conservation principles to solve for the velocity of a ball post-collision in a frictionless environment.

Calculation of the ratio of masses in an elastic collision scenario involving a rod and a ball.

Determination of the distance from the left ball to the center of mass after a collision in a rotational system.

Analysis of the change in kinetic energy as a result of a perfectly inelastic collision in a rotational system.

Solution for the angular speed of a disk after a student throws a rock tangentially on a frictionless platform.

Comparison of angular speeds in different scenarios involving a student on a rotating platform with and without a rock.

Final summary emphasizing the importance of understanding angular momentum, its conservation, and its application in physics problems.

Transcripts

Browse More Related Video

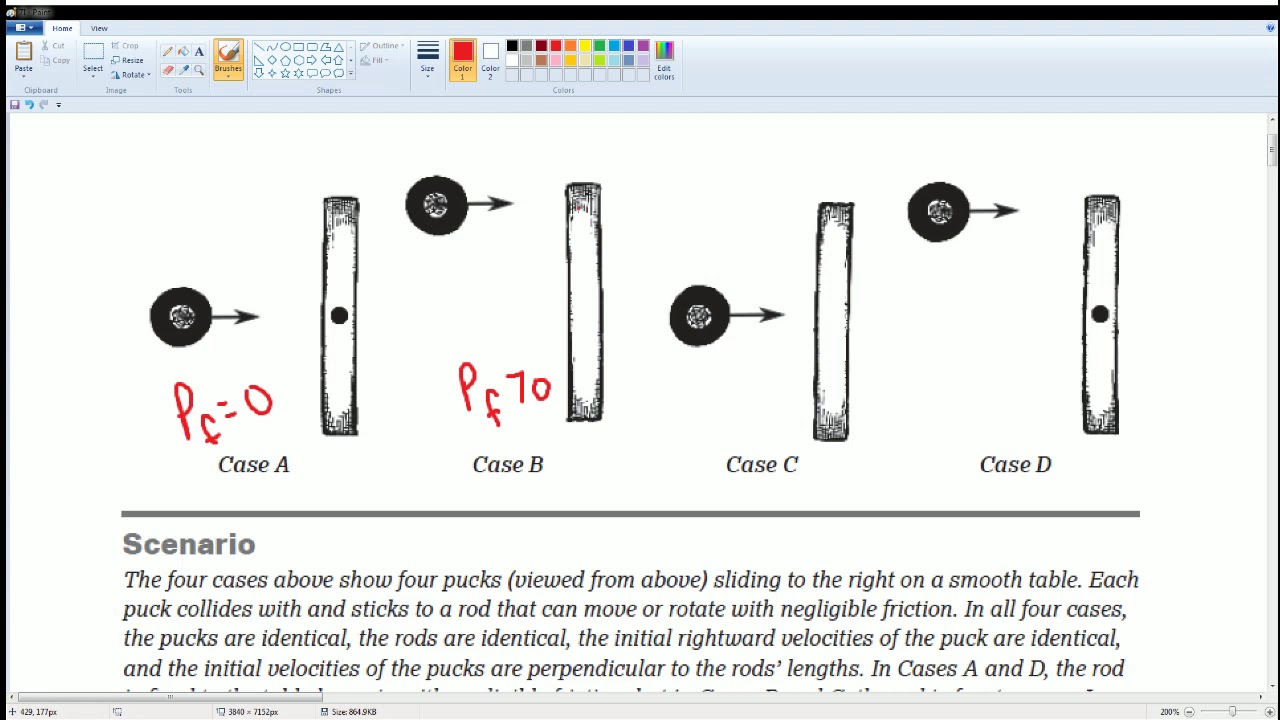
AP Physics Workbook 7.I Collisions "Old and Lack Full Explanation"

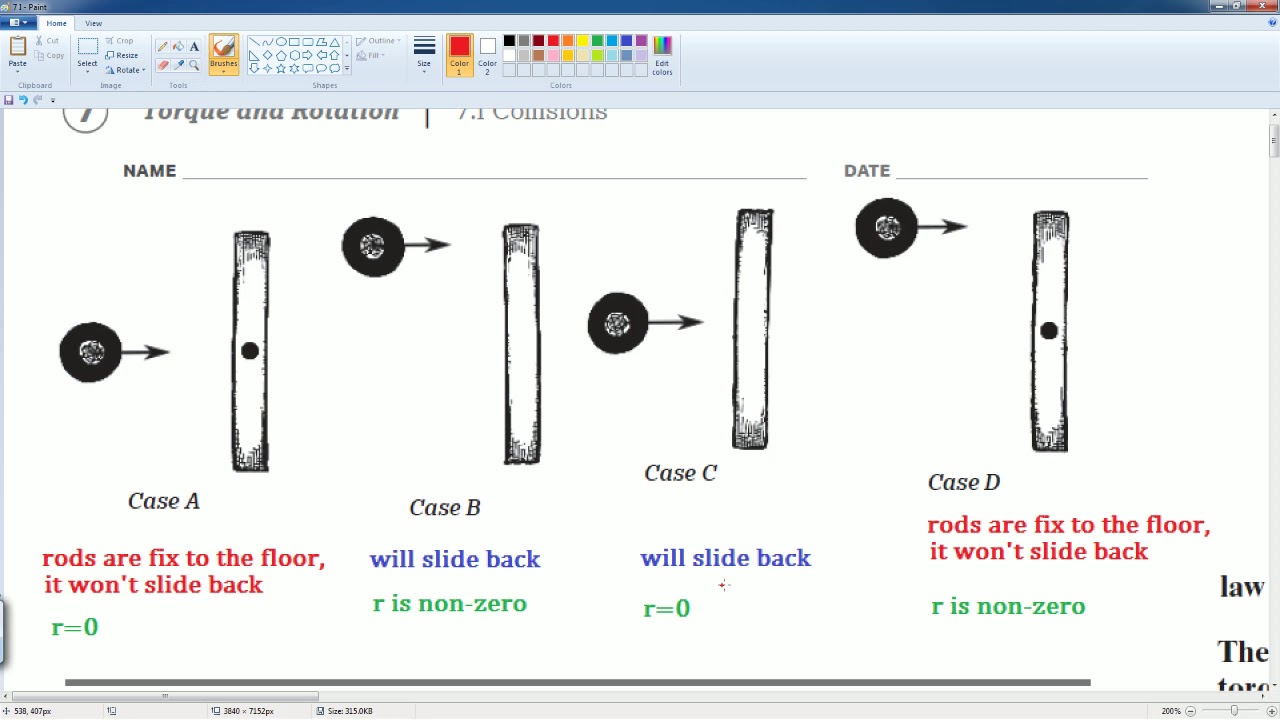
AP Physics Workbook 7.I Collisions "Updated and Fixed"

2022 Live Review 6 | AP Physics C: Mechanics | Rotational Dynamics and Angular Momentum

2022 Live Review 4 | AP Physics C: Mechanics | System of Particles and Linear Momentum

Differentiating Between Elastic and Inelastic Collisions | Physics in Motion

2021 Live Review 5 | AP Physics 1 | Impulse and Conservation of Momentum

Related Tags

Angular Momentum Rotational Inertia Physics C Mechanics Elastic Collisions Inelastic Collisions Conservation Laws Educational Review Physics Principles AP Daily Mechanics Tutorial