AP Physics Workbook 7.I Collisions "Old and Lack Full Explanation"
TLDRThis video script from the AP Physics workbook delves into the concepts of torque, rotation, and conservation of angular and linear momentum within collisions. It explains how angular momentum is defined and its relationship with the moment of inertia and angular velocity. The script uses a scenario involving a puck hitting various objects to illustrate the conservation laws and the changes in momentum and energy during collisions. It also discusses the difference between perfectly inelastic and elastic collisions, and how these affect momentum and kinetic energy. The video guides the viewer through determining which scenarios have constant or changing angular and linear momentum, and concludes with an example of a skater's spin to reinforce the concept of angular momentum.
Takeaways
- 📚 The session covers Unit 7 on Torque and Rotation, focusing on collision scenarios.
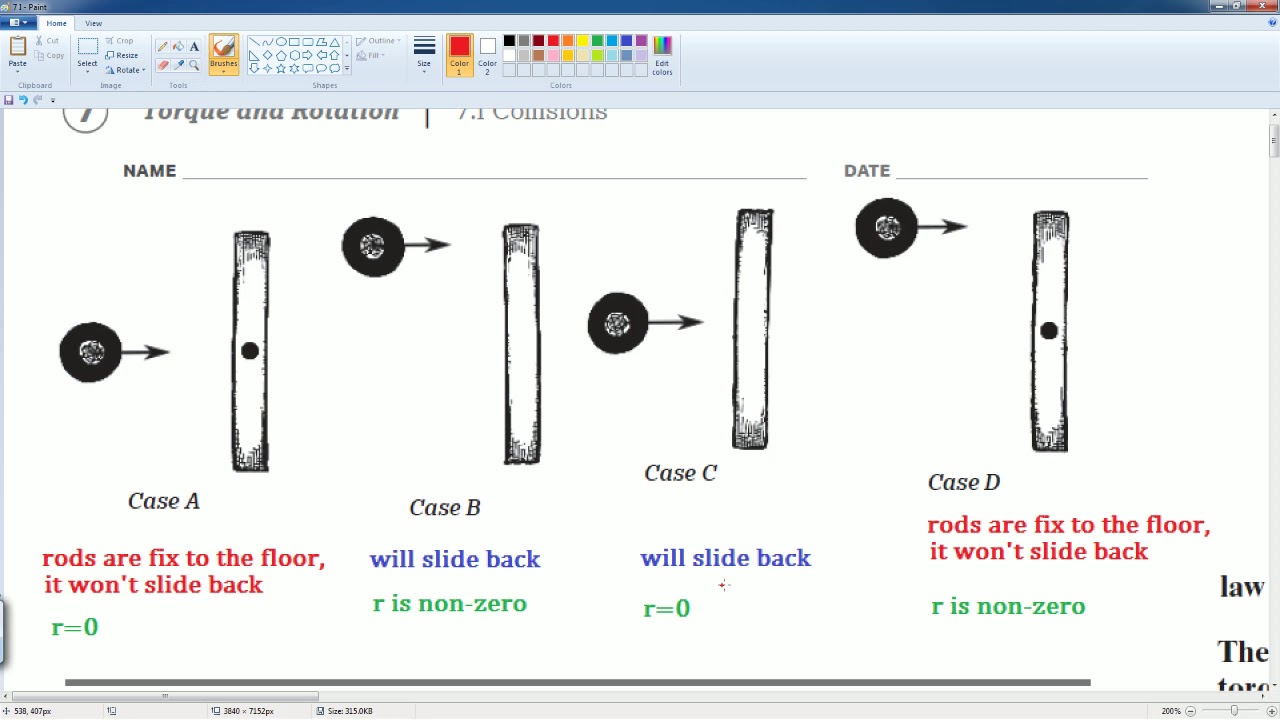
- 🏒 Part A involves a stick pinned down that can rotate freely when hit by a puck.
- 🔄 Angular momentum is defined as the product of the moment of inertia and angular velocity (L = I * ω).
- 💥 The law of conservation of angular momentum states that the total angular momentum remains constant if the net torque is zero.
- 🚫 Linear momentum and kinetic energy change during a collision, unless it's a perfectly inelastic or elastic collision.
- 📈 For scenario B and C, the puck hits at the top of the stick, leading to a perfectly inelastic collision and no loss of linear momentum.
- 🔄 In Part D, the puck hits a distance away from the axis of rotation, causing the stick to rotate and thus losing some but not all linear momentum.
- 🥊 The ranking of scenarios based on rightward linear momentum places A or D with the least and B and C with the most.
- 🎭 The concept of perfectly inelastic collision is explained, where the objects stick together and share the same final velocity.
- 🧍 The example of a skater spinning and the effect of changing the moment of inertia by bringing arms in is used to illustrate the conservation of angular momentum.
- 🔄 For the most clockwise angular momentum, B and D are identified as having the most due to the force being applied away from the center of rotation.
- 📊 The explanation for the ranking of scenarios based on clockwise angular momentum is provided, emphasizing the impact of the collision point relative to the axis of rotation.
Q & A
What is the main topic of the session in the transcript?
-The main topic of the session is Torque and Rotation in the context of collisions, as part of the AP Physics workbook, specifically focusing on the conservation of angular momentum, linear momentum, and kinetic energy.
What are the three physical quantities discussed in the scenario?
-The three physical quantities discussed are angular momentum, linear momentum, and kinetic energy.
How is angular momentum defined?
-Angular momentum is defined as the product of the moment of inertia (I) and angular velocity (ω), represented as L = I * ω.
What is the law of conservation of angular momentum for a rotating object?
-The law of conservation of angular momentum states that the total angular momentum of a rotating object remains constant if the net torque acting on it is zero.
How does the video script illustrate the conservation of linear momentum?
-The script illustrates that linear momentum is conserved when it's either a perfectly inelastic collision (when objects stick together) or an elastic collision (when there is an exchange of momentum and kinetic energy).
What happens to the puck in scenario A when it hits the stick?
-In scenario A, the puck hits the stick which is pinned down, preventing it from moving. The puck has no linear momentum after the collision due to the pinned condition.
Which scenario results in the least rightward linear momentum?
-Scenario A results in the least rightward linear momentum because the puck has no linear momentum after the collision as it is pinned down.
Which scenario has the most rightward linear momentum?
-Scenarios B and C have the most rightward linear momentum because they undergo a perfectly inelastic collision, retaining all linear momentum.
How does the video script explain the concept of a perfectly inelastic collision?
-A perfectly inelastic collision is when two objects stick together after the collision, resulting in the same final velocity for both objects. This type of collision conserves linear momentum but not kinetic energy.
What is the example given in the script to explain the conservation of angular momentum in a real-world scenario?
-The example given is that of a skater spinning on ice. When the skater brings their arms in closer to their body, they decrease their moment of inertia (I), which in turn increases their angular velocity (ω) to conserve angular momentum.
How does the script explain the ranking of scenarios based on the most clockwise angular momentum?
-The script explains that scenarios B and D have the most clockwise angular momentum because the puck hits the stick at a distance (R) from the center of rotation, creating a net torque and thus more angular momentum in the clockwise direction.
Outlines
📚 Introduction to Torque and Angular Momentum
This paragraph introduces the concepts of torque, rotation, angular momentum, linear momentum, and conservation of energy in the context of a physics problem involving a puck hitting various objects. The main focus is on understanding the conservation of angular momentum for a rotating object, which states that the total angular momentum remains constant if the net torque acting on it is zero. It also reviews the conservation of linear momentum and kinetic energy, emphasizing the difference between elastic and inelastic collisions. The paragraph sets the stage for analyzing specific scenarios based on these principles.
💡 Analysis of Collision Scenarios
This paragraph delves into the analysis of different collision scenarios between a puck and various objects, including a stick pinned down and a rod fixed to a table. The discussion revolves around determining whether angular momentum, linear momentum, and kinetic energy remain constant during these collisions. It highlights the importance of understanding the initial and final states of the objects involved and how the collisions affect their momentum and energy. The paragraph also introduces the ranking of scenarios based on the conservation laws and the outcomes of the collisions.
🔄 Ranking Scenarios Based on Angular Momentum
This paragraph focuses on ranking the collision scenarios based on the amount of clockwise angular momentum each scenario produces. It explains the relationship between the force applied, the distance from the center of rotation (torque), and the resulting angular momentum. The analysis includes a detailed examination of how the position of the collision (at the center or away from the center) affects the torque and, consequently, the angular momentum. The paragraph emphasizes the importance of visualizing and calculating the torque and angular momentum for each scenario to determine the ranking accurately.
Mindmap
Keywords
💡Torque
💡Angular Momentum
💡Linear Momentum
💡Collision
💡Kinetic Energy
💡Conservation Laws
💡Moment of Inertia
💡Elastic Collision
💡Perfectly Inelastic Collision
💡Rotational Motion
💡Workbook
Highlights
Discussion of angular momentum, linear momentum, and kinetic energy in the context of collisions and rotation.
Explanation of angular momentum as the product of moment of inertia and angular velocity.
Conservation of angular momentum for a rotating object when net torque is zero.
Momentum conservation in perfectly inelastic and elastic collisions.
Determination of whether angular momentum, linear momentum, and kinetic energy remain constant in different scenarios.
Explanation of how linear momentum changes during a collision.
Kinetic energy conservation in elastic collisions and its absence in inelastic ones.
Ranking of collision scenarios based on the conservation or change of physical quantities.
Analysis of puck's collision with objects causing changes in linear and angular momentum.
Explanation of perfectly inelastic collision where objects stick together and share the same final velocity.
Demonstration of how the distance from the axis of rotation affects the torque and angular momentum.
Comparison of angular momentum in scenarios where the puck hits at the center versus away from the center of rotation.
Practical example of a skater spinning and the effect of changing the moment of inertia on angular velocity.
Illustration of how the conservation of angular momentum causes a skater to speed up when bringing arms in.
Ranking of collision scenarios based on the amount of clockwise angular momentum generated.
Detailed explanation of why certain scenarios result in the least or most clockwise angular momentum.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: