AP Physics Workbook 7.I Collisions "Updated and Fixed"

Mr.S ClassRoom
7 Dec 202013:03
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial delves into the concepts of torque and rotation as covered in Unit 7 of the AP Physics workbook, specifically focusing on collisions. It explains the conservation of angular and linear momentum in various collision scenarios, emphasizing that angular momentum is conserved in all cases but linear momentum is not in cases where the object does not slide back. Kinetic energy conservation is only present in elastic collisions. The video also ranks the collisions based on the conservation of linear and angular momentum, using principles of torque and force to determine the outcomes.

Takeaways
  • 📚 The tutorial covers Unit Seven on Torque and Rotation in Physics, focusing on collisions.
  • 🔍 Scenario analysis is crucial for understanding the conservation of angular and linear momentum in different collision cases.
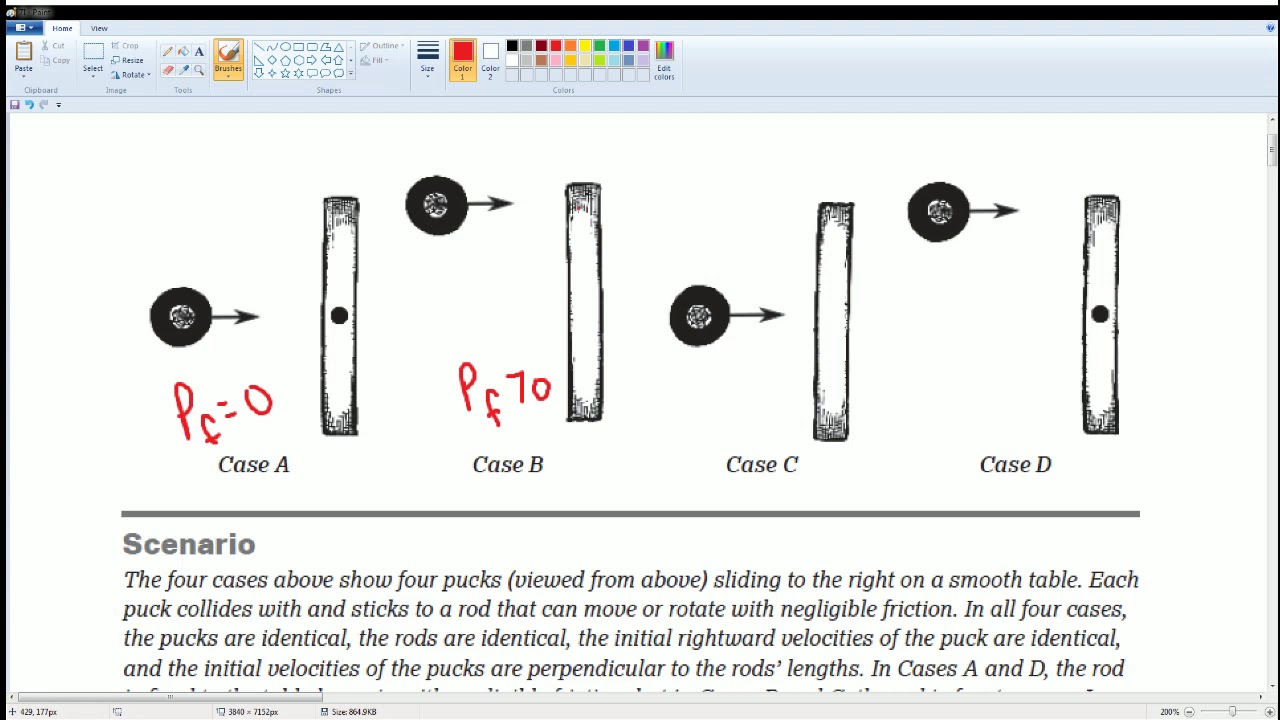
  • 🧱 Case A: The rod is fixed to the floor, hence no sliding back and r (the distance from the center of rotation) is zero.
  • 🏂 Case B: The rod slides back after the collision since r is non-zero, as the collision occurs away from the center.
  • 🚪 Case D: Similar to Case A, the rod is fixed and hits at a corner, making r non-zero, but no sliding back occurs.
  • 🔄 Conservation of angular momentum is discussed, stating that the initial angular momentum equals the final angular momentum, allowing the object to spin freely.
  • 💥 Types of collisions are categorized into perfectly inelastic, inelastic, and elastic, with momentum being conserved in all but kinetic energy only in elastic collisions.
  • ✅ All cases (A, B, C, and D) are conservative for angular momentum because they all spin and rotate.
  • 🚫 Linear momentum is not conserved in cases A and D because the rods are fixed and do not slide back, but it is conserved in B and C.
  • 🌟 Kinetic energy is not conserved in any scenario as the puck sticks to the rod after collision, resulting in perfectly inelastic collisions.
  • 📈 Ranking collisions based on linear momentum shows that B and C have the most, while A and D have less, with A being less than D.
  • 🔄 For angular momentum ranking, A equals C and B equals D, with the difference arising from the radius (r) values and the resulting torques.
Q & A

  • What is the main topic of the tutorial?

    -The main topic of the tutorial is torque and rotation in the context of collisions, specifically focusing on unit seven of the AP Physics workbook.

  • What are the two cases where the rod is fixed to the floor?

    -The two cases where the rod is fixed to the floor are case A and case D. In both cases, the rod won't slide back, and the collision is akin to hitting a wall.

  • How does the distance 'r' affect the conservation of angular momentum?

    -The distance 'r' is crucial for the conservation of angular momentum because it represents the radius from the center of rotation to the point of collision. Angular momentum is conserved when the initial and final angular momenta are equal, and 'r' plays a significant role in determining these values.

  • What is the law of conservation of angular momentum?

    -The law of conservation of angular momentum states that the initial angular momentum of a system is equal to the final angular momentum, provided the object is allowed to spin freely and the angular velocity is transferred during the collision.

  • In which type of collision is kinetic energy conserved?

    -Kinetic energy is conserved in an elastic collision. In perfectly inelastic and inelastic collisions, the total energy of the system decreases as some kinetic energy is lost when the objects stick together.

  • Why is linear momentum not conserved in case A and D?

    -Linear momentum is not conserved in case A and D because the rods are fixed to the floor and do not slide back after the collision. This means that the velocity is not transferred from the puck to the rod, leading to a loss of linear momentum.

  • Which cases have linear momentum conservation?

    -Cases B and C have linear momentum conservation because the pucks collide with the rods and stick to them, causing the rods to slide back and transfer the momentum from the puck to the rod.

  • How does the scenario describe perfectly inelastic collisions?

    -The scenario describes perfectly inelastic collisions as instances where the puck sticks to the rod after the collision, resulting in a loss of kinetic energy and no conservation of this energy.

  • Based on the conservation of linear and angular momentum, how would you rank the collisions from least to most rightward linear momentum?

    -From least to most rightward linear momentum, the ranking is A < D < B = C. Case A has the least because the rod is fixed and does not transfer momentum. Case D has some loss due to the non-zero 'r' value causing rotation. Cases B and C have the most because they involve a perfectly inelastic collision with momentum transfer.

  • How does the radius 'r' influence the ranking of collisions based on angular momentum?

    -The ranking based on angular momentum is A = C < B = D. Cases A and C have 'r' equal to zero, resulting in no net torque and thus no angular momentum. Cases B and D have the same 'r' value, leading to the same torque and angular momentum due to the same distance from the axis of rotation and identical pucks.

Outlines
00:00
📚 Introduction to Torque and Rotation

This paragraph introduces the topic of the video, which is the physics workbook tutorial covering unit seven on torque and rotation. It explains a scenario with three cases (A, B, and D) where a puck collides with a rod in different conditions. The focus is on understanding whether the collisions are conservative in terms of angular and linear momentum. The paragraph emphasizes the law of conservation of angular momentum and how it applies to the given scenarios. It also discusses the types of collisions (perfectly inelastic, elastic, and inelastic) and their relation to the conservation of momentum and kinetic energy.

05:03
🌪️ Analysis of Collision Types and Conservation Laws

This paragraph delves deeper into the analysis of the collisions mentioned in the previous section. It discusses the conservation of linear and angular momentum in cases A, B, and C, and explains why case D is different. The paragraph clarifies that while all cases have conservative angular momentum due to spinning, only cases B and C have conservative linear momentum because they slide back after the collision. Kinetic energy is not conserved in any of the cases due to the perfectly inelastic nature of the collisions where the puck sticks to the rod. The paragraph also ranks the collisions based on the conservation of linear momentum, concluding that cases B and C have the most rightward linear momentum.

10:03
🔄 Ranking Collisions based on Angular Momentum

The final paragraph focuses on ranking the collisions based on angular momentum. It uses the relationship between torque, force, and radius to explain why cases A and C have the same angular momentum, and why cases B and D also have the same but less than A and C. The explanation is based on the location of the collision relative to the axis of rotation and the resulting torque. The paragraph concludes by stating that cases B and D have the most clockwise angular momentum due to the same radius and force applied during the collision, while cases A and C have zero angular momentum because the collisions occur at the axis of rotation where the radius is zero.

Mindmap
Keywords
💡Torque
Torque is a measure of the rotational force acting on an object. In the context of the video, it is crucial for understanding how the collisions in the scenarios affect the rotation of the rod. For example, when the puck hits the rod at a point away from the center (non-zero r), it creates a torque that causes the rod to rotate.
💡Rotation
Rotation refers to the circular motion of an object around a fixed axis. In the video, the concept of rotation is central to understanding how the rod reacts after being hit by the puck in different scenarios. The rotation is directly related to the torque applied and the conservation of angular momentum.
💡Conservative
In the context of the video, conservative refers to whether certain quantities, like angular momentum or kinetic energy, remain constant before and after the collision. A conservative system is one where these quantities do not change due to external influences.
💡Angular Momentum
Angular momentum is a measure of the rotational motion of an object. It is a vector quantity that depends on the object's moment of inertia, angular velocity, and the direction of rotation. In the video, the conservation of angular momentum is a key principle used to analyze the scenarios presented.
💡Collision
A collision is a short-lived interaction between two or more bodies that results in a change in their motion. In the video, different types of collisions (elastic, inelastic, and perfectly inelastic) are discussed to understand how they affect the conservation of momentum and energy.
💡Linear Momentum
Linear momentum is the product of an object's mass and its velocity. It describes the motion of an object along a straight path. In the video, the conservation of linear momentum is discussed in relation to whether the rod slides back after the collision or not.
💡Kinetic Energy
Kinetic energy is the energy an object possesses due to its motion. It is directly proportional to the mass of the object and the square of its velocity. In the video, the conservation of kinetic energy is discussed in the context of perfectly inelastic collisions, where the kinetic energy is not conserved because the objects stick together after the collision.
💡Perfectly Inelastic Collision
A perfectly inelastic collision is a type of collision where the two objects stick together and move as one after the collision. In such collisions, kinetic energy is not conserved because some of it is converted into other forms of energy, like heat or deformation.
💡Radius (r)
The radius (r) in the context of the video refers to the distance from the point of collision to the axis of rotation. The value of r is crucial in determining the torque and, consequently, the angular momentum of the system after the collision.
💡Work
Work in physics is defined as the product of the force applied to an object and the displacement of the object in the direction of the force. It is a measure of energy transfer. In the video, the concept of work is implicitly discussed when analyzing the transfer of energy during collisions.
💡Force
Force is any action that causes an object to accelerate or change its motion. In the video, the force is applied by the puck when it collides with the rod, which can result in linear and/or angular motion depending on the conditions of the collision.
Highlights

The tutorial covers unit seven on torque and rotation, focusing on collision scenarios.

In case A, the rod is fixed to the floor and won't slide back, with the distance of collision (r) being zero.

Case B involves a rod that slides back with a non-zero collision distance (r) since it hits at a corner away from the center.

Case D is similar to hitting a wall, with the rod fixed to the ground and hitting at a corner, resulting in a non-zero collision distance (r).

Angular momentum is conserved when the initial equals the final, allowing the object to spin freely.

All three types of collisions (perfectly inelastic, elastic, and inelastic) conserve momentum, but only elastic collisions conserve kinetic energy.

Cases A, B, and C all have conservative angular momentum because they are allowed to spin and rotate.

Linear momentum is only conserved in cases B and C, as A and D do not slide back after the collision.

Kinetic energy is not conserved in any scenario because the puck sticks to the rod after the collision, resulting in perfectly inelastic collisions.

Cases B and C have the most rightward linear momentum due to the puck's velocity being transferred to the rod.

Case A has the least linear momentum because the rod is fixed to the floor and does not move.

Case D loses some but not all linear momentum due to the collision occurring at a distance from the axis of rotation.

Angular momentum can be seen as torque times delta t, and torque can also be seen as the radius times the force.

Cases A and C have no net torque created due to the collision occurring at the axis of rotation, resulting in zero angular momentum.

Cases B and D have the same amount of clockwise angular momentum due to the same radius and force applied.

The tutorial provides a comprehensive understanding of the conservation of angular and linear momentum in various collision scenarios.

Transcripts

Browse More Related Video

AP Physics Workbook 7.I Collisions "Old and Lack Full Explanation"

Conservation of Linear Momentum

Elastic and Inelastic Collisions

AP Physics 1 Momentum Review

2021 Live Review 7 | AP Physics C: Mechanics | Angular Momentum & Rotational Collisions

2022 Live Review 6 | AP Physics C: Mechanics | Rotational Dynamics and Angular Momentum

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsTorque AnalysisRotation DynamicsCollision TypesMomentum ConservationKinetic EnergyElastic CollisionsPerfectly InelasticAngular MomentumPhysics Tutorial