2021 Live Review 5 | AP Physics 1 | Impulse and Conservation of Momentum
TLDRIn this engaging AP Physics lecture, Christine Gonzalez Vega delves into the concept of momentum, exploring its conservation and relationship with collisions. Through various examples and diagrams, she explains how momentum, a vector quantity, remains constant in the absence of net external forces, particularly during collisions. The lecture also touches on the conservation of energy, differentiating between elastic, inelastic, and totally inelastic collisions, and how these principles apply to real-world scenarios. Gonzalez Vega employs interactive elements, such as polls and practice problems, to reinforce the concepts and encourage active learning.
Takeaways
- 🌟 Momentum is a vector quantity, meaning both magnitude and direction are important.
- 📈 The conservation of momentum applies when there are no net external forces acting on a system, typically during collisions.
- 🔄 Impulse is the change in momentum, calculated as the force applied times the time interval it is applied.
- 💥 In an elastic collision, both momentum and energy are conserved, whereas in inelastic and totally inelastic collisions, energy is not conserved.
- 📊 Force-time graphs can be used to determine changes in momentum; the area under the graph represents the impulse.
- 🚀 When analyzing collisions, it's crucial to consider the masses of the objects involved and how they affect the final velocities post-collision.
- 🎯 Practice problems and diagrams help solidify understanding of momentum conservation and the effects of different types of collisions.
- 🔄 For two-dimensional collisions, momentum conservation must be considered separately for the x and y components.
- 📌 In a system with a spring, the potential energy stored in the spring is converted to kinetic energy when the spring is released.
- 🤔 When solving problems, always consider the initial and final states of the system and apply the conservation laws accordingly.
- 🔍 It's essential to draw free body diagrams, momentum bar charts, or lollapalooza charts to visualize and organize the physics concepts involved.
Q & A
What is the definition of momentum?
-Momentum is a vector quantity that represents the mass of an object in motion. It is calculated as the product of an object's mass and its velocity.
How does momentum relate to Newton's second law?
-Momentum is directly related to Newton's second law, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration (F = ma). If we rearrange this equation to solve for the force (F = Δp / Δt), we can see that the force applied over a time interval (impulse) is equal to the change in momentum, reinforcing Newton's second law.
What is the difference between a paper-pencil version and a digital version of the AP Physics exam?
-The paper-pencil version of the AP Physics exam consists of two sections, each 90 minutes long, with a multiple-choice section of 50 questions and a free-response section with five questions. The digital version has a similar structure, but the second section includes 25 additional multiple-choice questions and two free-response questions, one of which is a paragraph-length response.
How can you determine if a collision is elastic or inelastic?
-An elastic collision is one where the objects bounce off each other and the system's energy is conserved. In an inelastic collision, the objects also bounce off but energy is not conserved due to some form of deformation or work done during the collision. A totally inelastic collision is when the objects stick together and come to a stop, often involving significant energy loss.
What is the significance of the impulse-momentum theorem?
-The impulse-momentum theorem is significant because it states that the change in an object's momentum is equal to the impulse applied to it. This relationship is crucial for understanding and calculating the effects of forces on objects over time intervals, especially in collisions and other interactions.
How can you use a force-time graph to find the impulse?
-In a force-time graph, the area under the curve represents the impulse. This area can be calculated as half the product of the force and the time interval (Impulse = 1/2 * Force * Time). The slope of the graph (force divided by time) also gives you the rate of change of momentum per unit time.
What is the role of friction in the conservation of momentum?
-Friction is a force that can act on the system during a collision or interaction, leading to a change in momentum. It is considered an external force when it is not balanced by an equal and opposite force within the system, and it can cause a loss of momentum and a transfer of energy from the system in the form of heat.
How does the mass of an object affect its momentum?
-The mass of an object directly affects its momentum. For a given velocity, an object with a greater mass will have a greater momentum. This is because momentum is calculated as the product of mass and velocity (p = mv). Therefore, heavier objects moving at the same speed will have more momentum than lighter objects.
What is the conservation of momentum principle?
-The conservation of momentum principle states that the total momentum of a closed system of objects remains constant if no external forces act on the system. This means that the sum of the individual momenta of all objects within the system before an interaction or collision must equal the sum of the individual momenta after the interaction or collision.
How can you predict the outcome of a collision using momentum conservation?
-By applying the conservation of momentum principle, you can predict the outcome of a collision by calculating the total initial momentum of the system and equating it to the total final momentum. This allows you to determine the velocities and directions of the objects after the collision, assuming no external forces are acting on the system.
What is the relationship between momentum and energy in collisions?
-While momentum and energy are related, they are not the same. Momentum is a vector quantity that considers both mass and velocity, while energy is a scalar quantity. In an elastic collision, both momentum and kinetic energy are conserved. However, in an inelastic or totally inelastic collision, kinetic energy is not conserved and is often transformed into other forms of energy, such as heat or potential energy due to deformation.
Outlines
🌟 Introduction to Momentum and Collisions
The video begins with an introduction to the concept of momentum and the plan to discuss various aspects of it, including impulse, conservation of momentum, and collisions. The host, Christine Gonzalez Vega, welcomes viewers to AP Physics One and addresses feedback from previous sessions. She provides information about the AP exam, directing viewers to the College Board's AP Central for updates and resources. The video aims to cover the basics of momentum, its conservation, and the role of energy in collisions, using equations, graphs, and real-life examples to illustrate the concepts.
📚 Equations and Graphs for Momentum
This paragraph delves into the equations related to momentum, such as the definition of momentum (mass times velocity) and the concept of impulse (force times time). It explains how these relate to Newton's second law and how to use them to solve problems involving changes in velocity. The video also introduces different types of graphs that can represent momentum and force, such as force-time graphs and position-time graphs. The host emphasizes the importance of understanding these graphical representations for predicting and analyzing momentum-related scenarios, especially in the context of collisions.
🎓 System Analysis and Impulse-Momentum Graphs
The host continues the discussion on momentum by explaining how to analyze a system in terms of momentum conservation. It covers the distinction between internal and external forces and how they affect the momentum of a system. The concept of impulse-momentum graphs is introduced as a tool for visualizing and solving problems. These graphs help to organize the interactions between objects and external forces, allowing for a better understanding of changes in momentum. The video provides an example using a pendulum and a box to demonstrate how to apply these concepts.
🚗 Collisions and Momentum Conservation
This section focuses on the application of momentum conservation in collisions. The host distinguishes between different types of collisions, such as elastic, inelastic, and totally inelastic collisions, and how they relate to energy conservation. The video uses examples of carts colliding to illustrate the principles of momentum transfer and conservation. It also discusses the prediction of velocities and directions of moving objects after collisions using the conservation of momentum principle. The host encourages viewers to practice sketching momentum graphs and solving related problems.
🔄 Two-Dimensional Collisions and Center of Mass
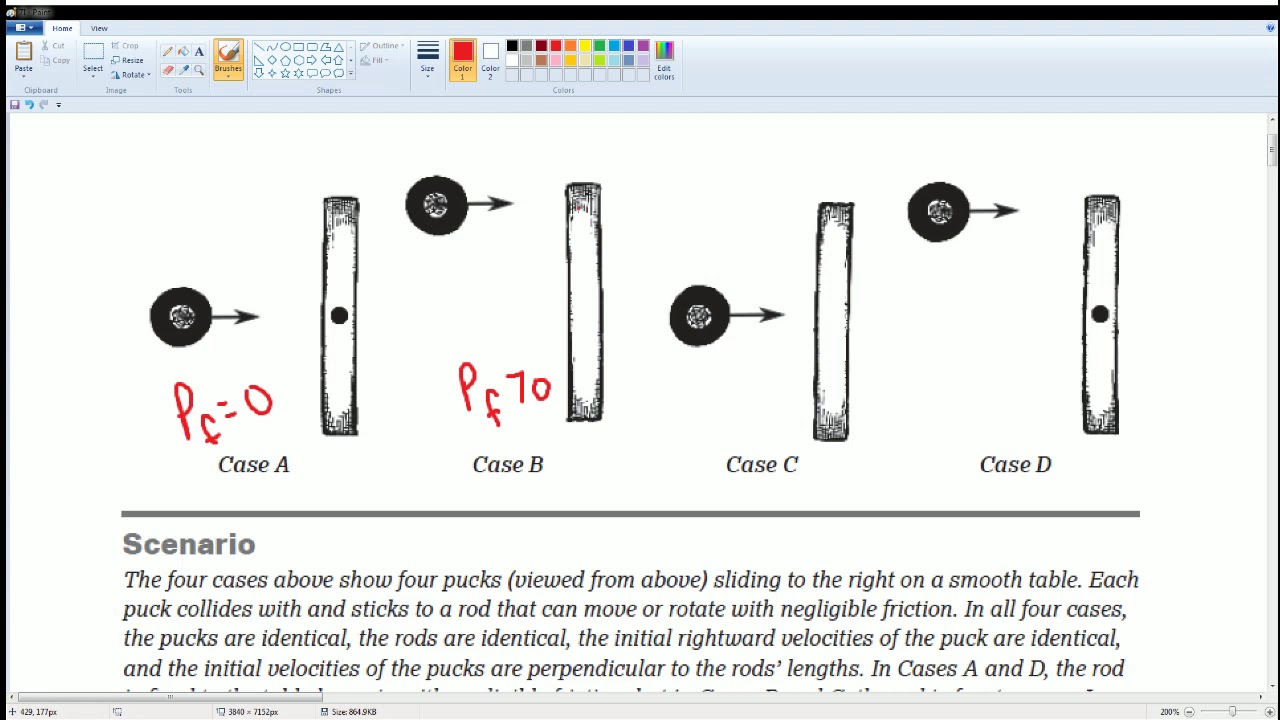
The video explores collisions in two dimensions, emphasizing that momentum is a vector quantity and must be conserved separately along each axis. The host uses the example of pucks colliding to demonstrate how to analyze and predict the outcomes of such collisions. The concept of the center of mass is introduced, and its role in the motion of objects is discussed, particularly in the context of rotating objects resulting from off-center collisions. The video also touches on the use of Velcro to simulate totally inelastic collisions and how this affects the center of mass and momentum conservation.
📊 Practice Problems and Spring Collisions
The host presents practice problems to reinforce the concepts learned about momentum and collisions. These problems involve analyzing the linear momentum and kinetic energy of carts with a spring between them, from the moment they are released to when the spring returns to its natural length. The video explains why momentum is conserved in these scenarios and how the potential energy stored in the spring is converted into kinetic energy. The host also addresses a specific problem involving two carts with different masses, their velocities, and the conservation of momentum upon collision.
📝 Summary and Additional Resources
In the concluding part, the host summarizes the main takeaways from the video, emphasizing the conservation of momentum in the absence of net external forces and the role of mass in determining velocities in collisions. The importance of elastic collisions in energy conservation is highlighted, as well as the loss of energy in inelastic and totally inelastic collisions. The host encourages viewers to continue practicing with diagrams and momentum charts. Additional resources, including links to previous videos and a feedback form, are provided for further learning and engagement.
Mindmap
Keywords
💡Conservation of Momentum
💡Impulse
💡Elastic Collision
💡Inelastic Collision
💡Totally Inelastic Collision
💡Center of Mass
💡Vector Quantity
💡Free Body Diagram
💡Kinetic Energy
💡Force-Time Graph
Highlights
Conservation of momentum is a fundamental concept in physics, demonstrated through various experiments and scenarios.
Momentum is a vector quantity, meaning it has both magnitude and direction, and is product of an object's mass and velocity.
Impulse is the change in momentum, calculated as the force applied over the time interval it was applied.
Collisions are a common scenario where momentum conservation is observed, especially in perfectly elastic collisions.
The total momentum of an isolated system remains constant when no external forces act upon it, a principle known as the conservation of momentum.
Energy conservation is another important principle, but unlike momentum, energy is not always conserved in collisions, especially in inelastic or non-elastic collisions.
In an elastic collision, both momentum and energy are conserved, whereas in an inelastic collision, only momentum is conserved.
Explosions represent a scenario where energy is added to a system, resulting in an increase in kinetic energy.
When analyzing collisions in two dimensions, it's crucial to consider the conservation of momentum in both the x and y directions separately.
The center of mass of a system provides a useful reference point for analyzing motion, especially in collisions and after impacts.
Practical applications of momentum and energy conservation can be seen in phenomena such as car crashes, billiard ball movements, and even everyday activities like playing pool.
In a totally inelastic collision, objects stick together and move as one, resulting in the transfer of momentum and a decrease in velocity.
Graphical representations, such as force-time graphs and momentum-bar charts, are powerful tools for visualizing and calculating changes in momentum.
The concept of momentum is not only essential for understanding physical phenomena but also for solving problems in mechanics and preparing for exams like the AP Physics 1.
Teaching methods like drawing free-body diagrams and using LL diagrams can greatly aid in conceptual understanding and problem-solving in physics.
The session also covered how to apply conservation laws in complex scenarios, such as systems with varying masses, spring interactions, and collisions with non-zero initial momentum.
The importance of practice and application of these principles was emphasized, with several examples and exercises provided for better understanding.
Transcripts
Browse More Related Video
AP Physics Workbook 7.I Collisions "Old and Lack Full Explanation"

AP Physics 1 review of Momentum and Impulse | Physics | Khan Academy

AP Physics 1 Momentum Review

2021 Live Review 7 | AP Physics C: Mechanics | Angular Momentum & Rotational Collisions

8. Dynamics of Multiple-Body System and Law of

2021 Live Review 4 | AP Physics 1 | Understanding Work and Energy
5.0 / 5 (0 votes)
Thanks for rating: