How to read F Distribution Table used in Analysis of Variance (ANOVA)
TLDRThis tutorial video offers a step-by-step guide on reading and interpreting F-distribution tables, essential for statistical analysis. The F-ratio, calculated from an ANOVA test, is compared with critical values from the table to determine the rejection or acceptance of the null hypothesis. The video explains how to find critical values for different degrees of freedom and significance levels, highlighting the process with visual aids. It also encourages viewers to explore further with a dedicated playlist on ANOVA.
Takeaways
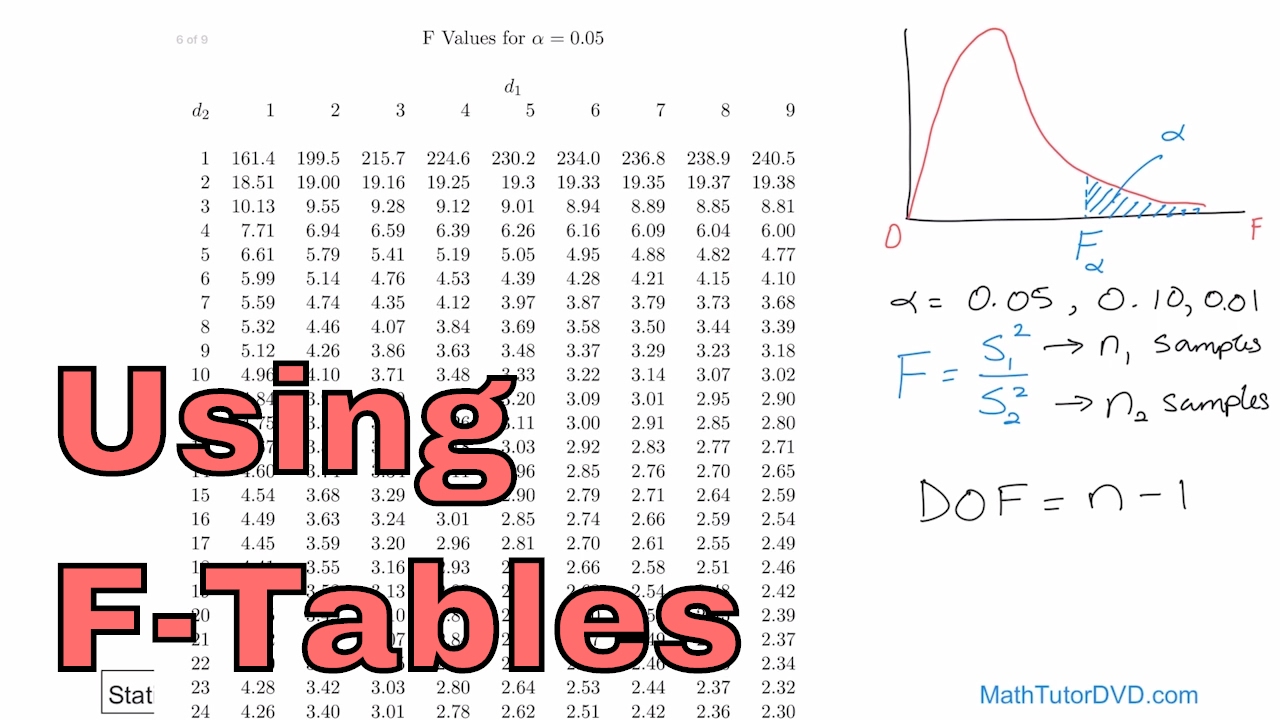
- 📚 The tutorial explains how to read F-distribution tables found in statistics books.
- 📉 The F-distribution is depicted along the horizontal axis with the F-ratio and a non-bell curve shape.
- 🔍 The body of the table contains critical values which are used to determine the outcome of an F-test.
- ❌ If calculated values exceed the critical value, it falls in the rejection region, leading to the rejection of the null hypothesis.
- ✅ Conversely, if calculated values are less than the critical value, the null hypothesis is not rejected.
- 📏 The first value in the F-test represents the degrees of freedom of the numerator, related to the number of groups or samples.
- 📐 The second value is the degrees of freedom of the denominator, related to the total number of observations.
- 🔢 The table's top rows indicate the degrees of freedom for the numerator, and the vertical columns for the denominator.
- 🌐 Critical values are often presented with different levels of significance, such as 0.05 and 0.01.
- 📝 The tutorial demonstrates how to find a specific critical value by intersecting the degrees of freedom for the numerator and denominator.
- 📈 The critical value found in the example is 3.89, which helps visualize the F-ratio and its relation to the rejection region.
- 📚 The video series also covers how to calculate the analysis of variance (ANOVA) and encourages viewers to watch the playlist for more information.
Q & A
What is the main topic of the tutorial?
-The tutorial is about how to read and interpret F-distribution tables, which are used in statistical analysis, specifically in the context of an Analysis of Variance (ANOVA) test.
What are the two values that define the F-test in the context of the tutorial?
-The two values that define the F-test are the degrees of freedom of the numerator and the degrees of freedom of the denominator.
How is the horizontal axis of the F-distribution table labeled?
-The horizontal axis of the F-distribution table is labeled with the F ratio, which is calculated with the ANOVA test.
What does the shape of the F-distribution curve look like?
-The shape of the F-distribution curve is not exactly like a bell curve; it has a unique shape that is part of the F-distribution.
What are critical values in the context of the F-distribution table?
-Critical values are the values in the body of the F-distribution table that are used to determine the rejection region for a hypothesis test.
What does it mean if the calculated F ratio is greater than the critical value?
-If the calculated F ratio is greater than the critical value, it falls in the rejection region, leading to the rejection of the null hypothesis.
What is the significance of the degrees of freedom for the numerator and denominator in the F-distribution table?
-The degrees of freedom for the numerator relate to the number of groups or samples under study, while the degrees of freedom for the denominator relate to the total number of observations.
What is the level of significance typically denoted by 'α' in statistical tests?
-The level of significance denoted by 'α' (alpha) is the probability of rejecting the null hypothesis when it is true, often set at 0.05 or 0.01.
How are the critical values for different levels of significance represented in the F-distribution table?
-Critical values for different levels of significance, such as 0.05 and 0.01, are represented with different notations, with 0.05 often highlighted in red and 0.01 represented by bold values.
What should one do if their ANOVA test results are less than the critical value from the F-distribution table?
-If the ANOVA test results are less than the critical value, it means that the null hypothesis is not rejected, indicating that there is not enough evidence to support the alternative hypothesis.
What is the tutorial's advice regarding sharing knowledge and staying updated with new information?
-The tutorial encourages viewers to watch the playlist on ANOVA, share the knowledge on social media platforms like Facebook, Google+, and Twitter, and to subscribe to the channel for new information.
Outlines
📚 Understanding F-Distribution Tables in Statistics
This paragraph introduces a tutorial on how to read F-distribution tables found in statistics books. The speaker explains that these tables are essential for conducting an Analysis of Variance (ANOVA) test. They describe the structure of the table, which includes the F-ratio on the horizontal axis and critical values within the table body. The critical values are used to determine the rejection region for the null hypothesis. If the calculated F-value is greater than the critical value, the null hypothesis is rejected. The tutorial also explains the meaning of degrees of freedom for both the numerator and the denominator, which are crucial for locating the correct critical value in the table. The speaker illustrates the process with an example, showing how to find the critical value for a specific set of degrees of freedom and a significance level of 0.05.
🔍 Application of F-Test Results in Hypothesis Testing
In this paragraph, the speaker discusses the application of F-test results in the context of hypothesis testing. They provide an example scenario where the calculated F-value from an ANOVA test is compared to the critical value obtained from the F-distribution table. If the calculated F-value is less than the critical value, as in the example where the F-value is less than 3.89, the null hypothesis is not rejected. The speaker emphasizes the importance of understanding the relationship between the calculated F-value and the critical value for making correct inferences in statistical analysis. They also encourage viewers to watch a playlist on ANOVA for a deeper understanding and invite them to share, comment, and subscribe for more educational content.
Mindmap
Keywords
💡NOA tables
💡F-distribution tables
💡Analysis of Variance (ANOVA)
💡F-ratio
💡Critical values
💡Degrees of freedom
💡Null hypothesis
💡Rejection region
💡Level of significance
💡F-test
Highlights
Tutorial on how to read F-distribution tables found in statistics books.
Explanation of the F-ratio used in the analysis of variance test.
Description of the F-distribution curve's unique shape compared to a bell curve.
Importance of critical values in the F-distribution table for hypothesis testing.
How to determine the rejection region based on calculated values and critical values.
Guidance on rejecting the null hypothesis if calculated F ratio exceeds the critical value.
Instructions on failing to reject the null hypothesis if the F ratio is less than the critical value.
Details on degrees of freedom for the numerator and its relation to groups or samples.
Clarification on degrees of freedom for the denominator and its relation to total observations.
Identification of critical values in the F-distribution table for different significance levels.
Highlighting the presence of both 0.05 and 0.01 critical values in the table.
Demonstration of finding a specific critical value using degrees of freedom.
Visual representation of the F ratio and critical value on a curve.
Example calculation of an F test result and comparison with the critical value.
Implication of results greater than the critical value for hypothesis testing.
Scenario where F test results are less than the critical value leading to a failure to reject the null hypothesis.
Encouragement to watch a playlist on ANOVA for further understanding.
Invitation to share knowledge and engage with the content on social media platforms.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: