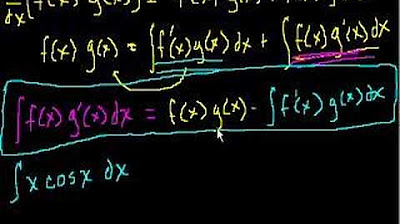Integration By Parts
TLDRThis educational video script introduces the concept of integration by parts, a technique used when integrating products of algebraic and transcendental functions. It explains the formula's derivation from the product rule of differentiation, and demonstrates its application through examples, including integrating x sine x and x squared e to the x. The script also covers a tabular method for integrating powers of x and concludes with handling limits in integration and a trick to break cycles in repeated integration by parts, encouraging practice for mastery.
Takeaways
- 📚 Integration by parts is a technique used when direct integration methods fail, especially for products of algebraic and transcendental functions.
- 🔄 The formula for integration by parts is derived from the product rule of differentiation, leading to the integral of uv being uv minus the integral of vdu.
- ✅ To apply integration by parts, select 'u' to be an easily differentiable function and 'dv' to be easily integrable.
- 📉 An example given is integrating x * sin(x), where x is chosen as 'u' and sin(x) as 'dv', resulting in a process that may require repeating integration by parts.
- 🔍 When integrating (x^2) * e^x, the process involves multiple steps of integration by parts, simplifying the integral into a manageable form.
- 📝 A tabular method is introduced for integrating powers of x with e^x, making the process systematic and less prone to error.
- 🔢 For definite integrals, integrate without limits first, then apply the limits to evaluate the result.
- 🔄 Even when faced with a cycle in integration by parts, such as with e^x * cos(x), algebraic manipulation can break the cycle and find a solution.
- ✳️ The script emphasizes the importance of practice in mastering the technique of integration by parts.
- 📈 The method of integration by parts is applicable to a variety of functions, including those without a clear 'x' term, by strategically choosing 'u' and 'dv'.
- 📚 The transcript concludes with an encouragement to practice integration by parts, highlighting its utility in calculus.
Q & A
What is integration by parts used for?
-Integration by parts is used when you can't integrate a function using other standard forms, typically when you have a product of two functions, such as an algebraic or polynomial function times a transcendental function.
How is the formula for integration by parts derived?
-The formula is derived from the product rule for derivatives. By integrating both sides of the product rule equation, you get the integral of u*dv = uv - the integral of v*du, which is rearranged to uv - ∫vdu = ∫u dv.
What should you consider when choosing 'u' and 'dv' for integration by parts?
-Choose 'u' as something easy to differentiate and 'dv' as something easy to integrate. It's often beneficial to let the trigonometric function be 'dv' and the exponential function be 'u'.
What is the integral of x*sin(x)dx using integration by parts?
-By setting u=x and dv=sin(x)dx, you find du=1dx and v=-cos(x). Applying the formula, the integral becomes -x*cos(x) + ∫cos(x)dx, which simplifies to -x*cos(x) + sin(x) + C.
Can you explain the process of solving the integral of x^2*e^x dx using integration by parts?
-First, set u=x^2 and dv=e^x dx, get du=2x dx and v=e^x. Apply the formula to get x^2*e^x - 2x*e^x. Then, you may need to apply integration by parts again to solve for the remaining integral, 2x*e^x dx.
What is the algebraic trick used to solve the integral of e^x*cos(x)dx without an infinite cycle?
-The trick is to recognize that the integral of e^x*cos(x)dx appears on both sides of the equation. By adding the integral to both sides and simplifying, you can solve for the integral without an infinite cycle.
How can you use a table to solve an integral with powers of x and e^x?
-Create a table with columns for 'u' and 'dv'. Fill in the derivatives of 'u' and the integrals of 'dv'. Multiply the top left by the diagonals and alternate signs to find the solution.
What happens when you have limits on the integral during integration by parts?
-Ignore the limits during the integration process. After finding the antiderivative, plug in the limits to evaluate the definite integral.
Why is it recommended to always let the trigonometric function be 'dv' when integrating by parts?
-Trigonometric functions are easier to integrate than their derivatives, which are typically simpler exponential functions. This choice simplifies the process and makes the integration by parts formula easier to apply.
Can you provide an example of a situation where integration by parts seems to lead to an infinite cycle?
-An example is the integral of e^x*cos(x)dx. It appears to lead to an infinite cycle because the integral of e^x*cos(x)dx keeps reappearing. However, using an algebraic trick can break this cycle.
What is the final answer for the integral of e^x*cos(x)dx after applying the algebraic trick?
-After applying the algebraic trick and simplifying, the final answer is (e^x/2) * (sin(x) + cos(x)) + C.
Outlines
📚 Introduction to Integration by Parts
This paragraph introduces the concept of integration by parts, a technique used when direct integration methods fail. It's particularly useful for integrating products of algebraic and transcendental functions. The explanation begins with the product rule for derivatives, which is then integrated to derive the formula for integration by parts. The formula is uv - ∫v du, where u and dv are chosen for ease of differentiation and integration, respectively. The paragraph provides an example of integrating x * sin(x), demonstrating how to apply the formula step by step.
🔁 Applying Integration by Parts with Repeated Process
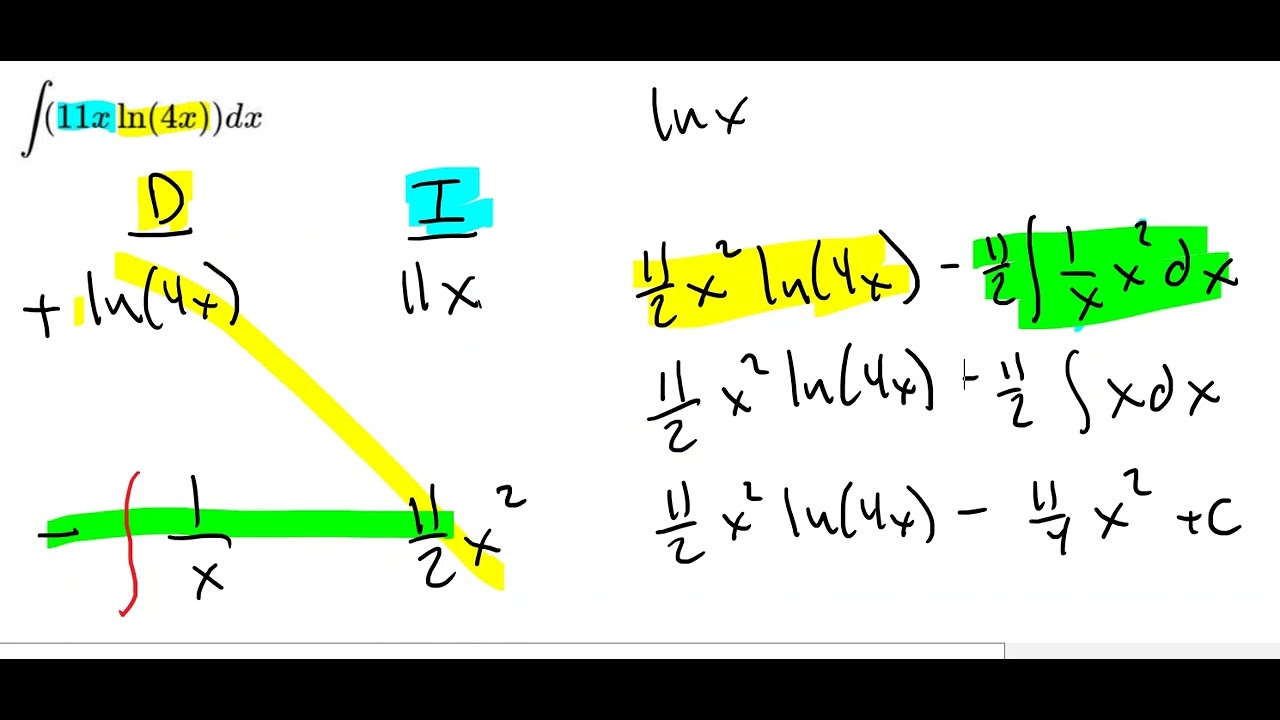
The second paragraph delves into a more complex example where integration by parts must be applied iteratively due to the nature of the integral. The example involves integrating x^2 * e^x, which requires setting up u and dv, taking derivatives, and integrating to find v. The process is repeated because the result still contains a product that requires integration by parts. The paragraph also introduces a tabular method for handling powers of x, which simplifies the process and leads to the same result as the iterative method.
📉 Integration by Parts with Limits
This paragraph discusses how to handle definite integrals using integration by parts. The example provided is the integral of x * sin(x) from 0 to π/2. The process involves first integrating without considering the limits and then substituting the limits into the indefinite integral to find the final result. The example demonstrates that the integral evaluates to 1 after applying the limits.
🔄 Dealing with Trigonometric and Exponential Functions
The final paragraph addresses a scenario where the integral involves transcendental functions without a clear power of x. The example given is the integral of e^x * cos(x). The paragraph illustrates the process of repeatedly applying integration by parts and then uses an algebraic trick to break the cycle of repeated integrations. By adding the integral of e^x * cos(x) to both sides of the equation and simplifying, the paragraph shows how to find the solution to such integrals without endless iteration.
Mindmap
Keywords
💡Integration by Parts
💡Algebraic Function
💡Transcendental Function
💡Product Rule
💡Derivative
💡Integral
💡u and dv
💡Trigonometric Function
💡Exponential Function
💡Definite Integral
💡Algebraic Manipulation
Highlights
Introduction to integration by parts, a method used when other integration forms are not applicable.
Integration by parts is typically used for products of algebraic or polynomial functions and transcendental functions.
Derivation of the integration by parts formula from the product rule of derivatives.
Integration by parts formula: ∫udv = uv - ∫vdu.
Example of integrating x sine x using integration by parts.
Explanation of choosing u and dv for integration by parts, emphasizing simplicity in derivatives and integrals.
Demonstration of solving the integral of x sine x by applying the integration by parts formula.
Repetition of the integration by parts process to solve more complex integrals.
Integration of x squared e to the x using integration by parts and the importance of choosing the right u and dv.
Illustration of the iterative process in integration by parts and the need to reapply the method.
Introduction of a tabular method for simplifying integration by parts with powers of x.
Explanation of the tabular method for integration by parts, emphasizing its ease of use with powers of x.
Application of the tabular method to integrate x squared e to the x, demonstrating its effectiveness.
Handling of integration with limits, emphasizing the process of integrating first and then evaluating the limits.
Example of integrating x sine x with limits from 0 to pi/2, showing the evaluation process.
Integration of two transcendental functions using integration by parts, highlighting the choice of trigonometric functions as dv.
Demonstration of solving the integral of e to the x cosine x using algebraic manipulation to avoid an infinite cycle.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: