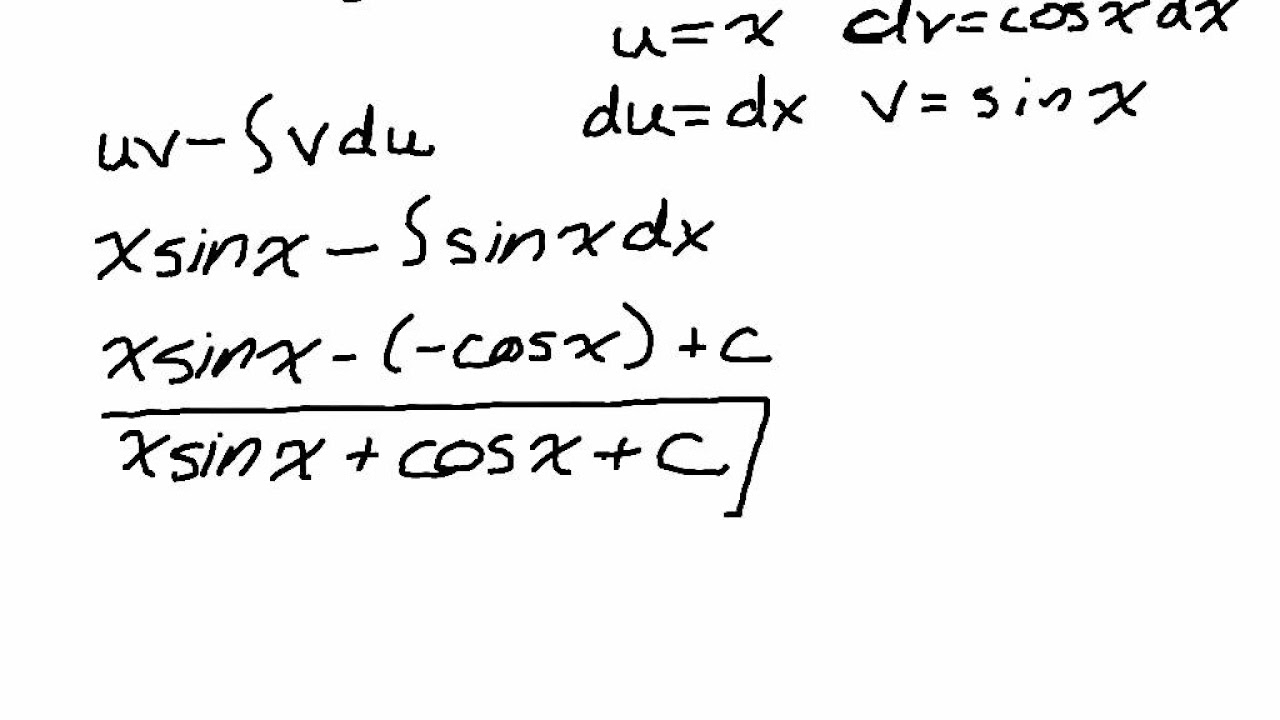4.6 - Integration Techniques - Integration by Parts
TLDRThe video script offers an in-depth exploration of the integration by parts technique, a method used to integrate products of functions that arise from differentiation using the product rule. It emphasizes the importance of selecting the correct 'u' and 'dv' functions to simplify the integral. The script guides viewers through the process of differentiating 'u' and integrating 'dv', then rearranging the formula to solve for the desired integral. It highlights the need for trial and error in choosing the right pair of functions, as an incorrect choice can lead to a more complex integral. The video uses examples, including integrals of 'x times e^x' and 'x times the natural log of x', to illustrate the technique. It also discusses the application of integration by parts to definite integrals, noting the need to reapply limits of integration after variable substitution. The script concludes by acknowledging the limitations of integration by parts and the necessity of computational methods for some complex integrals.
Takeaways
- 📚 Integration by parts is an alternative technique used when the function to be integrated is a result of differentiation using the product rule.
- 🔁 The process reverses the product rule of differentiation, allowing the integration of products of functions, particularly useful when one part of the product is simpler upon integration or differentiation.
- ⚖️ The formula for integration by parts is \( \int u \, dv = uv - \int v \, du \), where \( u \) and \( dv \) are chosen such that \( u \) can be easily differentiated and \( dv \) can be easily integrated.
- 🔍 Choosing the correct \( u \) and \( dv \) for integration by parts requires insight and often involves trial and error, as the goal is to simplify the integral into a form that can be solved more directly.
- 🌟 A common strategy is to choose \( u \) to be the function that becomes simpler after differentiation (such as \( \ln(x) \) or \( x \)) and \( dv \) to be the function that can be easily integrated (like polynomials or exponential functions).
- 📉 When applying integration by parts, the integral of the derivative of \( u \) with respect to \( x \) effectively cancels out, leaving you with the original function \( u \) times \( v \).
- 🤔 The challenge in using integration by parts is finding the right combination of \( u \) and \( dv \) that simplifies the integral, which may require multiple attempts and a good understanding of what simplifies upon integration or differentiation.
- ⛓ The process can be iterative, requiring multiple applications of integration by parts, especially when the resulting integral from the first application is of a form that still requires integration by parts.
- 📌 It's important to remember that not all integrals can be solved using elementary functions; some integrals may require numerical methods or computer algorithms for approximation.
- 🧮 For definite integrals, the limits of integration must be applied to every term resulting from the integration by parts process, and the final answer should reflect the evaluation of these limits.
- 📐 The technique is particularly powerful for integrals that do not fit the standard forms solvable by basic integration formulas, such as the power rule, and can handle more complex functions resulting from the product rule.
Q & A
What is the main purpose of using integration by parts?
-Integration by parts is primarily used to integrate a set of functions that result from differentiation via the product rule. It allows us to break down complex integrals into simpler ones that can be solved directly using known integration techniques.
How does the formula for integration by parts relate to the product rule in differentiation?
-The formula for integration by parts is essentially the reverse of the product rule in differentiation. While the product rule states that the derivative of a product of two functions is the first function times the derivative of the second plus the second function times the derivative of the first, integration by parts rearranges this to solve for the integral of the product of the two functions.
What are the general steps to apply integration by parts?
-To apply integration by parts, one must: (1) choose functions u and dv such that u can be easily differentiated and dv can be easily integrated, (2) compute the derivative of u (du) and the antiderivative of dv (v), (3) apply the integration by parts formula ∫udv = uv - ∫vdu, and (4) solve the resulting simpler integrals.
Why is it necessary to choose the correct u and dv for integration by parts?
-The correct choice of u and dv is crucial because it determines whether the resulting integral after applying the integration by parts formula will be simpler and solvable. If the choice leads to a more complicated integral, it indicates that a different pair should be chosen.
How does the process of choosing u and dv in integration by parts involve trial and error?
-Trial and error is involved in choosing u and dv because one must select functions that, when differentiated or integrated, result in a simpler integral. Sometimes the initial choice may not simplify the integral, requiring a different combination to be tried until a simpler integral is obtained.
What is the role of substitution in the context of integration by parts?
-Substitution is not directly a part of the integration by parts method. However, it can be used in conjunction with integration by parts when the integral of dv involves a nested function or a form that requires substitution to simplify before integrating.
Can you provide an example of a function that would be a good choice for u in integration by parts?
-A good choice for u in integration by parts would be a function that simplifies upon differentiation. For instance, if the integrand involves both x and e^x, choosing e^x as u would be beneficial because its derivative is e^x, which is simpler than the original function.
What is the significance of the antiderivative in the process of integration by parts?
-The antiderivative plays a crucial role in integration by parts as it allows us to reverse the process of differentiation. Specifically, we find the antiderivative of dv to get v and the derivative of u to get du, which are then used in the integration by parts formula to simplify the original integral.
What happens when the integral generated after applying integration by parts is more complicated than the original integral?
-If the integral generated is more complicated, it indicates that the chosen functions for u and dv are not suitable. In such a case, one should revert to the original integral and try a different combination of u and dv to find a simpler integral.
How does the process of integration by parts apply to definite integrals?
-For definite integrals, after applying the integration by parts formula and simplifying the resulting expression, you evaluate the simplified expression at the upper and lower limits of integration. The limits of integration do not change during the integration by parts process.
What is the final step in solving an integral using integration by parts?
-The final step is to evaluate the resulting simpler integral, which may involve further integration by parts, substitution, or direct application of known integration formulas. Once the antiderivative is found, it is used to find the definite integral's value if applicable.
Outlines
📚 Introduction to Integration by Parts
This paragraph introduces the concept of integration by parts, contrasting it with the substitution technique previously discussed. It explains that integration by parts is used for integrating functions derived from the product rule, emphasizing the importance of understanding the product rule for successful application. The paragraph outlines the formula for differentiating a product of two functions, u and v, and how anti-differentiation can revert this process. It also touches on the idea of integrating both sides of the differentiation formula with respect to x, leading to the integral of the product of u and dv, and v and du.
🔍 Understanding the Integration by Parts Formula
The second paragraph delves into the integration by parts formula, illustrating how to rearrange the formula to solve for the integral of u dv. It discusses the goal of simplifying the integrand into a product of two functions and an easier integral to solve. The paragraph stresses the importance of choosing the correct functions for u and dv, where u should be a function that simplifies upon differentiation, and dv should be a function that can be integrated without becoming overly complicated. It acknowledges that finding the right pair may require trial and error and encourages trying different combinations until a suitable pair is found.
🎯 Application of Integration by Parts with Examples
The third paragraph focuses on applying the integration by parts formula through examples. It starts with a basic example of integrating x times e to the x with respect to x. The paragraph explains the process of choosing u and dv, finding their derivatives and integrals, and then substituting these into the integration by parts formula. It also discusses the importance of the new integral being simpler to solve than the original, and how different combinations of u and dv can lead to more or less complicated integrals.
🔁 Exploring Different Combinations for u and dv
This paragraph explores different combinations for u and dv in the context of integration by parts. It discusses the process of choosing u to be e to the x and dv to be x dx, and the subsequent steps to find du, dv, and the anti-derivatives. The paragraph illustrates that the choice of u and dv can significantly affect the complexity of the resulting integral and emphasizes that the goal is to simplify the integral for direct evaluation using known techniques.
📉 Integration by Parts with Natural Logarithm Functions
The fifth paragraph addresses the application of integration by parts with natural logarithm functions. It explains that the natural logarithm function cannot be directly integrated, thus it must be part of u. The paragraph outlines the process of differentiating the natural logarithm function and integrating dv, which in this case is 1 dx. It also discusses the importance of the new integral being simpler than the original, and how the process may involve trial and error to find the correct u and dv.
🧩 Solving Definite Integrals Using Integration by Parts
The sixth paragraph discusses the application of integration by parts to definite integrals. It emphasizes that the limits of integration apply to the entire problem when using the formula and that the final answer should take into account the limits from the original integral. The paragraph provides an example of integrating x cubed times the natural log of x from one to two, showing how to apply the integration by parts formula and evaluate the result at the given limits.
🔢 Final Evaluation and Conclusion
The final paragraph concludes the discussion on integration by parts. It reiterates the importance of the technique alongside integration by substitution for solving anti-derivative problems that do not fit standard rules. The paragraph acknowledges the inherent complexity of integration and the reality that some problems may require computer assistance. It encourages trial and error in selecting the components for the integration by parts formula and reminds learners that not all functions can be integrated by hand.
Mindmap
Keywords
💡Integration by Parts
💡Product Rule
💡u-substitution
💡Differential
💡Antiderivative
💡Function
💡Simpler Integral
💡Trial and Error
💡Differentiation
💡Integrand
Highlights
Integration by parts is an alternative technique for integrating functions resulting from the product rule differentiation.
The technique is particularly useful for functions that are products of two other functions, u and v, where v is the function being differentiated in the product rule.
Integration by parts reverses the product rule of differentiation, allowing for the simplification of complex integrals.
The formula for integration by parts is ∫udv = uv - ∫vdu, which rearranges the product rule formula for differentiation.
Choosing the correct u and dv functions is crucial for the success of integration by parts and often requires trial and error.
The goal is to choose u and dv in such a way that the resulting integral after applying the formula is simpler to solve.
When integrating by parts, the function u should be one that simplifies upon differentiation, and dv should be a function that can be easily integrated.
The process involves differentiating u to get du and integrating dv to get v, then substituting these into the integration by parts formula.
Integration by parts can be applied to a variety of functions, including those involving exponential functions, logarithms, and polynomials.
The technique may require multiple iterations to find the correct u and dv functions that result in a simpler integral.
Examples are provided to illustrate the process of choosing u and dv, differentiating and integrating these functions, and applying the formula.
In some cases, the integral resulting from integration by parts can be further simplified using substitution or other integration techniques.
The video emphasizes the importance of practice and repetition in mastering the technique of integration by parts.
The presenter demonstrates the process with several examples, including integrals of the form x*e^x and x*ln(x), to show different strategies for choosing u and dv.
Integration by parts is a powerful tool for solving integrals that do not conform to the basic rules of integration, expanding the scope of solvable integrals.
The video concludes with a reminder that while integration by parts and substitution are versatile, they are not exhaustive and some integrals may require computer assistance.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: