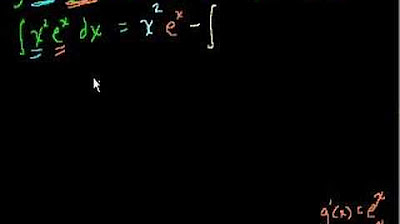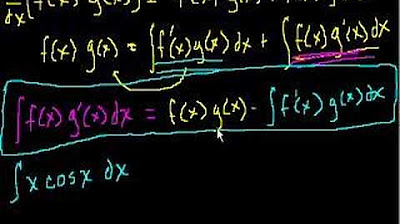integration by parts, DI method, VERY EASY
TLDRThe video script presents a detailed walkthrough of the integration by parts method, illustrating it with three examples. The first example demonstrates integrating a product of functions using the DI method, where sine of 3x is integrated and x squared is differentiated. The second example shows how to apply integration by parts to a product of x to the fourth power and ln(x), emphasizing when to stop the process. The third example tackles the integral of x times sine x, showcasing the iterative process and highlighting when to cease differentiation. The script effectively communicates the steps and decision-making involved in integration by parts, providing clear explanations and emphasizing the importance of recognizing when a row's product can be directly integrated.
Takeaways
- 📚 Integration by parts is a technique used to integrate functions that are products of two functions, where one function is easy to integrate and the other is easy to differentiate.
- 🔄 The DI method involves breaking down the integral into two parts: one part to differentiate (D) and the other to integrate (I).
- 🌟 The process alternates signs on the diagonal of the DI table, starting with a plus and then alternating with minus signs.
- 📈 When using the DI method, you should choose the part of the integral that is harder to integrate for integration first.
- 🛑 If the differentiation of a part results in zero, the process stops, as further differentiation will not contribute to the result.
- 🔢 The answer is constructed by multiplying the diagonals of the DI table along with the alternating signs and adding the results.
- 🌐 In the example with x^2 * sin(3x), the integral of sin(3x) is found first, and then x^2 is differentiated.
- 📊 For the integral of x^4 * ln(x), the choice between integrating ln(x) or differentiating x^4 doesn't affect the final result.
- 🥂 When a function part repeats in a row, you stop the process, as further integration by parts will not simplify the expression.
- 🧩 The final answer includes the product of the diagonals, the alternating signs, and any remaining integrals that need to be evaluated.
- 🎓 The process is demonstrated with three examples, each illustrating different scenarios and steps in the integration by parts method.
Q & A
What is the main topic of the video?
-The main topic of the video is explaining the process of integration by parts using the DI method.
Why is substitution not recommended for the first example given in the video?
-Substitution is not recommended for the first example because if we let u equal 2x, the derivative of the function (3x) would cancel with the x^2, making it impossible to proceed with the integration.
What do the D and I in the DI method stand for?
-In the DI method, D stands for the part of the integral that you will differentiate, and I stands for the part that you will integrate.
How does the video demonstrate the first step of using the DI method?
-The video demonstrates the first step by selecting the integral of x^2 * sin(3x), deciding to integrate sin(3x) first, and differentiating x^2. It then shows the process of filling out the DI table and stopping when a zero appears in the D column.
What is the role of the plus-minus signs in the DI table setup?
-The plus-minus signs in the DI table setup are used to alternate the signs of the terms as you fill out the table. This helps in keeping track of the signs when constructing the final answer from the table.
How does the video address the second example involving the integral of x^4 * ln(x)?
-The video addresses the second example by choosing to integrate ln(x) first and differentiate x^4. It shows the process of filling out the DI table and stopping when the product of a row can be integrated, which in this case is when we get 1/5x^5 after integrating x^4 and 1/x after differentiating ln(x).
What is the significance of the zero in the D column in the DI method?
-The zero in the D column signifies that the differentiation of the chosen part has resulted in a constant, which means the process can be stopped as no further differentiation is needed, and the current row can be used to construct the answer.
How does the video handle the third example involving the integral of x * sin(x)?
-In the third example, the video chooses to integrate sin(x) and differentiate e^x. It shows the process of filling out the DI table and stopping when a function part repeats, indicating that the differentiation has resulted in a term that can be integrated, leading to the construction of the final answer.
What is the final result of the integral of x * sin(x) as presented in the video?
-The final result of the integral of x * sin(x) is -e^x * cos(x) + e^x * sin(x) + (1/2) * integral of e^x * sin(x) dx, with the addition of a constant C at the end.
How does the video emphasize the importance of careful integration in the DI method?
-The video emphasizes the importance of careful integration by showing how easy it is to make mistakes with the alternating signs, especially when dealing with trigonometric functions like sine and cosine. It encourages double-checking and careful consideration of the derivatives and integrals involved.
What is the role of the constant C in the final answer of integration by parts?
-The constant C is added at the end of the final answer to account for the constant of integration that is always present in indefinite integrals. It represents the arbitrary constant that can be added to any indefinite integral.
Outlines
📚 Introduction to Integration by Parts
The paragraph introduces the concept of integration by parts, focusing on the DI method. It explains the process through an example of integrating x^2 * sin(3x). The speaker emphasizes that substitution is not ideal for this integral and demonstrates the first step of integration by parts, which involves differentiating one part (D) and integrating the other (I). The explanation includes setting up the DI table, alternating signs, and stopping when a zero appears in the D column. The example concludes with the integral of sin(3x) resulting in -1/3 cos(3x), and the antiderivative of x^2 being x^2, leading to the final answer involving products of diagonals and signs from the DI table.
📈 Applying Integration by Parts: Second Example
This paragraph presents a second example to illustrate the DI method, focusing on the integral of x^4 * ln(x). The speaker chooses to integrate ln(x) and differentiate x^4, setting up the DI table with alternating signs. The integral of x^4 is calculated as 1/5 x^5, and the derivative of ln(x) is 1/x. The process continues until the product of the row can be integrated, which is x^4 * ln(x), marking the second stop. The answer is constructed using the product of diagonals and signs, resulting in 1/5 x^5 * ln(x) and a remaining integral that is handled by adding the integral to both sides of the equation, ultimately simplifying to 1/25 x^5 + C.
🔄 Integration by Parts with Trigonometric Functions
The third paragraph delves into another application of integration by parts, this time with the integral of x * sin(x). The speaker decides to integrate sin(x) and differentiate e^x, detailing the process of integrating and differentiating with the DI method. The explanation includes the alternating signs and the importance of stopping when the function part repeats. The final answer is derived by combining the products of the diagonals and the remaining integral, resulting in -e^x * cos(x) + e^x * sin(x) + 1/2 ∫ e^x * sin(x) dx, which simplifies to -1/2 e^x * cos(x) + 1/2 e^x * sin(x) + C after handling the extra integral by multiplying by 1/2 to cancel out the repeated function part.
🎓 Conclusion and Final Thoughts
The final paragraph wraps up the discussion on integration by parts using the DI method. The speaker emphasizes the importance of understanding when to stop the process, either when a zero appears in the D column or when the product of a row can be integrated. The paragraph concludes with a call to action for viewers to subscribe if they enjoyed the video, expressing gratitude for the support.
Mindmap
Keywords
💡Integration by Parts
💡Differentiate
💡Integrate
💡Substitution
💡Antiderivative
💡Di Table
💡Product of the Diagonals
💡Cosine
💡Sine
💡e to the x
💡ln(x)
Highlights
Introduction to the DI method for integration by parts, emphasizing its simplicity and effectiveness.
Explanation that substitution is not suitable for the given example due to the disappearance of the derivative.
Description of the DI method's process, where one part is differentiated and the other integrated.
Demonstration of the first step in using the DI method with the integral of x^2 * sin(3x).
Integration of sin(3x) resulting in -1/3 cos(3x), showcasing the application of the DI method.
Differentiation of x^2 leading to 2x, illustrating the DI method's differentiation step.
Explanation of when to stop in the DI method: when a zero appears in the D column.
Presentation of the final answer for the integral of x^2 * sin(3x) using the DI method.
Introduction of the second example using the DI method for the integral of x^4 * ln(x).
Selection of ln(x) to be integrated and x^4 to be differentiated in the DI method.
Integration of x^4 resulting in 1/5 x^5 and differentiation of ln(x) resulting in 1/x.
Decision to stop the DI method when the function part repeats, preventing an endless cycle.
Presentation of the final answer for the integral of x^4 * ln(x) using the DI method.
Introduction of the third example for the integral of x * sin(x) using the DI method.
Choice to integrate sin(x) and differentiate e^x, demonstrating flexibility in the DI method.
Integration and differentiation steps for the third example, leading to a repeating function part.
Explanation of how to handle the repeating function part and the addition of the integral e^x * sin(x) dx.
Final answer for the integral of x * sin(x) using the DI method, including the integral part.
Summary of the three situations demonstrating the DI method for integration by parts, emphasizing its practical application.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: