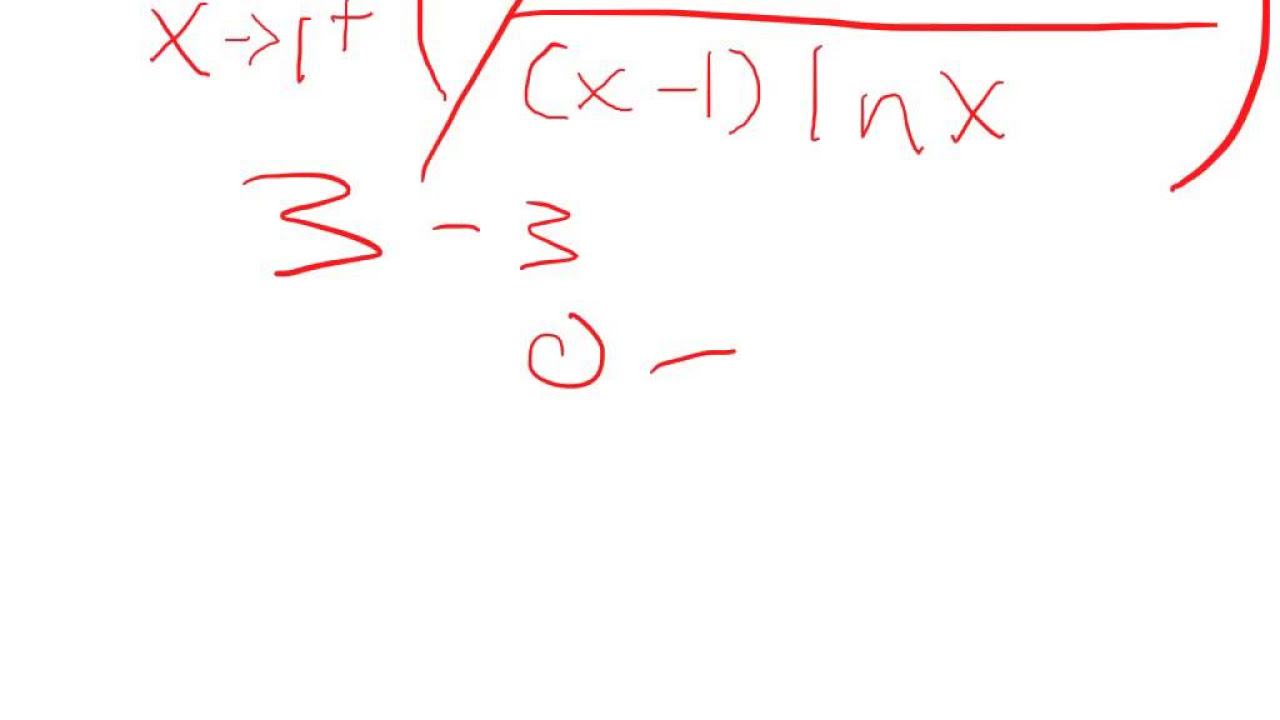L'Hopital's Rule (Other Indeterminate Forms)

turksvids
1 Jun 201306:19
EducationalLearning
32 Likes 10 Comments

TLDRThis video script discusses the application of L'Hôpital's Rule to evaluate limits involving exponential functions with indeterminate forms. The technique involves taking the natural log of the expression, applying L'Hôpital's Rule, and then exponentiating the result. Two examples are provided, demonstrating the process step-by-step.

Takeaways
  • 📚 The script discusses the application of L'Hôpital's Rule to solve indeterminate forms involving exponential functions.
  • 🔍 The first example involves the limit of (1 + sin(x)) to the power of (1/x) as x approaches 0, which is an indeterminate form.
  • 📉 The base of the exponent approaches 1 and the exponent approaches infinity, leading to an indeterminate form of (1^∞).
  • 📝 To tackle this, the script suggests setting the expression equal to Y and taking the natural logarithm of both sides.
  • 🧩 By using properties of natural logs, the exponent is brought down, transforming the expression into a form that can be differentiated.
  • ✂️ L'Hôpital's Rule is then applied by differentiating the numerator and denominator and taking the limit as x approaches 0.
  • 🔢 The derivative of the top and bottom functions are calculated, simplifying the expression to a determinate form.
  • 🔄 The process is repeated until a determinate form is reached, which in the first example results in the limit being 1.
  • 🔃 The limit is then moved inside the natural log and both sides are exponentiated to find the value of Y.
  • 📈 The second example involves the limit of (sin(x) / (3 ln(x))) as x approaches 0 from the right, which also results in an indeterminate form.
  • 📚 The script explains the process of taking the natural log of the expression, differentiating, and applying L'Hôpital's Rule to find the limit.
  • 🎯 The final step in both examples is to exponentiate the result of the natural log to get the original function's limit.
Q & A

  • What is L'Hôpital's Rule used for?

    -L'Hôpital's Rule is used to evaluate limits of the form 0/0 or ∞/∞, which are indeterminate forms, by taking the derivatives of the numerator and denominator.

  • Why do we take the natural log of both sides in the script's first example?

    -Taking the natural log of both sides is a technique to simplify the expression and bring down the exponent, which allows us to apply L'Hôpital's Rule more easily.

  • What is the limit of the first example as X approaches 0?

    -The limit of the first example, as X approaches 0, is e^1, which simplifies to e, because the natural log of e is 1.

  • What is the indeterminate form in the second example of the script?

    -The indeterminate form in the second example is 0^0, which occurs when sine of X approaches 0 and the natural log of X approaches negative infinity.

  • Why is it necessary to remember to exponentiate the final answer after applying L'Hôpital's Rule in the second example?

    -Exponentiating the final answer is necessary because the limit was taken of the natural log of the original expression, and to revert back to the original form, we must undo the natural log by exponentiating.

  • What is the final result of the second example after applying L'Hôpital's Rule?

    -The final result of the second example is e^3, because the limit of the natural log of the expression is 3, and exponentiating e to the power of 3 gives us e^3.

  • How does the script handle the division of the limit in the second example?

    -The script breaks down the division into two separate limits that are easier to evaluate and then multiplies the result by 3, which is a common technique in limit calculations.

  • What property of continuous functions is used to move the limit inside the natural log in the script?

    -The property used is that the limit of a continuous function can be moved inside the function, allowing us to simplify the expression before applying L'Hôpital's Rule.

  • Why is it important to check if the limits used in the division exist before proceeding with the calculation?

    -It's important to ensure that the limits exist because if they don't, the division would be undefined, and the entire calculation would be invalid.

  • What is the basic technique described in the script for evaluating limits with a base to an exponent in an indeterminate form?

    -The basic technique involves taking the natural log of the function, applying L'Hôpital's Rule to evaluate the resulting limit, and then exponentiating the answer to revert back to the original form.

Outlines
00:00
📚 Application of L'Hôpital's Rule in Indeterminate Forms

This paragraph introduces the application of L'Hôpital's rule to solve limits involving exponential functions that result in indeterminate forms. The specific example given is the limit as X approaches 0 of (1 + sin(X))^(1/X). The approach involves setting Y equal to the expression, taking the natural logarithm of both sides, and then applying L'Hôpital's rule to the resulting 0/0 indeterminate form. The process is to take the derivative of the numerator and the denominator, evaluate the limit, and then exponentiate to find the solution.

05:01
🔍 Detailed Example of L'Hôpital's Rule with Natural Logarithms

The second paragraph delves deeper into the application of L'Hôpital's rule with a more complex example: the limit as X approaches 0 from the right of (sin(X)/3) / (ln(X)). This example demonstrates the process of taking the natural log of both sides to bring down the exponent, simplifying the expression, and then applying L'Hôpital's rule to the resulting 0/0 scenario. The solution involves careful manipulation of the limit expressions, ensuring that the limits exist before proceeding, and ultimately exponentiating the natural log to find the final answer.

Mindmap
Keywords
💡L'Hôpital's Rule
L'Hôpital's Rule is a mathematical principle used to evaluate limits that would otherwise be indeterminate, such as 0/0 or ∞/∞. In the video, it is applied to solve limits involving an exponential function where the base approaches 1 and the exponent approaches infinity. The script demonstrates its application in two examples, showing how to transform the original limit into a more manageable form by taking derivatives of the numerator and denominator.
💡Indeterminate Form
An indeterminate form occurs when the limit of a function does not exist in a simple form, such as 0/0 or ∞/∞. The video discusses how to handle such forms, especially in the context of exponential functions, by using L'Hôpital's Rule to find a determinate limit.
💡Natural Logarithm
The natural logarithm, denoted as ln(x), is the logarithm of a number to the base e. In the script, the natural logarithm is used as a tool to transform exponential functions into a form that can be differentiated more easily, which is a crucial step in applying L'Hôpital's Rule.
💡Exponential Function
An exponential function is a mathematical function where the variable is in the exponent. The video script discusses limits involving exponential functions, particularly when the base of the exponent approaches 1 and the exponent approaches infinity, leading to an indeterminate form.
💡Derivative
The derivative of a function measures the rate at which the function's value changes as its input changes. In the context of L'Hôpital's Rule, derivatives are taken of both the numerator and denominator of the original function to resolve the indeterminate form and find the limit.
💡Limit
A limit is a fundamental concept in calculus that describes the value that a function approaches as the input approaches a certain point. The video script focuses on finding limits of functions that exhibit indeterminate forms, using L'Hôpital's Rule as a method to determine these limits.
💡Continuous Functions
Continuous functions are functions that do not have any abrupt changes in value, allowing limits to be taken inside the function without altering the result. The script mentions the property of continuous functions when moving a limit inside a natural logarithm.
💡Sine Function
The sine function is a trigonometric function that describes a smooth, periodic oscillation. In the script, the sine function is used in the context of an example where its value approaches 0, affecting the limit of the function.
💡Cosine Function
The cosine function, like the sine function, is a trigonometric function that represents periodic oscillation. In the script, the cosine function is mentioned in the context of an example where its value approaches 1 as the input approaches 0 from the right, which is used to simplify a limit calculation.
💡Trigonometric Limits
Trigonometric limits are specific limits involving trigonometric functions that often appear in calculus problems. The script provides an example of a trigonometric limit involving the sine and cosine functions, which are fundamental to solving the given problem.
Highlights

Introduction to L'Hôpital's Rule for indeterminate forms involving base to an exponent.

Explanation of the limit as X approaches 0 of (1 + sin(X))^(1/X).

Approaching 1 to the power of infinity as an indeterminate form.

Setting Y equal to the expression to take natural log of both sides.

Using natural logs to simplify the expression and prepare for L'Hôpital's Rule.

Rewriting the expression to apply L'Hôpital's Rule.

Solving the limit using the derivative of the top and bottom functions.

Result of the limit as X approaches 0 is 1.

Moving the limit inside the natural log to find the original expression's limit.

Exponentiating both sides to find the final answer.

Second example involving the limit as X approaches 0 from the right of (sin(X)/3) / (ln(X)).

Approaching 0 to the 0 as an indeterminate form and the application of L'Hôpital's Rule.

Taking the natural log of both sides and simplifying the expression.

Breaking down the expression into two parts for easier application of L'Hôpital's Rule.

Finding the limit of the simplified expression using trigonometric limits.

Multiplying the limits to find the overall limit of the original expression.

Final step of exponentiating the limit of the natural log to find the answer.

Emphasizing the importance of exponentiating the result after finding the limit of the natural log.

Transcripts

Browse More Related Video

L'Hopital's Rule Examples

Applying L'Hopital's Rule to Exponential Indeterminate Forms

Using L'Hopital's Rule to show that exponentials dominate polynomials

Ryan and Nick do L'hopital's rule

Using L'Hopital's Rule on AP Calculus Exam FRQs

L'Hôpital's Rule

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
L'Hopital's RuleCalculusIndeterminate FormsNatural LogLimitsExponentiationTrigonometryLogarithmsMathematicsEducational