L'Hôpital's Rule
TLDRThis video explores L'Hôpital's Rule, a method for evaluating limits involving indeterminate forms like 0/0 and ∞/∞. The presenter explains the rule's application through examples, emphasizing the importance of correctly identifying indeterminate forms and the process of taking derivatives to find limits. The video also includes a graphing calculator demonstration to visually support the mathematical concepts.
Takeaways
- 📚 The video discusses L'Hôpital's Rule, a method for evaluating limits of indeterminate forms such as 0/0 and ∞/∞.
- 🔍 L'Hôpital's Rule is applicable specifically for limits that result in indeterminate forms of 0/0 or ∞/∞, not for all types of indeterminate forms.
- 👨🏫 The presenter mentions that there will be a separate video for other indeterminate forms, which will be linked in the description.
- 📘 The fundamental concept of L'Hôpital's Rule is that if the limit of a fraction results in 0/0 or ∞/∞, the limit can be found by taking the limit of the ratio of their derivatives.
- 📝 The video outlines a three-step process for using L'Hôpital's Rule: identify the indeterminate form, take derivatives of the numerator and denominator, and evaluate the new limit.
- ❗ It's important to avoid stating that the limit equals the indeterminate form (e.g., 0/0) as this is not a real number and can lead to losing points in assessments.
- 🔄 L'Hôpital's Rule may require multiple iterations for some problems, with the presenter noting that two iterations are typically sufficient for AP Calculus exams.
- 📉 The video includes examples demonstrating the application of L'Hôpital's Rule, including classic cases like sin(x)/x as x approaches 0.
- 📈 Graphs are used to visually demonstrate why certain limits equal one, showing that the behavior of functions near the point of interest can predict the limit.
- 🔢 The presenter provides a step-by-step walkthrough of applying L'Hôpital's Rule to various problems, including those requiring iterative application.
- 📚 The video concludes with a challenge for viewers to apply the concepts learned to find a limit involving a given function and its derivatives.
Q & A
What are indeterminate forms?
-Indeterminate forms are expressions that result in an undefined or ambiguous value when evaluated directly. In the context of limits, they include forms like zero over zero, infinity over infinity, infinity minus infinity, zero to the zero power, and infinity to the zero power. These forms often arise when evaluating limits and require special methods, such as L'Hôpital's Rule, to find the actual limit.
Why is L'Hôpital's Rule useful in calculus?
-L'Hôpital's Rule is useful for evaluating limits that result in indeterminate forms, particularly zero over zero and infinity over infinity. It allows you to find the limit by taking the limit of the ratio of the derivatives of the numerator and denominator, rather than dealing directly with the indeterminate form.
What is the first step in applying L'Hôpital's Rule?
-The first step in applying L'Hôpital's Rule is to show that the limit results in an indeterminate form, such as zero over zero or infinity over infinity. This justifies the use of the rule and sets the stage for taking the derivatives of the numerator and denominator.
What is the mistake often made when applying L'Hôpital's Rule?
-A common mistake is to mistakenly apply the quotient rule when taking the derivatives of the numerator and denominator. Remember that L'Hôpital's Rule involves taking the limit of the ratio of the derivatives, not applying the quotient rule to the derivatives themselves.
Can L'Hôpital's Rule be applied repeatedly?
-Yes, L'Hôpital's Rule can be applied repeatedly if the initial application results in another indeterminate form. This might require multiple iterations until a determinate limit is reached or until further applications no longer result in an indeterminate form.
What is the limit of sine x divided by x as x approaches zero?
-Using L'Hôpital's Rule, the limit of sine x divided by x as x approaches zero is found by taking the limit of the ratio of their derivatives, which is cosine x divided by 1. Plugging in x equals zero, the limit is 1.
What happens when you plug in infinity into an expression?
-Plugging in infinity into an expression can lead to indeterminate forms, such as infinity over infinity, which requires the use of L'Hôpital's Rule or other methods to evaluate the limit as the variable approaches infinity.
Why does the limit of e^x over x^n approach zero as x approaches infinity?
-The exponential function e^x grows faster than any power of x. As x approaches infinity, e^x grows much faster than x^n, making the ratio e^x/x^n approach zero.
How does L'Hôpital's Rule help in evaluating the limit of log x minus square root x as x approaches infinity?
-L'Hôpital's Rule can be used to evaluate this limit by taking the derivative of the numerator (1/2 * x^(-1/2)) and the derivative of the denominator (1/x). The resulting limit, as x approaches infinity, is infinity, showing that log x grows slower than square root x.
What is the importance of not saying 'the limit equals zero over zero' in calculus?
-In calculus, stating 'the limit equals zero over zero' is incorrect because it misrepresents the indeterminate form. The correct approach is to show that the limit approaches an indeterminate form and then apply L'Hôpital's Rule or other methods to find the actual limit.
Outlines
📚 Introduction to L'Hôpital's Rule
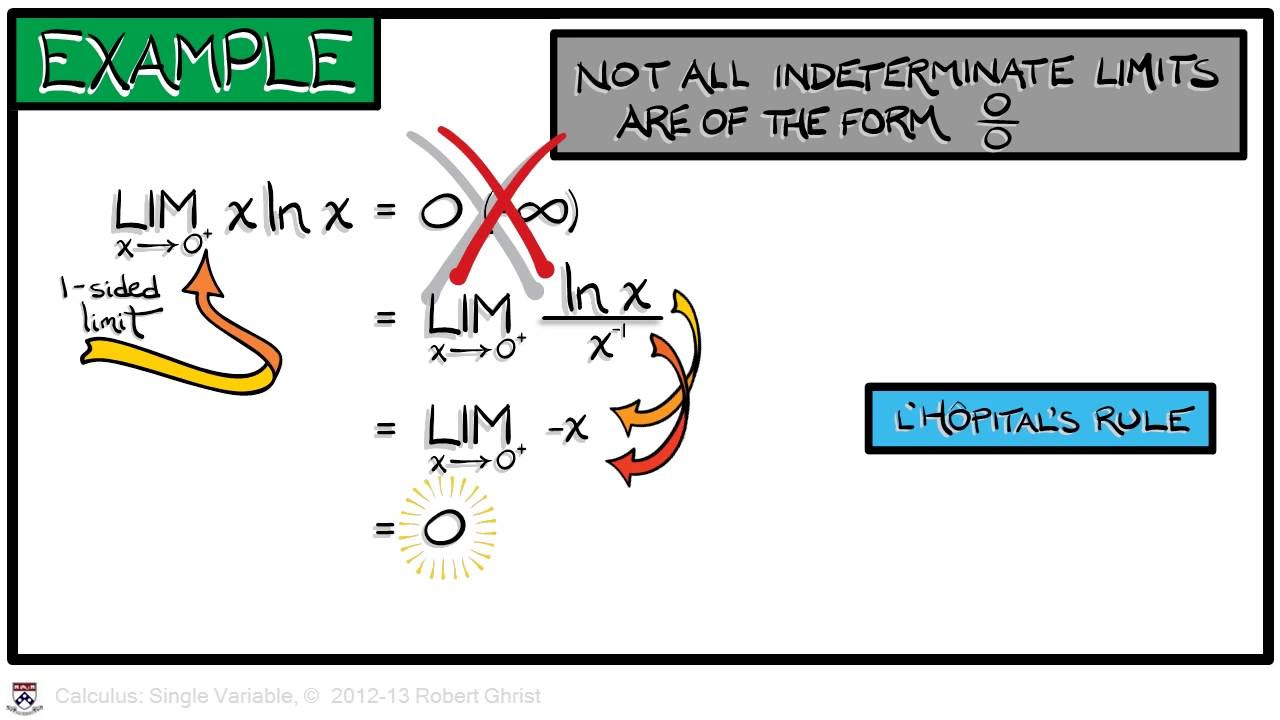
This paragraph introduces the concept of L'Hôpital's Rule, which is used to evaluate limits that result in indeterminate forms such as zero over zero or infinity over infinity. The speaker emphasizes that in AP Calculus, the focus is primarily on 0/0 and ∞/∞ forms. The rule states that if the limit of the numerator and denominator both approach zero or infinity, the limit of the original fraction can be found by taking the limit of the ratio of their derivatives. The speaker also mentions that they will provide a proof of this rule in a separate video and outlines a three-step process for applying L'Hôpital's Rule. An example is given where the limit of sine(x)/x as x approaches zero is evaluated using the rule, resulting in a limit of one.
🔍 Applying L'Hôpital's Rule to Trigonometric Functions
The speaker continues by applying L'Hôpital's Rule to a trigonometric function, specifically the limit of sine(2θ)/3θ as θ approaches zero. The derivative of sine(2θ) is found using the chain rule, resulting in 2cosine(2θ), and the derivative of 3θ is simply 3. The limit is then calculated as two-thirds. The paragraph also covers a more complex example requiring two iterations of L'Hôpital's Rule, involving the limit of e^t - 1 - t over t^2 as t approaches zero. The process involves taking derivatives of the numerator and denominator and plugging in the value of zero, which leads to another indeterminate form, necessitating a second application of the rule. The final limit is found to be one-half.
🎓 Advanced Applications of L'Hôpital's Rule
This paragraph delves into more advanced applications of L'Hôpital's Rule, including a problem that requires two iterations to solve. The speaker provides a hypothetical function f and its derivatives, and asks the viewer to find the limit as x approaches two. The solution involves using L'Hôpital's Rule twice, resulting in a limit of negative one-fourth. Another example involves a particular solution to a differential equation, where the limit of a function g as x approaches one is evaluated. The process requires taking derivatives and using L'Hôpital's Rule to find the limit, which is shown to be zero.
∞ Infinity Over Infinity Limits and Conclusion
The final paragraph addresses infinity over infinity limits, starting with the limit of x as x approaches infinity over e^x. Using L'Hôpital's Rule, the limit is found to be zero, illustrating that e^x grows faster than any power of x. The speaker also mentions that this conclusion can be reached without L'Hôpital's Rule by recognizing the growth rate of e^x. Another example involves the difference between the logarithm of x and the square of x, which also results in an infinity over infinity limit. The speaker uses algebraic manipulation to simplify the expression before applying L'Hôpital's Rule, ultimately showing that the limit approaches infinity. The paragraph concludes with a summary of the examples and a reminder that more resources on L'Hôpital's Rule and other indeterminate forms are available in the video description.
Mindmap
Keywords
💡L'Hopital's Rule
💡Indeterminate Forms
💡Derivatives
💡Limits
💡AP Calculus
💡Trigonometric Functions
💡Exponential Functions
💡Logarithmic Functions
💡Chain Rule
💡Quotient Rule
💡Iterative Application
Highlights
Introduction to L'Hôpital's Rule and its use in evaluating indeterminate forms such as 0/0 and ∞/∞.
Explanation of indeterminate forms, including zero over zero, infinity over infinity, infinity minus infinity, zero to the zero power, and infinity to the zero power.
Focus on 0/0 and ∞/∞ forms in AP Calculus, with a separate video planned for other forms.
L'Hôpital's Rule's first theorem: if the limit of the numerator and denominator both approach zero, the limit of the fraction can be found by taking the limit of the ratio of their derivatives.
Three-step process for dealing with 0/0 and ∞/∞ limits using L'Hôpital's Rule.
Clarification on not equating limits to indeterminate forms like 0/0 or ∞/∞, and the importance of correct justification in exam responses.
Demonstration of applying L'Hôpital's Rule to the classic limit of sine(x)/x as x approaches zero, resulting in a limit of 1.
Use of a graphing calculator to visualize the behavior of functions near the origin, illustrating why the limit of sine(x)/x is 1.
Application of L'Hôpital's Rule to a trigonometric limit involving sine(2θ) and 3θ, resulting in a limit of 2/3.
Example of a limit requiring two iterations of L'Hôpital's Rule, involving e^t and t-related terms.
Guidance on attempting a limit problem involving a differentiable function with given values, encouraging pausing the video for self-practice.
Solution to the practice limit problem, demonstrating the process of applying L'Hôpital's Rule multiple times to reach a conclusion.
Discussion of a limit involving a particular solution to a differential equation, using L'Hôpital's Rule to find the limit as x approaches 1.
Application of L'Hôpital's Rule to an infinity-over-infinity limit, illustrating the concept that e^x grows faster than any power of x.
Algebraic manipulation before applying L'Hôpital's Rule to a limit comparing the growth of log(x) and x^2 near infinity.
Final examples of infinity-over-infinity limits, reinforcing the understanding of growth rates of different functions as x approaches infinity.
Conclusion summarizing the use of L'Hôpital's Rule for zero-over-zero and infinity-over-infinity limits, and the availability of additional resources.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: