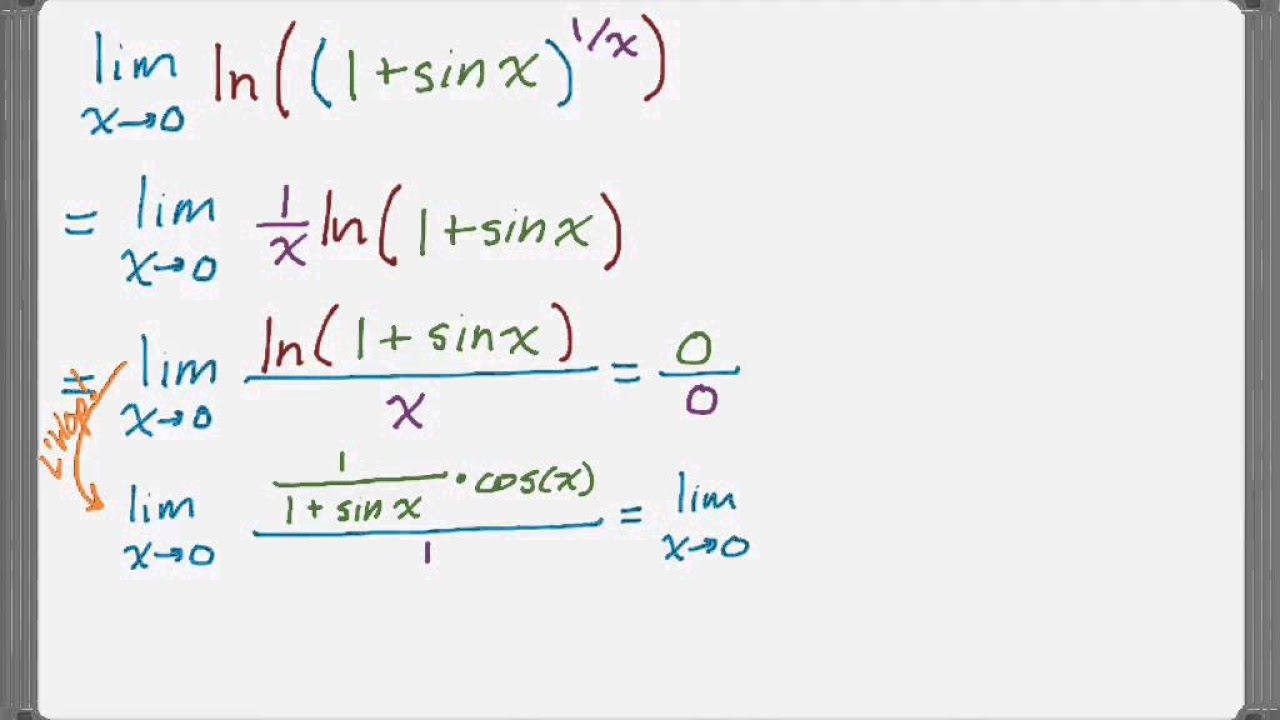Applying L'Hopital's Rule to Exponential Indeterminate Forms
TLDRThe video script discusses the application of L'Hôpital's rule to solve indeterminate forms, particularly focusing on the tricky case of 0^0. The presenter explains that direct substitution results in an indeterminate form and suggests using logarithms to transform exponential expressions into products, which are easier to handle. By taking the natural logarithm of the expression and then applying algebraic manipulations, the form can be converted into a quotient that allows the application of L'Hôpital's rule. The process involves differentiating the numerator and denominator, evaluating the limit, and then using the exponential function to revert back to the original form. The video concludes by emphasizing the importance of recognizing and handling various types of indeterminate forms, highlighting the utility of logarithms in such scenarios.
Takeaways
- 📚 The script discusses an indeterminate form ( x^{sqrt{x}} ) as x approaches 0 from the right, which is not immediately solvable by direct substitution.
- ❗ Direct substitution results in the form ( 0^0 ), which is an indeterminate form with no clear value without further context.
- 🔍 The lecturer uses logarithms to transform the exponential expression into a product, which is easier to handle algebraically.
- 📉 By applying the natural logarithm to the expression, the indeterminate form ( 0^0 ) is converted into ( 0 x (-infinity) ), which is another indeterminate form but a product.
- 🔄 The script demonstrates the conversion of a product into a quotient by algebraic manipulation, setting the stage for the application of L'Hôpital's Rule.
- 🧮 L'Hôpital's Rule is applied to the transformed limit, resulting in a determinate form after taking the derivatives of the numerator and the denominator.
- 📌 The derivatives are computed, leading to a simplification of the expression and eventually to a determinate limit which can be evaluated.
- 🎯 After applying L'Hôpital's Rule, the limit is found to be 0, which is a determinate result.
- ➗ To find the original limit of ( x^{sqrt{x}} ), the natural logarithm must be undone by taking the exponential of the result.
- 🏁 The final evaluated limit of ( x^{sqrt{x}} ) as x approaches 0 from the right is determined to be 1.
- 📈 The script outlines different types of indeterminate forms and the strategies for dealing with them, such as transforming products into fractions or using logarithms for exponential expressions.
- 📘 L'Hôpital's Rule is particularly useful for indeterminate forms that are not directly solvable, like ( 0/0 ), ( infinity/infinity ), and exponential forms involving ( 0 ) or ( infinity ).
Q & A
What is the indeterminate form encountered when plugging in x=0 into the expression x to the power of the square root of x?
-The indeterminate form encountered is 0 to the power of 0, which is undefined as it could be interpreted as either 0 or 1 depending on the context.
Why is the expression 0 to the power of 0 considered indeterminate?
-It is indeterminate because it could be interpreted in multiple ways: as 0 (since any non-zero number to the power of 0 is 0) or as 1 (since 1 to any power is 1).
How does using logarithms help in dealing with exponential indeterminate forms?
-Logarithms convert exponential expressions into products, which are easier to handle. This allows us to manipulate the expression into a form where we can apply standard calculus techniques such as L'Hôpital's rule.
What is the first step in applying L'Hôpital's rule to the given limit?
-The first step is to transform the original limit into a form where L'Hôpital's rule can be applied, which typically involves converting the expression into a quotient of two differentiable functions.
What is the derivative of the natural logarithm of x with respect to x?
-The derivative of the natural logarithm of x (ln(x)) with respect to x is 1/x.
How does the limit change when we take the natural logarithm of both sides of the original limit?
-Taking the natural logarithm of both sides changes the original limit from an exponential form to a product form, which is then further manipulated into a quotient form to apply L'Hôpital's rule.
What is the final result of the limit as x approaches 0 from the right of x to the power of the square root of x?
-After applying a series of algebraic steps and L'Hôpital's rule, the final result of the limit is found to be 1.
Why is it necessary to 'undo' the natural logarithm after applying L'Hôpital's rule?
-The natural logarithm was initially taken to transform the indeterminate form into a more manageable one. After applying L'Hôpital's rule, we revert the logarithm by taking the exponent of the result to find the original limit's value.
What is L'Hôpital's rule used for?
-L'Hôpital's rule is used to evaluate limits of indeterminate forms, particularly those of type 0/0 or ∞/∞, by taking the derivatives of the numerator and denominator.
How can you transform a product of two functions into a quotient to apply L'Hôpital's rule?
-One can transform a product by assigning one of the factors an exponent of -1, effectively making it the denominator, or by factoring out a common term and manipulating it to form a quotient.
What are some examples of indeterminate forms that can be resolved using logarithms?
-Examples include 1 to the power of ∞, ∞ to the power of 0, and 0 to the power of 0. Logarithms can convert these exponential forms into products, which are easier to work with.
What is the general approach to handling different types of indeterminate forms?
-The approach involves recognizing the type of indeterminate form, using algebraic manipulation or logarithms to convert it into a determinate form or a form that allows the application of L'Hôpital's rule, and then evaluating the limit.
Outlines
🔍 Applying L'Hôpital's Rule to Indeterminate Forms
The first paragraph discusses a complex mathematical scenario where the limit as x approaches 0 from the right of x to the power of the square root of x results in an indeterminate form of 0 to the power of 0. The speaker explores the ambiguity of this form and proposes using logarithms to simplify the expression. By taking the natural logarithm of x and manipulating the expression, the indeterminate form is transformed into a quotient, which allows for the application of L'Hôpital's rule. The process involves differentiating the numerator and the denominator and then evaluating the limit, which simplifies to a determinate form. The final step is to compute the limit, which in this case results in 0, and the speaker emphasizes the importance of understanding the process and the transformation from an indeterminate to a determinate form.
🧮 Indeterminate Forms and the Natural Logarithm
The second paragraph elaborates on the process of evaluating limits involving indeterminate forms, particularly those involving exponential functions. The speaker explains how applying L'Hôpital's rule directly to such forms is not always straightforward and requires algebraic manipulations. The paragraph details the use of the natural logarithm to convert exponential expressions into products, which can then be handled more easily. The speaker demonstrates how to apply algebraic tricks to transform products into quotients, making it possible to apply L'Hôpital's rule. After applying the rule and finding a determinate form, the speaker shows how to reverse the natural logarithm process by raising e to the power of the computed limit. The final result of the example is e to the power of 0, which equals 1. The paragraph concludes with a summary of different types of indeterminate forms and the general approach to solving them using L'Hôpital's rule and the natural logarithm.
Mindmap
Keywords
💡Indeterminate form
💡L'Hôpital's rule
💡Natural logarithm
💡Exponential function
💡Derivative
💡Limit
💡Square root
💡Algebraic trickery
💡Zero to the power of zero
💡Infinity
💡e (Euler's number)
Highlights
The limit as x approaches 0 from the right of x to the power of the square root of x is an indeterminate form of the type 0^0.
0 to any nonzero power is 0, while any nonzero number to the power of 0 is 1.
Logarithms can be used to convert exponentials into products, which simplifies the analysis of indeterminate forms.
By taking the natural logarithm, the indeterminate form 0^0 can be transformed into a product of sqrt(x) * ln(x).
As x approaches 0, sqrt(x) approaches 0 and ln(x) approaches negative infinity, resulting in the indeterminate form 0 * -∞.
The trick is to manipulate the expression into a quotient, which allows applying L'Hopital's rule.
Applying L'Hopital's rule by differentiating the numerator ln(x) and denominator x^(1/2) simplifies the expression.
After applying L'Hopital's rule, the limit becomes determinate and can be evaluated by plugging in x=0.
The evaluated limit is 0, which means the original limit of x^(sqrt(x)) as x approaches 0 from the right is e^0 = 1.
Different types of indeterminate forms like 0/0, ∞/∞, ∞-∞, and 0*∞ require different approaches to resolve.
For products like 0*∞, a common technique is to make one factor the denominator with an exponent of -1.
For differences like ∞-∞, multiplying and dividing by a suitable factor to create a denominator can help.
Exponential indeterminate forms like 1^∞, ∞^0, and 0^0 are the trickiest to handle.
Taking the natural logarithm converts exponentials into products, making them easier to work with.
After applying algebraic manipulations and L'Hopital's rule, taking the exponential of the result reverses the natural logarithm step.
L'Hopital's rule can be applied to a wider range of indeterminate forms by using creative algebraic techniques.
The key is to convert the indeterminate form into a determinate form that can be evaluated by plugging in the endpoint.
This approach of using natural logarithms and L'Hopital's rule provides a powerful method for evaluating complex limits.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: