Volume of Solids with Known Cross Sections
TLDRThis video script discusses common volume questions on the AP exam involving solids with known cross-sections. The presenter explains how to set up integrals to find the volume of solids with various cross-sections such as rectangles, squares, semi-circles, and isosceles right triangles, using the region bounded by the x-axis and the graph of y = 7x - x^2 as an example. The script also covers solids with cross-sections perpendicular to the y-axis, including semi-circles formed from the region bounded by y = log(x) and the x-axis. The focus is on understanding how to express the volume as an integral of the area of the cross-sections, without necessarily evaluating the integrals.
Takeaways
- 📚 The video discusses a common type of volume question found on the AP exam involving known cross-sections of solids.
- 📐 The base of the solid is a region in the plane, and the solid's cross-sections are perpendicular to the x-axis or y-axis, with various shapes like rectangles, squares, semi-circles, and isosceles right triangles.
- 🔍 The term 'cross-section' is a key indicator in the problem statement for the type of volume question being addressed.
- 📏 The first example involves a solid with rectangular cross-sections of height 5, derived from a region bounded by the x-axis and a quadratic function.
- 📉 The volume of the solid is calculated using the concept of the Riemann sum, which in the limit becomes an integral of the area of the cross-sections.
- 📚 For the rectangle example, the volume is the integral of 5 times the base with respect to x, where the base is expressed in terms of x from the given function.
- 🔢 The base for the rectangle is given by 7x - x^2, and the integral is set up but not evaluated in the video for time-saving purposes.
- 🔄 The process is repeated for different cross-sections: squares, semi-circles, and isosceles right triangles, each with its own method of setting up the integral.
- 📐 For square cross-sections, the volume integral involves squaring the base function, and for semi-circles, it involves (1/2)πr^2 where r is derived from the function.
- 📉 The video also covers examples with cross-sections perpendicular to the y-axis, such as semi-circles with radius derived from the y-value of a logarithmic function.
- 📝 The final examples include setting up integrals for volumes with isosceles right triangles and squares as cross-sections, emphasizing the importance of correctly identifying the base in terms of the variable of integration.
Q & A
What is the main topic of the video?
-The video discusses a type of volume question commonly found on the AP exam, which involves calculating the volume of solids with known cross-sections.
What is a common characteristic of the problems discussed in the video?
-A common characteristic is that the problems involve a region in the plane that serves as the base of a solid, and the solid has known cross-sections perpendicular to either the x-axis or y-axis.
What is the formula for the volume of a rectangular prism in the context of the video?
-The volume of a rectangular prism is calculated as the area of the base times the height, which in the video's context is represented as 5 times the base (b), where b is the height of the graph at a given x-value.
How is the volume of a solid with square cross-sections calculated?
-The volume is calculated by integrating the area of the square cross-sections with respect to x, where the area is the square of the base (b^2), and b is the height of the graph at a given x-value.
What is the area of a semi-circle used to calculate the volume of a solid with semi-circular cross-sections?
-The area of a semi-circle is half the area of a full circle, which is represented as (1/2) * π * r^2, where r is the radius of the semi-circle.
How do you find the radius of a semi-circle when the cross-sections are perpendicular to the x-axis?
-The radius is found by taking half the difference between the top and bottom of the region at a given x-value, which is expressed as (7x - x^2) / 2 in the video.
What is the area of an isosceles right triangle used to calculate the volume of a solid with such cross-sections?
-The area of an isosceles right triangle is half the area of a square with sides equal to the base of the triangle, represented as (1/2) * (base^2).
How does the video handle the calculation of volume when cross-sections are perpendicular to the y-axis?
-The video provides examples where the volume is calculated by integrating the area of the cross-sections with respect to y, taking into account the height and base of the cross-sections as functions of y.
What is the significance of the word 'cross-section' in the context of the problems discussed in the video?
-The word 'cross-section' is significant as it indicates the shape of the slices taken perpendicular to a given axis (x or y), which is essential for determining the formula used to calculate the volume of the solid.
Can you provide an example of a volume calculation from the video that involves a region bounded by a logarithmic function?
-One example involves a region bounded by y = log(x), the x-axis, and the line x = e^5. The cross-sections perpendicular to the y-axis are semi-circles, and the volume is calculated by integrating (1/2) * π * (e^5 - e^y)^2 with respect to y from 0 to 5.
What is the approach to setting up an integral for the volume of a solid with known cross-sections?
-The approach involves identifying the shape of the cross-sections, expressing the area of these cross-sections as a function of the relevant variable (x or y), and then integrating this area over the specified range to find the total volume.
Outlines
📚 Calculus Volume Problems with Known Cross-Sections
This paragraph introduces a common type of volume problem found on the AP Calculus exam. The video discusses solids formed by regions in the plane with known cross-sections perpendicular to the axes, such as rectangles, squares, and semi-circles. The first example involves a solid with rectangular cross-sections of height five, derived from the region bounded by the x-axis and the graph of y=7x-x^2. The explanation emphasizes the use of Riemann sums and the integral calculus to find the volume, setting up an integral expression but not evaluating it. The approach involves expressing the base in terms of x and integrating the area of the cross-sections over the specified range.
📐 Exploring Solids with Square and Semi-Circular Cross-Sections
The second paragraph continues the discussion on volume problems, focusing on solids with square and semi-circular cross-sections. For the square cross-sections, the base is squared to find the area, and the volume is represented by an integral from zero to seven. The semi-circular cross-sections create a croissant-shaped solid, with the area being half of pi times the radius squared. The radius is expressed in terms of x, and the volume is found by integrating this area from zero to seven. The paragraph also touches on the importance of understanding the approach to these problems rather than the specific shapes of the solids.
📉 Volume Calculations with Isosceles Right Triangles and Logarithmic Functions
This paragraph delves into volume calculations for solids with isosceles right triangle cross-sections and a region defined by a logarithmic function. The isosceles right triangles have their legs perpendicular to the x-axis, and the area is half the square of the base, leading to an integral for volume. The logarithmic function defines a region with cross-sections perpendicular to the y-axis, forming semi-circles. The radius is derived from the function, and the volume is calculated by integrating half of pi times the radius squared with respect to y, from zero to five. The paragraph highlights the process of setting up integral expressions for volume without necessarily evaluating them.
📈 Advanced Volume Problems with Variable Cross-Sections
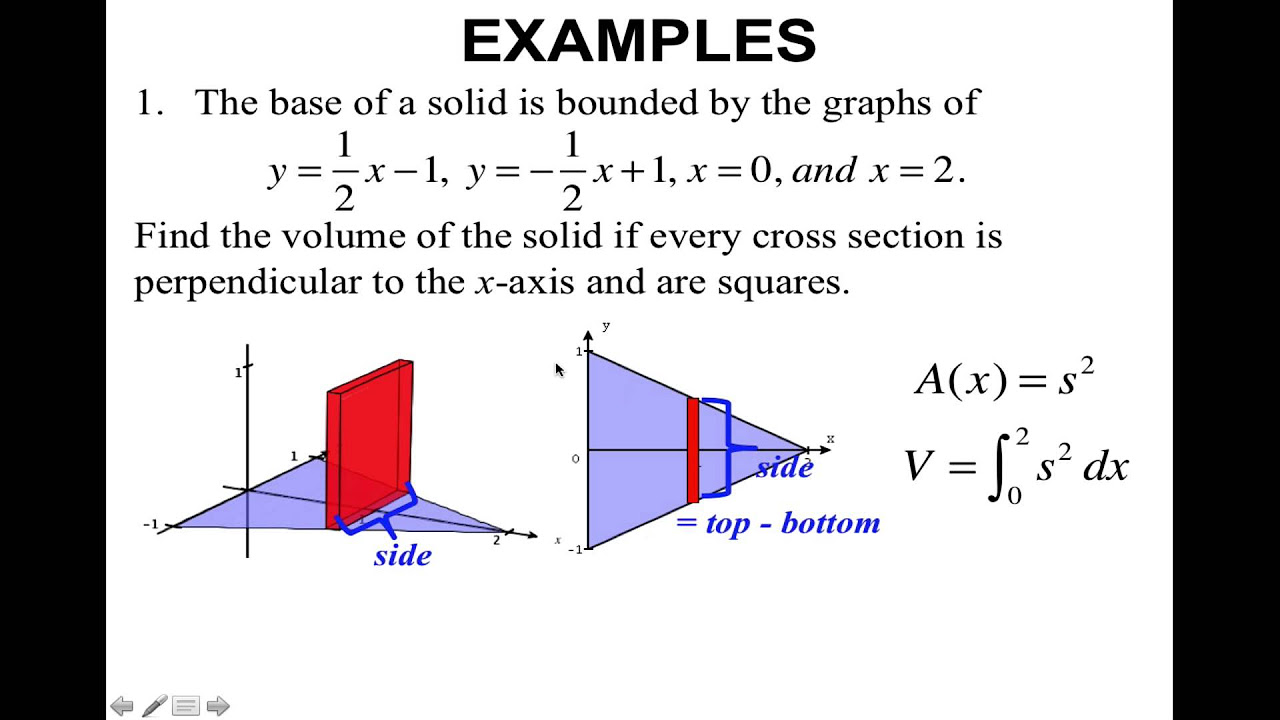
The final paragraph presents more complex volume problems involving regions with variable cross-sections perpendicular to both x and y-axes. It includes a problem where the cross-sections are rectangles with a height dependent on y, and another where the cross-sections are squares with the base derived from a function of y. The paragraph also revisits a 2011 exam question involving a solid with square cross-sections and a base defined by a function of x. The volume is represented by an integral of the square of the base from zero to two. The explanation focuses on setting up the correct integral expressions for these problems, emphasizing the method over the final numerical answers.
Mindmap
Keywords
💡Volume
💡Cross-Sections
💡Riemann Sum
💡Integral
💡Base
💡Solid of Revolution
💡Rectangle
💡Semi-Circle
💡Isosceles Right Triangle
💡Logarithmic Function
Highlights
Introduction to volume questions common on the AP exam involving known cross-sections of solids.
Explaining the concept of cross-sections perpendicular to the x-axis and their impact on solid geometry.
Demonstration of calculating volume using the Riemann sum approach for rectangular prisms.
Illustration of how to find the volume of a solid with rectangular cross-sections by integrating the area.
Introduction to the concept of integrating the area of cross-sections to find the volume of a solid.
Example of calculating volume with cross-sections perpendicular to the x-axis being squares.
Explanation of how to set up an integral to represent the volume of a solid with square cross-sections.
Discussion on the volume calculation of solids with semi-circular cross-sections.
Methodology for integrating the area of semi-circular cross-sections to determine the volume of a solid.
Introduction to isosceles right triangles as cross-sections and their role in volume calculation.
How to set up an integral for the volume of a solid with isosceles right triangle cross-sections.
Exploration of solids with cross-sections perpendicular to the y-axis and their volume calculation.
Example of calculating volume with semi-circular cross-sections perpendicular to the y-axis.
Introduction to the concept of integrating with respect to y for volume calculation in certain solid geometries.
Discussion on the volume calculation of solids with rectangular cross-sections perpendicular to the y-axis.
Methodology for setting up an integral to represent the volume of a solid with rectangular cross-sections perpendicular to the y-axis.
Final example involving the volume calculation of a solid with square cross-sections perpendicular to the x-axis.
Summary of the integral setup for volume calculation in solids with known cross-sections.
Transcripts
Browse More Related Video

Calculus AB/BC – 8.7 Volumes with Cross Sections: Squares and Rectangles

Calculating volume by known cross sections

Finding the Volumes of Known Cross Sections ❖ AP Calculus AB
Calculus AB/BC – 8.8 Volumes with Cross Sections: Triangles and Semicircles
Topic 43-Volumes of Solids with Known Cross Sections

Volume Using Known Cross Sections (Slicing) | Calculus 2 Lesson 5 - JK Math
5.0 / 5 (0 votes)
Thanks for rating: