Topic 43-Volumes of Solids with Known Cross Sections

Calculus BC
23 Dec 201311:43
EducationalLearning
32 Likes 10 Comments

TLDRThe video script is a comprehensive calculus lecture focusing on the calculation of volumes of solids with known cross-sections. The instructor begins by explaining the concept of cross-sections in 3D objects and how they appear when an object is sliced vertically or horizontally. Using the example of a pyramid, the lecture demonstrates how to visualize and calculate the volume of a solid when cross-sections are perpendicular to the x-axis. The process involves integrating the area of the base, represented by the difference between two functions, over the interval defined by the object's boundaries. The lecture covers various geometric shapes, including squares, rectangles, semicircles, quarter circles, isosceles triangles, and equilateral triangles, emphasizing the importance of knowing their area formulas. Practical examples are provided, such as calculating the volume of a pyramid with square cross-sections and a solid with semicircle cross-sections. The instructor also mentions that understanding this topic is crucial for preparing for the second-semester final project, which involves creating 3D models with different cross-section shapes. The lecture concludes with a teaser for the next class, where more examples will be explored visually.

Takeaways
  • 📐 **Cross-Sections in 3D Objects**: A cross-section is a 2D shape obtained by slicing a 3D object either vertically or horizontally.
  • 📈 **Solids on Coordinate Graphs**: When a solid is sliced perpendicular to the x-axis, the cross-sections are squares, which can be visualized on a coordinate graph.
  • 🧱 **Volume Calculation**: The volume of a solid with known cross-sections is found by multiplying the area of the base by the height (change in x or y, depending on the orientation of the cross-section).
  • 👀 **Bird's-Eye View**: To find the area of the base for volume calculation, a bird's-eye view (top-down perspective) is useful, which resembles finding the area between two curves.
  • 📐 **Integration for Volume**: The volume is calculated by integrating the area of the cross-section from one boundary to another (from x=a to x=b or y=c to y=d).
  • 🔢 **Area Formulas**: Knowledge of area formulas for squares, rectangles, semicircles, quarter circles, isosceles triangles, and equilateral triangles is required, as these are not provided on the AP test.
  • 🏗️ **Example: Pyramid Volume**: The volume of a pyramid with square cross-sections is calculated by integrating the square of the difference between the top and bottom functions over the given interval.
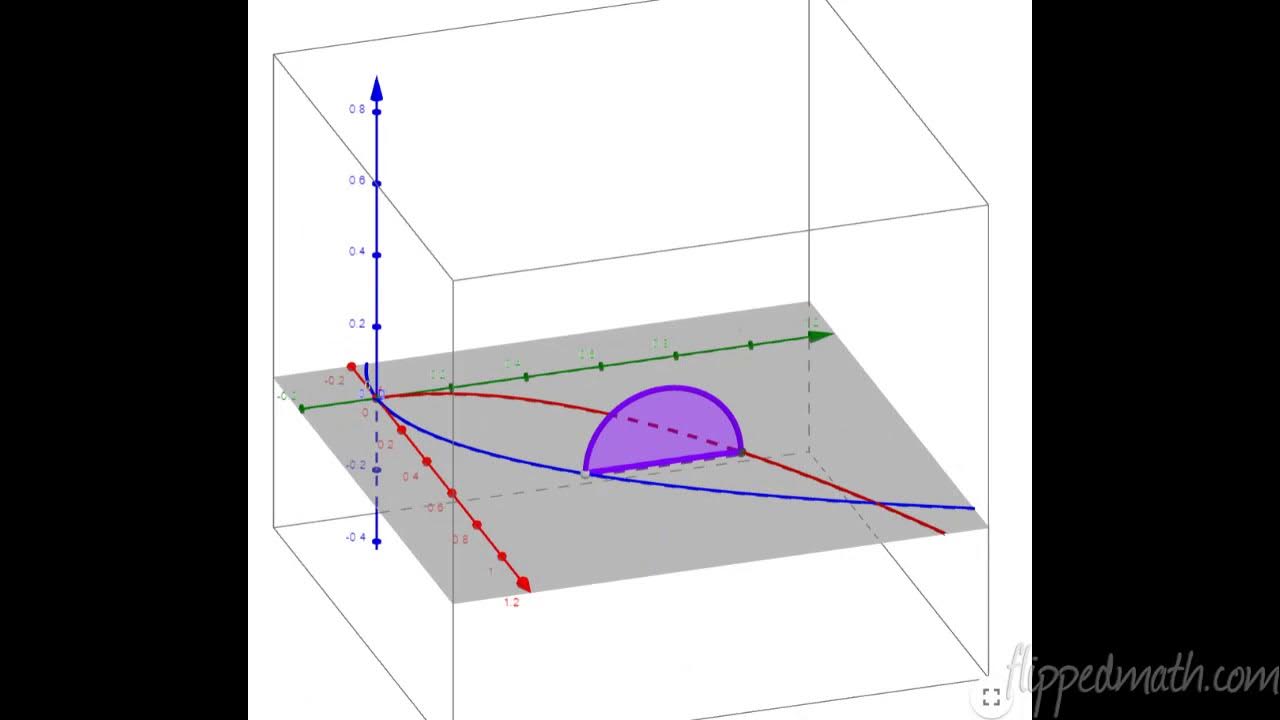
  • 🛕 **Example: Solid with Semicircle Cross-Sections**: For a solid with semicircle cross-sections, the volume is found by integrating the area of a semicircle (π * (radius squared) / 2) between the boundaries defined by the curves.
  • 📉 **Determining Top and Bottom Functions**: To calculate the area of a cross-section, it is crucial to identify which function represents the top and which represents the bottom.
  • 📚 **Geometry Knowledge**: Geometry class knowledge is essential for understanding and applying the formulas for the areas of different shapes.
  • 🎓 **AP Test Preparation**: The concepts covered in this topic are beneficial for preparing for the second-semester final project in calculus, which may involve creating 3D models with specific cross-sections.
Q & A

  • What is a cross-section in the context of 3D objects?

    -A cross-section is a 2D representation obtained by slicing a 3D object either vertically or horizontally.

  • How does the orientation of slicing affect the shape of the cross-section?

    -The orientation of slicing determines the shape of the cross-section; for instance, slicing a pyramid vertically results in equilateral triangles, while slicing it horizontally results in squares.

  • What is the process of turning a pyramid onto its side and cutting it perpendicular to the x-axis?

    -This process involves visualizing the pyramid on its side and then conceptually cutting it into infinite slices perpendicular to the x-axis to create cross-sections.

  • What is the formula for calculating the volume of a solid with known cross-sections?

    -The volume of a solid with known cross-sections is calculated by integrating the area of the cross-section times the change in x (dx) from x=a to x=b, where a and b are the limits of the solid.

  • What is the bird's-eye view used for in the context of calculating volume?

    -The bird's-eye view provides a 2D perspective of the cross-section, which helps in determining the area of the base, necessary for calculating the volume of the solid.

  • What are some of the common 2D geometric shapes and their area formulas that are needed to calculate the volume of a solid?

    -Some common shapes and their area formulas include squares (side^2), rectangles (length * width), semicircles (PI * R^2 / 2), quarter circles (PI * R^2 / 4), isosceles triangles (base^2 / 2), and equilateral triangles (sqrt(3) * base^2 / 4).

  • How do you find the volume of a pyramid with square cross-sections?

    -To find the volume of a pyramid with square cross-sections, you integrate the side length squared (from the top curve minus the bottom curve) with respect to x over the interval defined by the base limits.

  • What is the volume of a pyramid with a base bounded by y = 1/2x - 1, y = -1/2x + 1, x = 0, and x = 2?

    -The volume of the pyramid is 8/3 cubic units, calculated by integrating the square of the difference between the top and bottom curves over the interval from x=0 to x=2.

  • How do you determine the radius of a semicircle cross-section for a solid bounded by two curves?

    -The radius of a semicircle cross-section is half the diameter, which is the difference between the top curve and the bottom curve at a given x-value.

  • What is the area formula used for a semicircle cross-section in the calculation of volume?

    -The area formula for a semicircle is PI * R^2 / 2, where R is the radius of the semicircle.

  • What are some examples of solids with known cross-sections that were mentioned in the script?

    -Examples include Mr. Peanut made with semicircle cross sections perpendicular to the y-axis, a shark's tail or fin made with equilateral triangle cross sections perpendicular to the x-axis, and a bird made with semicircle cross sections perpendicular to the x-axis.

Outlines
00:00
📚 Understanding Cross-Sections and Calculating Volumes

This paragraph introduces the concept of cross-sections in 3D objects and how they can be visualized on a coordinate graph. The video explains the process of slicing a pyramid both vertically and horizontally to obtain 2D cross-sections, which are equilateral triangles and squares respectively. It then demonstrates how to calculate the volume of a single cross-section by considering it as a thin rectangular prism or square. The area of the base is determined using a bird's-eye view, which resembles finding the area between two curves. The volume of the solid is found by integrating the area of the cross-section times the change in X (DX) from a to B, where a and B are the limits of the solid along the x-axis.

05:03
📐 Area Formulas and Volume Calculation Examples

The second paragraph delves into the area formulas for various geometric shapes, including squares, rectangles, semicircles, quarter circles, isosceles triangles, and equilateral triangles. These formulas are essential for calculating the volume of solids with known cross-sections. An example problem is presented where the base of a solid is bounded by certain functions, and the volume is to be found assuming each cross-section is a square perpendicular to the x-axis. The process involves integrating the squared difference between the top and bottom functions over the given interval. Another example is given involving semicircle cross-sections, where the radius is determined by the difference between the top and bottom functions, and the volume is calculated by integrating the area of the semicircle over the interval from -2 to 2.

10:04
🎨 Visualizing Solids with Known Cross-Sections

The final paragraph discusses the application of the previously explained concepts to create 3D models of various shapes, such as Mr. Peanut made with semicircle cross sections, a shark's tail or fin made with equilateral triangles, and a bird also made with semicircle cross sections. These examples serve to illustrate the practical use of the volume calculation methods for different cross-section shapes. The instructor also mentions that the topic will be helpful for preparing for a second-semester final project, which is an actual modeling task. The video concludes with an invitation to the next class and well wishes for the night.

Mindmap
Keywords
💡Cross-sections
Cross-sections refer to the 2D shapes obtained when a 3D object is sliced either vertically or horizontally. In the context of the video, understanding cross-sections is fundamental for calculating the volume of a solid with known cross-sections. The script uses examples of slicing a pyramid to illustrate the concept, showing how the cross-sections can be equilateral triangles or squares depending on the orientation of the cut.
💡Volume
Volume is the measure of the amount of space a solid object occupies. In the video, the main theme revolves around calculating the volume of various solids by integrating the areas of their cross-sections. The script explains that the volume of a geometric shape is found by multiplying the area of the base by the height, and this principle is applied to different cross-sectional shapes like squares and semicircles.
💡Integration
Integration is a mathematical technique used to find the accumulated sum of a function over an interval, which in this video is used to calculate the volume of a solid. The script demonstrates how to integrate the area of a cross-section over a range of x-values (from A to B) to find the total volume of the solid. This process is central to the method of 'disks' or 'washers' for solids with known cross-sections.
💡Solids with known cross-sections
This term refers to a category of geometric solids where the shape of the cross-section perpendicular to a certain axis (like the x-axis or y-axis) is known. The video focuses on finding the volume of such solids by integrating the areas of these known cross-sections. The script provides examples of solids with square and semicircle cross-sections, explaining how their volumes are computed using calculus.
💡Area of the base
The area of the base is the 2D geometric shape that forms the bottom of a solid when it is sliced. The video emphasizes that the volume calculation involves multiplying the area of the base by the height (or the change in x or y depending on the orientation of the cross-section). The script illustrates this with examples of pyramids and other solids, where the area of the base is calculated from the difference between two curves.
💡Bird's-eye view
Bird's-eye view refers to a perspective from directly above, which is used to visualize the 2D shape that forms the base of the solid when looking at it from the top. In the video, this concept is used to help students understand how to find the area of the base from a top-down perspective, which is essential for calculating the volume of the solid.
💡Geometric shapes
Geometric shapes are the fundamental forms in geometry, and they are used to describe the cross-sections of the solids in the video. The script mentions squares, semicircles, rectangles, and triangles as examples of geometric shapes whose areas are needed to calculate the volume of the solid. These shapes are central to the volume calculation process and are used in the integration to find the total volume.
💡Change in X (dx)
The change in X, often represented as dx, refers to the infinitesimal difference in the x-values between two adjacent cross-sections when the solid is being sliced infinitely. In the context of the video, dx is used in the integral to represent the thickness of each infinitesimally thin slice, which when multiplied by the area of the cross-section, gives the volume of that slice.
💡Perpendicular to the x-axis
When the cross-sections of a solid are taken to be perpendicular to the x-axis, it means that each slice is made parallel to the yz-plane. The video uses this orientation to demonstrate how the volume of a solid can be calculated when the cross-sections are squares or semicircles. This orientation is crucial for determining the limits of integration and the shape of the cross-sections.
💡Linear functions
Linear functions are functions of the form f(x) = mx + b, where m is the slope and b is the y-intercept. In the video, linear functions are used to describe the top and bottom boundaries of the cross-sections of the solid. The script shows how to find the area of the cross-section by subtracting the bottom linear function from the top, which gives the side length of the square cross-section.
💡AP test
The AP test refers to the Advanced Placement Exams developed by the College Board, which high school students take to demonstrate college-level mastery of a subject. The video script mentions that students should be familiar with the geometric formulas for areas as they will not be provided during the AP test. This highlights the importance of the topic for students preparing for such exams.
Highlights

Introduction to the concept of cross-sections in 3D objects and their importance in calculating volumes.

Demonstration of slicing a pyramid both vertically and horizontally to obtain different 2D cross-sections.

Visualization of the pyramid on a coordinate graph, showing how to create cross-sections perpendicular to the x-axis.

Explanation of the volume calculation for a single cross-section as the area of the base times the height.

Use of the bird's-eye view to find the area between two curves, which is crucial for determining the base area.

Presentation of the mathematical model for calculating the volume of a solid with known cross-sections.

Differentiation between calculating volumes when cross-sections are perpendicular to the x-axis and y-axis.

List of area formulas for common 2D shapes that are essential for volume calculations.

Application of the area formulas in an example problem involving a pyramid with square cross-sections.

Integration of the area of the cross-section to find the volume of the pyramid.

Guidance on solving a problem with a solid bounded by graphs, involving semicircle cross-sections.

Method for finding the diameter and radius of a semicircle to calculate the volume of the solid.

Integration of the area of a semicircle from given limits to find the volume of the solid.

Discussion on how the topic relates to preparing for the second-semester final project.

Showcase of past projects, including Mr. Peanut made with semicircle cross sections and other geometric solids.

Emphasis on the importance of understanding geometry for success in calculus and AP tests.

Encouragement for students to practice the topic on their own before the next class.

Closing remarks, looking forward to the next class and wishing students a good night.

Transcripts

Browse More Related Video

Volume Using Known Cross Sections (Slicing) | Calculus 2 Lesson 5 - JK Math

Calculating volume by known cross sections

Calculus AB/BC – 8.8 Volumes with Cross Sections: Triangles and Semicircles

Calculus Integrals for Volumes with Known Cross Sections

Calculus AB/BC – 8.7 Volumes with Cross Sections: Squares and Rectangles

Volumes with Known Cross Sections with Calculus, pg 2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusVolumesSolidsCross-Sections3D GeometryIntegrationPyramidsSquaresSemi-circlesGeometry ClassAP TestEducationMath VisualizationProject Preparation