Volume Using Known Cross Sections (Slicing) | Calculus 2 Lesson 5 - JK Math
TLDRThis educational video script introduces viewers to the concept of calculating the volume of solids with known cross-sections using definite integrals. The video begins with a review of the disk method, which is used for solids of revolution with circular cross-sections. It then transitions to more general cases, where cross-sections can be squares, semicircles, rectangles, equilateral triangles, or isosceles triangles. The script provides formulas for the areas of these shapes and illustrates how to set up and solve definite integrals to find the volume of the corresponding solids. Three examples are presented, each involving a different shape of cross-section (square, semicircle, and equilateral triangle) and demonstrating the process of graphing the region, determining the cross-sectional area in terms of the appropriate variable, and integrating to find the volume. The examples are detailed, showing step-by-step calculations and emphasizing the importance of understanding the shape and orientation of the cross-sections relative to the axes. The video concludes with an invitation to view additional examples and to ask questions, reinforcing the educational and interactive nature of the content.
Takeaways
- 📚 The video explains how to calculate the volume of solids with known cross-sections using definite integrals, extending beyond just circular cross-sections.
- 🔄 The disk method previously covered is a specific case for solids of revolution with circular cross-sections, but the same integral principles apply to other shapes.
- ↔️ The method of integration depends on the axis to which the cross-sections are perpendicular: x-axis for sections parallel to x-axis and y-axis for sections perpendicular to y-axis.
- 📏 Common cross-section shapes include squares, semicircles, rectangles, equilateral triangles, and isosceles triangles, each with its own area formula.
- 🔢 For a solid with square cross-sections perpendicular to the x-axis, the volume is found by integrating the side length squared (function of x) with respect to x over the region's x-bounds.
- 🟡 The area formula for a semicircle is πr²/2, where r is the radius, which for a semicircle perpendicular to the y-axis is half the distance from the y-axis to the curve.
- 🟠 For a solid with rectangular cross-sections, the area is the product of the rectangle's height and width, which are functions of the integration variable.
- 🔶 The area of an equilateral triangle is (√3/4) times the side length squared, which is the formula used for cross-sections perpendicular to the x-axis in one of the examples.
- 🚫 It's important to determine the bounds of integration (a and b for x, or c and d for y) based on the region's limits to correctly set up the definite integral.
- 🧮 The process involves setting up the definite integral with the correct cross-sectional area formula, integrating, and then evaluating the integral at the bounds to find the volume.
- 📈 The video provides step-by-step examples to illustrate how to apply these principles to calculate the volume of various solids with different cross-section shapes.
Q & A
What is the main topic of the video?
-The video is about finding the volume of solids with known cross sections using definite integrals.
What are the two methods mentioned for calculating the volume of solids of revolution?
-The two methods mentioned are the disk method and using definite integrals for cross sections that are not circles.
What is the formula for the area of a circle used in the disk method?
-The formula for the area of a circle is pi times the radius squared (πr^2).
How does the shape of the cross sections determine whether we work in terms of x or y?
-We work in terms of x when the cross sections are parallel to the x-axis, and in terms of y when the cross sections are perpendicular to the y-axis.
What are the common shapes of cross sections mentioned in the video?
-The common shapes of cross sections mentioned are squares, semicircles, rectangles, equilateral triangles, and isosceles triangles.
What is the area formula for a square in terms of its side length?
-The area of a square is equal to the side length squared (side^2).
How is the volume of a solid calculated when the cross sections are semicircles perpendicular to the y-axis?
-The volume is calculated using the definite integral from c to d of (1/2)π times the radius squared with respect to dy, where the radius is half the distance from the y-axis to the curve defining the solid.
What is the formula for the area of an equilateral triangle?
-The area of an equilateral triangle is (√3/4) times the side length squared ((√3/4)side^2).
How do you determine the bounds of integration for the volume of a solid with a triangular base and equilateral triangle cross sections?
-You determine the bounds of integration by finding the points where the two functions that define the base intersect, which are the limits between which the x variable lies.
What is the final step in calculating the volume of a solid with known cross sections?
-The final step is to evaluate the definite integral of the cross-sectional area over the bounds of integration to find the volume.
Why is it necessary to graph the region that represents the base of the solid when calculating its volume?
-Graphing the region helps visualize the base and the cross sections of the solid, ensuring accurate setup of the definite integral for calculating the volume.
Outlines
📚 Introduction to Calculating Solid Volumes with Definite Integrals
The video begins with an introduction to finding the volume of solids with known cross sections using definite integrals. It contrasts the disk method, which is used for solids of revolution with circular cross sections, with a more general approach that can handle other shapes. The importance of choosing the correct axis (x or y) for integration based on the orientation of the cross sections is emphasized. Examples are provided to illustrate how to calculate the volume of solids with square and semi-circular cross sections.
🟥 Common Cross-Section Shapes and Their Area Formulas
The video then lists common cross-section shapes—squares, semicircles, rectangles, equilateral triangles, and isosceles triangles—along with their respective area formulas. It highlights the need to memorize these formulas for different cross-section shapes, especially the area formula for an equilateral triangle, which is less commonly used. The video prepares viewers for example problems by ensuring they understand how to calculate the area of various cross sections.
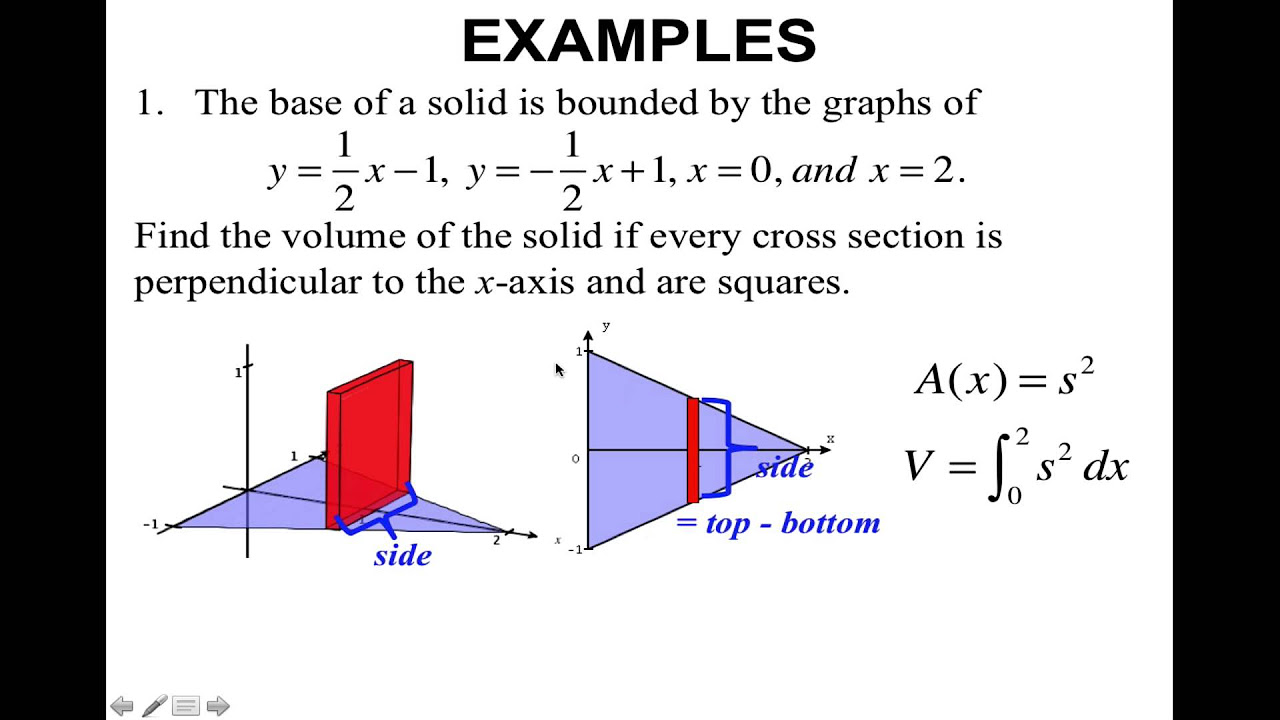
📏 Example 1: Solid with Square Cross-Sections
The first example demonstrates calculating the volume of a solid with a base bounded by the functions y = √x, x = 9, and y = 0, with cross sections that are squares perpendicular to the x-axis. The video shows how to graph the region representing the base of the solid and how to set up the definite integral to calculate the volume. The cross-sectional area is determined by the distance from the x-axis to the function y = √x, and the volume is found by integrating this area from x = 0 to x = 9.
🟦 Example 2: Solid with Semi-Circular Cross-Sections
The second example focuses on a solid with a triangular base bounded by y = (1/2)x, y = 2, and x = 0, with semi-circular cross sections perpendicular to the y-axis. The video illustrates the graphing of the base region and the setup for the definite integral using the area of a semicircle. The radius of the semicircles is determined by half the distance from the y-axis to the boundary line y = (1/2)x. The volume is calculated by integrating the area of the semicircles from y = 0 to y = 2.
🔺 Example 3: Solid with Equilateral Triangular Cross-Sections
The third example involves a solid with a base bounded by y = 4 - x, y = x - 1, and x = 0, with equilateral triangular cross sections perpendicular to the x-axis. The video explains how to graph the base region and determine the length of the sides of the equilateral triangles, which is the distance between the two functions y = 4 - x and y = x - 1. The cross-sectional area is calculated using the area formula for an equilateral triangle, and the volume is found by integrating this area from the lower bound x = 0 to the upper bound where the two functions intersect, x = 5/2.
🧮 Final Calculation and Conclusion
The final part of the video completes the calculation for the volume of the solid with equilateral triangular cross sections. The integral is simplified and solved, resulting in the volume of the solid. The video concludes with an invitation for viewers to check out additional examples and to leave any questions in the comments section. The host signs off, indicating the end of the lesson.
Mindmap
Keywords
💡Definite Integrals
💡Disk Method
💡Cross-Sectional Area
💡Solids of Revolution
💡Volume Calculation
💡Square Cross Sections
💡Semicircular Cross Sections
💡Equilateral Triangle Cross Sections
💡Graphing Regions
💡Integration Bounds
💡Power Rule of Integration
Highlights
Learn how to find the volume of solids with known cross sections using definite integrals.
Review of the disk method for calculating the volume of solids of revolution with circular cross sections.
Introduction to using definite integrals for calculating the volume of non-revolution solids with known cross sections.
Explanation of when to work in terms of x or y depending on the axis the cross sections are perpendicular to.
Demonstration of calculating the volume of a solid with square cross sections perpendicular to the x-axis.
Presentation of the area formulas for squares, semicircles, rectangles, equilateral triangles, and isosceles triangles.
Example problem showing how to find the volume of a solid with a triangular base and semicircle cross sections perpendicular to the y-axis.
Illustration of setting up a definite integral to calculate the volume of a solid with equilateral triangle cross sections.
Detailed walkthrough of solving a definite integral to find the volume of a solid with a triangular base and equilateral triangle cross sections.
Final answer and simplification for the volume of the solid with equilateral triangle cross sections.
The importance of internalizing common cross-sectional area formulas for various shapes.
The process of graphing the region that represents the base of the solid to visualize the problem.
How to determine the bounds of integration for the definite integral representing the volume of the solid.
Using the power rule of integration to solve definite integrals representing the volume of solids.
The application of the method to different types of cross sections, including squares, semicircles, and equilateral triangles.
The significance of understanding how to switch between working in terms of x or y for different cross-sectional orientations.
A comprehensive approach to solving volume problems using definite integrals, applicable to a variety of solid cross sections.
Transcripts
Browse More Related Video

Calculating volume by known cross sections
Topic 43-Volumes of Solids with Known Cross Sections

Calculus Integrals for Volumes with Known Cross Sections

Volume of Solids with Known Cross Sections

AP Calculus AB: Lesson 7.6: Volume using Known Cross Sections

Volumes with Known Cross Sections with Calculus, pg 2
5.0 / 5 (0 votes)
Thanks for rating: