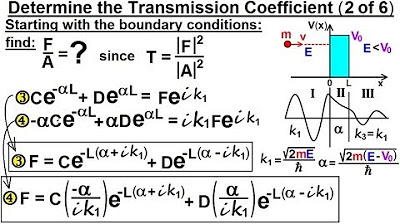
Algebraic Method for Balancing Chemical Equation
TLDRThis educational video script guides viewers through the algebraic method of balancing chemical reactions. It begins by assigning coefficients to elements using letters and then sets up a system of equations based on the occurrences of each element. The script simplifies the system by assigning a value to one variable and eliminating others, ultimately solving for the unknown coefficients. The process is likened to solving a puzzle, with the final balanced reaction provided as a, 4; b, 10; c, 4; d, 1; e, 3, demonstrating a clear and methodical approach to a complex subject.
Takeaways
- 🧪 The video explains how to balance a chemical reaction using the algebraic method.
- 🔤 First, designate letters (a, b, c, d, e) to represent coefficients.
- 🧑🔬 Identify the elements involved in the reaction: magnesium (Mg), hydrogen (H), nitrogen (N), and oxygen (O).
- 📋 Account for the number of times each element appears on both the reactant and product sides.
- 📏 Set up a system of equations based on the occurrences of each element.
- 1️⃣ Assign a value to one of the coefficients to simplify the equations. In this case, a is set to 1.
- 🧮 Substitute and simplify the equations to solve for the other variables (b, c, d, e).
- 🧩 Use elimination and substitution methods to isolate and solve for each variable.
- ✖️ Multiply the equations by necessary factors to eliminate variables and solve the system of equations.
- ✔️ The final coefficients found for the balanced reaction are: a = 4, b = 10, c = 4, d = 1, e = 3.
Q & A
What is the method used in the video to balance a chemical reaction?
-The video uses the algebraic method to balance the chemical reaction.
What are the first steps in balancing a chemical reaction as described in the video?
-The first steps are to designate alphabet letters (a, b, c, d, e) as coefficients and to write down the elements involved in the reaction (Mg, H, N, O).
How does the video suggest to account for each element in the chemical reaction?
-The video suggests to account for each element by noting how many times it occurs on both the reactant and product sides of the reaction.
What is the initial value assigned to the variable 'a' in the video?
-The initial value assigned to the variable 'a' is one.
Why does the video suggest starting with the variable 'a' when balancing the reaction?
-The video suggests starting with 'a' because it only appears once and can be easily isolated, making it a convenient starting point for the balancing process.
What does the video mean by 'simplifying' the equations?
-Simplifying in the video context means to reduce the equations to a form where the coefficients are more manageable and the variables are easier to solve for.
How does the video approach solving for the variable 'b'?
-The video approaches solving for 'b' by using the simplified equations and the known values of other variables to isolate 'b' and find its value.
What technique does the video use to eliminate variables in the system of equations?
-The video uses the technique of multiplying equations by certain factors to eliminate variables and simplify the system.
According to the video, what is the final balanced coefficient for 'a', 'b', 'c', 'd', and 'e'?
-The final balanced coefficients are 'a' = 4, 'b' = 10, 'c' = 4, 'd' = 1, and 'e' = 3.
How does the video ensure that the chemical reaction is balanced correctly?
-The video ensures the reaction is balanced by systematically solving for each variable and checking that the number of atoms for each element is equal on both sides of the reaction.
Outlines
🧪 Balancing Chemical Reactions with Algebraic Method
This paragraph introduces the process of balancing a chemical reaction using algebra. It begins by assigning alphabet letters as coefficients to the reactants and products. The script then instructs to list the elements involved, such as magnesium, hydrogen, nitrogen, and oxygen, and to account for their occurrences on both sides of the reaction. The goal is to set up a system of equations based on these occurrences. The example given uses the variable 'a' to represent the coefficient of magnesium, and assigns it a value of one to simplify the process. This step is crucial for creating a foundation to solve for the remaining coefficients.
🔍 Solving the System of Equations for Balanced Coefficients
The second paragraph delves into solving the system of equations to find the balanced coefficients for the chemical reaction. It starts by simplifying the equations to eliminate variables and isolate one, focusing on the coefficients of hydrogen, nitrogen, and oxygen. The script shows how to manipulate the equations by multiplying and adding them to eliminate certain variables, such as 'e' in this case. The process involves careful algebraic manipulation to find the values of 'b', 'd', and 'e'. The paragraph concludes with the solution for the coefficients: 'a' equals 4, 'b' equals 10, 'c' equals 4, 'd' equals 1, and 'e' equals 3, successfully balancing the chemical equation.
Mindmap
Keywords
💡Balancing chemical reactions
💡Algebraic method
💡Coefficients
💡Elements
💡Reactants and products
💡System of equations
💡Isolating variables
💡Solving equations
💡Conservation of mass
💡Assigning values
💡Simplification
Highlights
Introduction of the algebraic method for balancing chemical reactions.
Designation of alphabet letters to represent coefficients in the reaction.
Identification of elements involved in the chemical reaction: magnesium, hydrogen, nitrogen, and oxygen.
Accounting for the occurrence of each element on both reactant and product sides.
Assigning values to variables by starting with 'a' and setting it to one for simplicity.
Simplification of the system of equations by eliminating variables step by step.
Strategy to isolate one variable by eliminating others through equation manipulation.
Multiplication of equations to facilitate the elimination of variables.
Combining equations to cancel out variables and simplify the system further.
Solving for one variable at a time to progressively find the coefficients.
Use of substitution to find the values of 'b', 'd', and 'e' based on known variables.
Final determination of the coefficients a=1, b=10/4, c=1, d=1/4, and e=3/4.
Explanation of the process to ensure understanding, even for those familiar with the topic.
Efficiency in solving the problem by skipping steps that are clear to the audience.
Emphasis on the importance of each step in the balancing process.
Finalization of the balanced chemical equation with whole number coefficients.
The video's approach to balancing chemical equations in a methodical and educational manner.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: