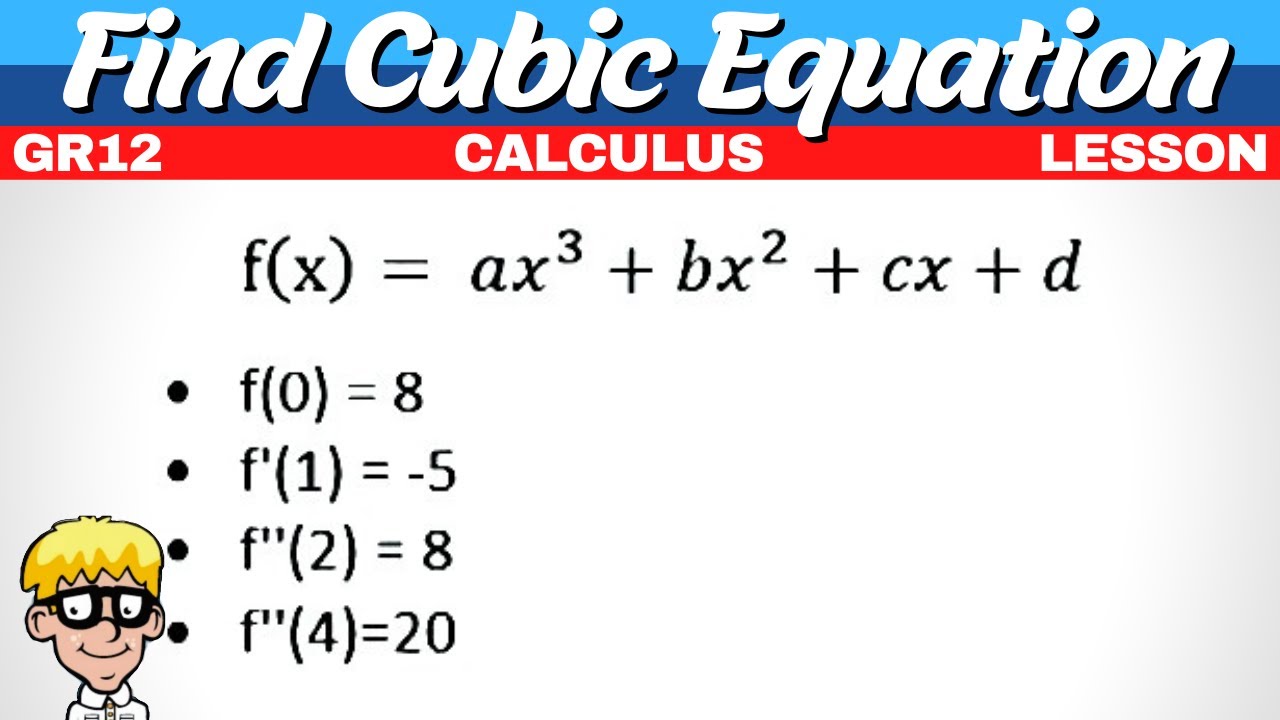Determine Cubic Equation grade 12

Kevinmathscience
20 May 202104:05
EducationalLearning
32 Likes 10 Comments

TLDRThe video script demonstrates how to solve for the coefficients of a cubic equation when given certain points and derivatives. It begins by using a given point to set up an equation, then finds the first and second derivatives, using additional points to create more equations. The script guides through the process of solving these equations simultaneously to find the values of a, b, c, and d, ultimately revealing the original cubic function. It emphasizes the methodical approach of plugging in points and simplifying equations to determine the function's coefficients.

Takeaways
  • 📚 The video discusses a method for solving an equation when x-intercepts are not given but certain points are provided.
  • 🔍 The 'bracket method' is mentioned as a technique for solving equations when x-intercepts are available, but it's not applicable in this case.
  • 📝 The process involves plugging given points into the original equation to derive new equations involving the coefficients.
  • 🔢 The first point given is when x is 2, y is 0, which is used to create an equation with the coefficients a, b, c, and d.
  • 📈 The first derivative of the original equation is found and used to create another equation by substituting x with -2 and equating it to 8.
  • 📉 The second derivative is calculated and used to create two more equations by substituting x with 1 and 2, with the results being 1 and 4, respectively.
  • 🔗 The second derivative equations are solved simultaneously to find the values of coefficients a and b.
  • 🔍 After finding a and b, they are substituted back into the first derivative equation to solve for c.
  • 🔑 The original equation is then used again with the found values of a, b, and c to solve for the last coefficient, d.
  • 🎯 The final equation is constructed using the solved coefficients a, b, c, and d, resulting in a cubic function for f(x).
  • 📝 The final function is f(x) = 0.5x^3 - x^2 - 2x + 4, which is derived step by step using the given points and derivatives.
Q & A

  • What is the 'bracket method' mentioned in the script?

    -The 'bracket method' is a technique used to find the coefficients of a polynomial when the x-intercepts are known. It involves creating a system of equations by substituting the x-intercepts into the polynomial equation and solving for the coefficients.

  • Why can't the bracket method be used in this particular case?

    -The bracket method cannot be used in this case because the x-intercepts are not provided. Instead, the script discusses using given points to determine the coefficients of the polynomial.

  • What is the purpose of finding the first and second derivatives of the original equation?

    -The first and second derivatives are used to find additional points and slopes that can be used to construct the original polynomial equation. The first derivative gives the slope at a given point, and the second derivative can provide information about the concavity and points of inflection.

  • How does the script use the given points to find the coefficients of the polynomial?

    -The script substitutes the given x and y values into the original equation and its derivatives to create a system of equations. By solving these equations simultaneously, the coefficients a, b, c, and d of the polynomial can be determined.

  • What is the significance of the point (2, 0) in the script?

    -The point (2, 0) is significant because it is used to set the y value to 0 in the original equation, allowing the creation of an equation that will help solve for the coefficients.

  • How is the first derivative of the polynomial used in the script?

    -The first derivative is used by substituting x = -2 into it and equating the result to 8, which gives an equation involving the coefficients a and b.

  • What role does the second derivative play in the script?

    -The second derivative is used to create two more equations by substituting x = 1 and x = 2 into it and equating the results to 1 and 4, respectively. These equations help in finding the values of a and b.

  • What is the process of solving the system of equations obtained from the derivatives?

    -The process involves isolating one variable in one of the equations and substituting its value into the other equations. This is done iteratively until all coefficients are determined.

  • How does the script find the value of 'a'?

    -The script finds the value of 'a' by solving the equation obtained from the second derivative when x = 2, which simplifies to 6a = 3, thus a = 0.5.

  • What is the final polynomial function obtained from the script?

    -The final polynomial function is f(x) = 0.5x^3 - x^2 - 2x + 4, which is derived by substituting the found values of a, b, c, and d into the original equation.

Outlines
00:00
📚 Finding Coefficients with Given Points

The paragraph discusses a method for finding the coefficients of an equation when x-intercepts are not provided but specific points are. The process involves substituting the given points into the equation to derive a system of equations. The first point given is (2, 0), which is used to create an equation involving the coefficients a, b, c, and d. The paragraph also mentions using the first and second derivatives to create additional equations, which are then solved simultaneously to find the values of a, b, and c. The process is detailed, showing each step of the calculation and the final values obtained for the coefficients.

Mindmap
Keywords
💡Equation
An equation is a mathematical statement that asserts the equality of two expressions. In the video, equations are used to represent the original function and its derivatives, which are essential for finding the coefficients of the function based on given points.
💡X-intercepts
X-intercepts, also known as roots, are the points where a graph of a function crosses the x-axis. In the context of the video, the absence of x-intercepts is noted, indicating that a different method must be used to solve for the function's coefficients.
💡Bracket Method
The bracket method is a technique used to find the coefficients of a polynomial when its x-intercepts are known. The video mentions this method but clarifies that it's not applicable in this case due to the lack of x-intercept information.
💡First Derivative
The first derivative of a function measures its rate of change at any given point. In the video, the first derivative is used to find additional equations that relate to the coefficients of the original function by plugging in a specific value of x.
💡Second Derivative
The second derivative of a function provides information about the concavity and points of inflection. The video uses the second derivative to create another equation that helps in determining the coefficients of the function by evaluating it at a specific x-value.
💡Plugging Points
In the context of the video, 'plugging points' refers to the process of substituting given x and y values into the equations to form a system of equations that can be solved for the unknown coefficients of the polynomial.
💡Coefficients
Coefficients are the numerical factors in a term of a polynomial. The video's main objective is to determine the coefficients of the original polynomial function by using given points and derivatives.
💡Solving Simultaneously
Solving simultaneously refers to the process of finding values for variables that satisfy multiple equations at the same time. The video describes this process as a way to find the values of a and b by using the equations derived from the second derivative.
💡Polynomial Function
A polynomial function is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. The video is focused on finding the specific form of a cubic polynomial function given certain conditions.
💡Graph
Although not explicitly mentioned in the transcript, the concept of a graph is implied when discussing x-intercepts and the original function's behavior. A graph visually represents the set of points that satisfy a given equation, in this case, the polynomial function.
💡Rate of Change
The rate of change is a fundamental concept in calculus, describing how much one quantity changes with respect to another. In the video, the first derivative is used to analyze the rate of change of the original function at specific points.
Highlights

The method of finding x-intercepts is discussed, but not applicable in this scenario due to lack of intercepts.

Introduction of the bracket method as an alternative approach for finding derivatives.

Given points are used to plug into the original equation to find coefficients.

The first derivative is calculated from the original equation to find further coefficients.

The second derivative is derived to establish additional equations for solving coefficients.

The process of solving simultaneous equations from the second derivative is explained.

Demonstration of isolating variable 'b' using the second derivative's equations.

Substitution of the found 'b' value into another equation to solve for 'a'.

Calculation of 'a' using the derived equations from the second derivative.

Finding the value of 'b' by substituting the value of 'a' into the equation.

Using the first derivative equation to solve for 'c' with known values of 'a' and 'b'.

The original equation is revisited to find the value of 'd' with all other coefficients known.

Final determination of all coefficients 'a', 'b', 'c', and 'd' for the original equation.

The complete original function is expressed with the found coefficients.

Emphasis on the practical application of the method for solving equations with given points.

Highlighting the importance of systematic approach in solving complex derivative equations.

The transcript concludes with a summary of the steps taken to solve the original equation.

Transcripts

Browse More Related Video

Determine Cubic Equation Calculus grade 12

Determine Cubic Equation grade 12

Writing Quadratic Equations In Vertex Form & Standard Form Given 3 Points

Calculus Grade 12: Practice

Find and Classify all Critical Points of a Multivariable Function

Draw Cubic Graph Grade 12

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Bracket MethodDerivativesEquation SolvingMathematicsAlgebraEducational ContentLearning ToolProblem SolvingMath StrategyEducational Video