Introduction to Differential Equations (Differential Equations 2)

Professor Leonard
17 Sept 201809:56
EducationalLearning
32 Likes 10 Comments

TLDRThis introductory video on differential equations explains their purpose in modeling real-life changes through derivatives. It emphasizes the balance between creating accurate mathematical models and the complexity that comes with additional variables. The video outlines that differential equations involve derivatives and are about finding the function that a derivative belongs to. Solutions to these equations are families of equations with arbitrary constants, which can be narrowed down to specific solutions using initial conditions. The distinction between ordinary and partial differential equations is also briefly touched upon, setting the stage for further exploration in subsequent videos.

Takeaways
  • 📚 Differential equations are mathematical models used to represent real-life changes and situations.
  • 🔍 The primary goal is to find the function that a derivative in an equation represents, which is the solution to the differential equation.
  • ⚖️ There's a balance between creating a perfect model and the ability to solve it, which sometimes involves omitting certain aspects of the situation.
  • 📈 Derivatives are central to differential equations as they represent change, such as velocity, acceleration, or population growth.
  • 🧩 A solution to a differential equation is an equation itself and often belongs to a family of solutions with an arbitrary constant (+C).
  • 🔢 The order of a differential equation is determined by the highest derivative present, and it affects the number of arbitrary constants in the solution.
  • 🌐 Ordinary differential equations (ODEs) involve one independent variable, whereas partial differential equations (PDEs) involve multiple independent variables.
  • 📌 The process of solving a differential equation often starts with finding a general solution and then narrowing it down to a particular solution using initial conditions.
  • 🔄 The concept of 'plus C' (+C) is crucial as it represents the infinite family of solutions that can satisfy the differential equation.
  • 🔍 The next step in learning differential equations is to verify whether a given equation is indeed a solution to a differential equation.
  • 🎓 Understanding differential equations involves recognizing that they are a tool for modeling change and that solutions are typically functions rather than numerical values.
Q & A

  • What is the primary goal of studying differential equations?

    -The primary goal of studying differential equations is to model real-life situations or changes using mathematical models, particularly those involving rates of change or derivatives.

  • What is the balance that needs to be maintained when creating mathematical models for real-life situations?

    -The balance lies between creating a model that perfectly represents the situation and the ability to actually solve the mathematical model. Sometimes, aspects of the situation are omitted to make the math more manageable, even though it might not perfectly represent the real-life scenario.

  • What does a differential equation relate?

    -A differential equation relates a derivative within an equation. It is an equation that includes derivatives, representing systems with rates of change or variables that are changing over time.

  • How do derivatives represent change in the context of differential equations?

    -Derivatives represent quantities that are changing, such as velocity, acceleration, or population change with respect to time. Differential equations use these derivatives to model and analyze these changes mathematically.

  • What is the general form of a solution to a differential equation?

    -The general form of a solution to a differential equation is an equation itself, often involving an arbitrary constant (plus C), which represents a family of solutions that satisfy the differential equation.

  • How does the order of a differential equation affect the number of arbitrary constants in its solution?

    -The order of a differential equation, which is the highest derivative present in the equation, determines the number of arbitrary constants in its solution. For example, a first-order differential equation has one arbitrary constant, while a second-order differential equation has two, and so on.

  • How can an initial condition be used to narrow down a general solution to a particular solution?

    -An initial condition provides a specific point that the solution must pass through. By applying this condition to the general solution, which includes arbitrary constants, one can determine the specific values of these constants, thus narrowing down the general solution to a particular one that satisfies the given condition.

  • What is the difference between ordinary differential equations (ODEs) and partial differential equations (PDEs)?

    -Ordinary differential equations (ODEs) are based on a single independent variable, usually denoted as 'x' or 't' for time. In contrast, partial differential equations (PDEs) involve multiple independent variables and describe the relationships between the variables and their partial derivatives.

  • Why do we often find an infinite family of solutions when solving a differential equation?

    -We find an infinite family of solutions because the general solution to a differential equation typically includes arbitrary constants. These constants allow for a range of solutions that all satisfy the differential equation, forming a family of curves or functions.

  • What is the significance of the plus C in the context of integrals and differential equations?

    -The plus C in the context of integrals and differential equations signifies the arbitrary constant that is introduced when integrating. It represents the fact that there are infinitely many functions that could have been differentiated to produce the given differential equation, each differing by a constant.

  • How can we check if a given equation is a solution to a differential equation?

    -To check if an equation is a solution to a differential equation, we substitute the equation into the differential equation and verify if it satisfies the equation. If the left-hand side of the differential equation equals the right-hand side after the substitution, then the equation is indeed a solution.

Outlines
00:00
📚 Introduction to Differential Equations

This paragraph introduces the concept of differential equations, explaining their purpose in modeling real-life situations and changes. It emphasizes the balance between creating accurate mathematical models and the practicality of solving them. The paragraph outlines the goals of studying differential equations, which include understanding their basis in derivatives that represent change, and the process of refining mathematical techniques to better represent these models. It also touches on the idea that solutions to differential equations are equations themselves, often part of an infinite family characterized by an arbitrary constant (plus C), and how initial conditions can be used to narrow down to a particular solution.

05:01
🔢 Understanding the Order and Types of Differential Equations

This paragraph delves into the specifics of differential equations, discussing the order of a differential equation (based on the highest derivative present) and how it affects the number of arbitrary constants in the solution. It explains that with each increase in order, the number of constants increases, leading to a family of solutions. The paragraph also differentiates between ordinary differential equations (ODEs), which have one independent variable, and partial differential equations (PDEs), which involve multiple independent variables. The summary highlights the process of narrowing a general solution to a particular one using initial conditions and sets the stage for the next video, which will focus on checking whether an equation is a solution to a differential equation.

Mindmap
Keywords
💡Differential Equations
Differential equations are mathematical equations that involve an unknown function and its derivatives. They are used to model real-life situations that involve change, such as velocity, acceleration, or population growth over time. In the context of the video, differential equations are the central topic, with the goal of explaining how they represent change with math and how to identify and solve them.
💡Real-life Modeling
Real-life modeling refers to the process of creating mathematical models that represent and help understand real-world phenomena. In the video, it is emphasized that the primary goal of differential equations is to model real-life changes, such as the growth or decay of populations, or the motion of objects. This involves balancing the complexity of the model with the ability to perform the necessary calculations.
💡Derivatives
Derivatives are a fundamental concept in calculus, representing the rate of change of a function with respect to its variable. In differential equations, derivatives are used to describe how quantities change over time or in response to other variables. They are central to the definition of a differential equation, which involves an equation that includes derivatives.
💡Solutions
In the context of differential equations, a solution is a function that satisfies the equation. Unlike algebraic equations, the solutions to differential equations are typically other equations, often involving arbitrary constants. These solutions represent the infinite family of possible functions that could describe the behavior of the system being modeled.
💡Arbitrary Constants
Arbitrary constants are values that are added to the general solution of a differential equation to account for the unknown initial conditions of the problem. The number of arbitrary constants in a solution corresponds to the order of the differential equation—the higher the order, the more constants are needed.
💡Initial Conditions
Initial conditions are specific values assigned to the variables in a differential equation at the starting point in time. They are crucial for transforming a general solution into a particular solution that matches a specific scenario. By applying initial conditions, one can determine the unique values of the arbitrary constants in the solution.
💡Ordinary Differential Equations (ODEs)
Ordinary differential equations (ODEs) are a class of differential equations where there is only one independent variable. This contrasts with partial differential equations, which involve multiple independent variables. ODEs are the focus of the video, as they deal with situations where changes are primarily dependent on a single variable, such as time or position.
💡Partial Differential Equations (PDEs)
Partial differential equations (PDEs) are a type of differential equation that involves multiple independent variables. Unlike ordinary differential equations, which have only one independent variable, PDEs are used to model situations where changes depend on more than one variable, such as in the case of heat distribution across a surface or waves in a medium.
💡Integrals
Integrals are a mathematical operation that are used to find the area under a curve or to reverse the process of differentiation. In the context of differential equations, integrals are often used to find the general solution of a differential equation by integrating the equation to obtain the function that describes the behavior of the system.
💡Change
In the context of the video, change refers to the variations or alterations that occur in the quantities being modeled, such as the growth of a population or the fluctuation of a stock price. Differential equations are designed to capture and predict these changes by relating the rates of change (derivatives) to the underlying functions.
Highlights

Introduction to differential equations and their real-life applications.

Differential equations aim to model real-life changes and situations through mathematical models.

Balancing the complexity of a mathematical model with the ability to solve it is a key challenge.

Differential equations involve derivatives, which represent change, and are thus essential for modeling dynamic systems.

Solutions to differential equations are typically equations themselves, not just numbers.

The process of solving differential equations often involves finding an infinite family of solutions represented by 'plus C'.

The order of a differential equation, determined by the highest derivative present, affects the number of arbitrary constants in the solution.

Initial conditions are used to narrow down a general solution to a particular one.

Ordinary differential equations (ODEs) are based on a single independent variable, usually X or T for time.

Partial differential equations (PDEs) involve multiple independent variables and are a more complex type of differential equation.

The video aims to demystify differential equations and provide a foundation for further learning.

The importance of understanding the basics of derivatives and integrals in the context of differential equations is emphasized.

The video series will teach how to identify whether an equation is a solution to a differential equation.

The concept of 'plus C' and its significance in representing a family of solutions is discussed.

The role of arbitrary constants in solutions increases with the order of the differential equation.

The video provides a clear and accessible explanation of the fundamentals of differential equations, suitable for beginners.

Transcripts

Browse More Related Video

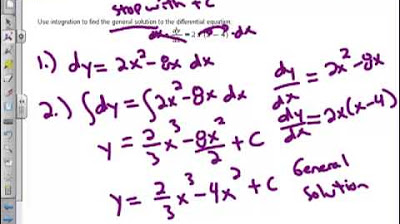
Differential Equations BC Calculus

Differential equation introduction | First order differential equations | Khan Academy

Separation of Variables

Lec 1 | MIT 18.03 Differential Equations, Spring 2006

Business Calculus - Math 1329 - Section 5.1 - Indefinite Integration & Differential Equations

What is a DIFFERENTIAL EQUATION?? **Intro to my full ODE course**

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Differential EquationsMath ModelingReal-Life ApplicationsDerivativesIntegralsPlus CSolutions as FunctionsOrdinary vs PartialEducational ContentMathematics Learning