Introduction to Slope Fields (Differential Equations 9)
TLDRThe transcript discusses the concept of slope fields in the context of differential equations, emphasizing their utility in approximating solutions when exact solutions are unattainable. It explains how first derivatives represent slopes and can be visualized across the XY plane to form a general solution, with a specific solution requiring an initial condition. The process of creating a slope field is detailed, highlighting the patterns and the method of plotting slopes at each point to construct an approximation of the solution's path. The transcript also touches on the trade-offs between the complexity of equations and our ability to solve them, suggesting that approximations are often practical and sufficient for real-world applications.
Takeaways
- 📚 Differential equations often require approximations when exact solutions are unattainable.
- 🌟 The concept of slope fields helps visualize the general solution of a differential equation without needing an exact formula.
- 📈 Slope fields are created by calculating the slope (first derivative) at every point in the xy-plane, representing the instantaneous rate of change.
- 🔍 To create a slope field, one must find the slope (X + Y) for each point on the xy-plane and plot a line representing that slope.
- 📊 A general solution is represented by the collection of all possible slopes across the xy-plane, indicating all potential curves that satisfy the differential equation.
- 🎯 To find a particular solution, one must start with an initial condition (a specific point) and draw a curve that fits the slopes of the slope field through that point.
- 🤔 Even when a differential equation appears unsolvable, slope fields provide a method to approximate solutions and understand the behavior of the function.
- 🧠 The process of creating a slope field involves identifying patterns in the slopes to efficiently plot the field without a calculator.
- 🛠️ Real-life applications often rely on these approximations, as not all differential equations can be solved exactly but can still be modeled effectively.
- 🔧 The trade-off in modeling is between accuracy and solvability; perfect representation may not be solvable, while solvable models may lack precision.
- 📝 Practice is essential to understanding slope fields, starting with simple examples by hand and progressing to more complex equations using computational tools.
Q & A
What is the main topic of the video?
-The main topic of the video is the concept of slope fields in the context of differential equations, and how they can be used to approximate solutions even when an exact solution cannot be found.
Why might we not always have an exact solution for a differential equation?
-In real-life scenarios, it's not always possible to have an exact solution because some differential equations do not have good techniques for finding an exact general solution or even a particular solution. This is where approximations come into play.
What is a slope field?
-A slope field is a graphical representation that uses lines to depict the slope of a function at various points in the xy-plane. It is derived from the first derivative of a differential equation and helps visualize the direction and rate of change of potential solutions.
How does a slope field help in solving differential equations?
-A slope field provides a visual representation of the slopes (rates of change) at different points in the xy-plane. By following these slopes, one can approximate the path of a solution curve, especially when an exact solution is not feasible to find using standard techniques.
What is the significance of the first derivative in the context of slope fields?
-The first derivative of a function with respect to another variable represents the slope of the function at any given point. In slope fields, this derivative is used to calculate the slopes at various points in the xy-plane, which are then depicted as lines to form the slope field.
What is the difference between a general solution and a particular solution in the context of differential equations?
-A general solution represents all possible solutions to a differential equation, including all curves that fit the given slopes at every point. A particular solution, on the other hand, is a specific curve that not only fits the slopes but also passes through a given initial condition point.
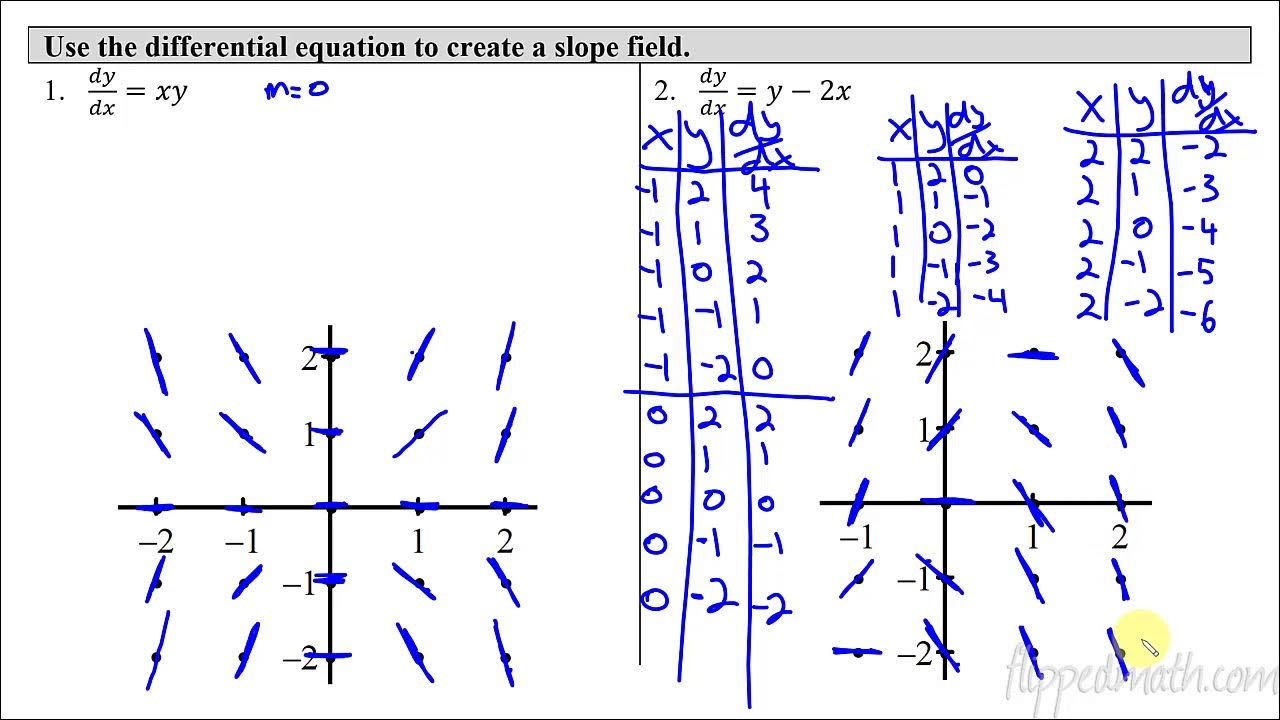
How do you create a slope field for a given differential equation?
-To create a slope field, you first find the first derivative of the differential equation, which represents the slopes. Then, you calculate these slopes for various points in the xy-plane and plot lines at each point to represent the direction and magnitude of the slope. This process results in a visual representation of all potential solution paths.
What is an example of a differential equation that might be difficult to solve but can be represented using a slope field?
-An example given in the transcript is the differential equation x^2 + 2y^2. This equation might not have a straightforward technique for finding an exact solution, but a slope field can be created to approximate solutions.
How does the concept of approximations relate to solving differential equations?
-Approximations are used when exact solutions cannot be found or are too complex to compute. By creating a slope field, one can approximate the solution path by following the slopes at various points, which provides a practical way to model and understand the behavior of the system described by the differential equation, even without an exact solution.
What is the trade-off mentioned in the video regarding the complexity of equations and their solvability?
-The trade-off discussed is that by limiting variables to make an equation more solvable, you might not perfectly represent the real-life situation you're modeling. Conversely, if you aim to perfectly represent a complex situation, you might not be able to solve the resulting equation. This highlights the balance between the need for accuracy and the ability to find solutions.
Outlines
📚 Introduction to Slope Fields
The video begins with an introduction to slope fields, emphasizing that while differential equations may not always have exact solutions, approximations can be used. The concept of slope fields is introduced as a way to visualize the slopes of a function at different points, which can help in understanding and approximating solutions to differential equations.
📈 Derivatives and Slopes
The second paragraph delves into the relationship between derivatives and slopes, explaining that the first derivative of a function represents the slope at any given point. The video aims to show how, by understanding this relationship, one can create a slope field that visually represents the slopes across the entire function, providing a method to approximate solutions.
🔍 Creating a Slope Field
This paragraph explains the process of creating a slope field by calculating the slope at various points on the XY plane. It describes how to plot these slopes as lines on a graph, which collectively form the slope field. The video emphasizes the importance of understanding this process to grasp the concept of slope fields and their role in approximating solutions to differential equations.
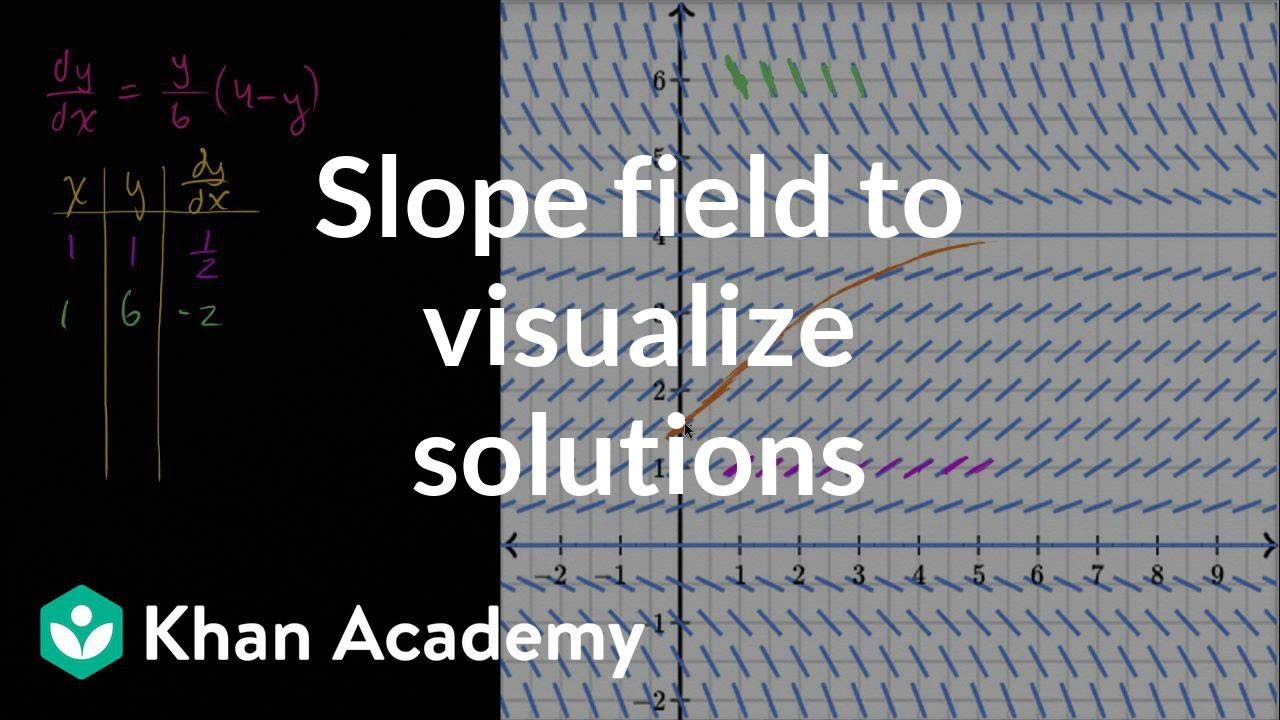
🌐 Visualizing General and Particular Solutions
The fourth paragraph discusses the difference between a general solution and a particular solution within the context of slope fields. It explains that a general solution is represented by the entire slope field, showing all possible slopes at every point, while a particular solution is a specific path through the field that fits a given initial condition.
📊 Examples of Slope Fields
The fifth paragraph provides examples of how to create slope fields for specific differential equations. It walks through the process of calculating slopes for different points and plotting them on the XY plane. The video uses these examples to illustrate how the slope field can be used to approximate the path of a particular solution through the field.
🎯 Applying Slope Fields to Real-Life
The final paragraph wraps up the discussion on slope fields by highlighting their practical applications. It suggests that while the examples provided are theoretical, the concepts can be applied to real-world problems. The video concludes by encouraging viewers to practice creating slope fields and to look forward to future videos where these concepts will be applied to real-life scenarios.
Mindmap
Keywords
💡Differential Equations
💡Solutions
💡Slope Fields
💡First Derivative
💡Approximations
💡General Solution
💡Particular Solution
💡XY-Plane
💡Rate of Change
Highlights
Exploring the concept of differential equations and their solutions.
Introducing the idea of slope fields as an alternative to exact solutions.
Discussing the practical use of approximations in solving real-life problems.
Describing the process of creating a slope field from a differential equation.
Explaining how first derivatives represent slopes and can be used to build a slope field.
Illustrating the method of finding slopes at specific points on the XY plane.
Discussing the concept of a general solution represented by a slope field.
Demonstrating how to approximate a particular solution using a slope field.
Showing the importance of initial conditions in finding a particular solution.
Providing examples of how to create a slope field by hand.
Highlighting the role of patterns in simplifying the process of creating a slope field.
Explaining the visual representation of slopes on an XY plane as unit vectors.
Describing the transition from a general solution to a particular solution through an initial point.
Discussing the concept of asymptotes in the context of slope fields.
Encouraging the use of technology for creating slope fields in more complex scenarios.
Providing a comprehensive understanding of slope fields and their applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: