Euler's method | Differential equations| AP Calculus BC | Khan Academy
TLDRThe video script introduces Euler's Method, a numerical technique for approximating solutions to differential equations that often cannot be solved analytically. It explains the process through a step-by-step example, starting with an initial condition and using the differential equation to estimate subsequent points. The method involves assuming a constant slope (derivative) over small intervals and adjusting the Y-value based on this slope. The accuracy of the approximation improves with smaller steps (delta X), demonstrating the power of numerical methods in simulating solutions to complex problems.
Takeaways
- 📚 Differential equations are mathematical models that describe various phenomena, but many are not easily solvable analytically.
- 🔢 The script introduces a specific differential equation: dY/dx = Y, with the initial condition Y(0) = 1, and its analytical solution Y = e^x.
- 💻 When analytical solutions are not feasible, numerical methods can be employed to approximate solutions using computers.
- 📈 The concept of a slope field is mentioned, which visually represents the slopes of the tangent lines for a differential equation at various points in the xy-plane.
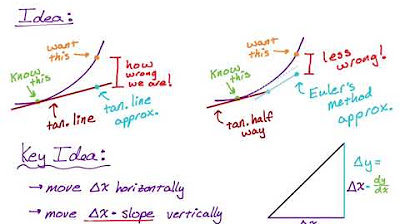
- 📍 Euler's Method is a numerical technique used to approximate solutions to first-order differential equations, demonstrated in the script.
- 🔄 Euler's Method involves making assumptions about the constancy of the derivative (slope) over small intervals in the x-axis.
- 🚶♂️ The process starts with an initial point and iteratively estimates the next point by using the current derivative (slope) to find the new y-value.
- 📉 The accuracy of the approximation can be improved by decreasing the size of the step (delta X) used in the iteration.
- 🌐 Euler's Method can be applied to a wide range of differential equations, not just the one discussed in the script.
- 🎯 The script highlights the practicality of Euler's Method as a tool for solving differential equations when exact analytical solutions are not possible.
- 🌟 The method is named after Leonhard Euler, a prominent mathematician known for his extensive contributions to the field of mathematics.
Q & A
What is the differential equation discussed in the script?
-The differential equation discussed is dY/dx = Y, with the initial condition Y(0) = 1.
What is the particular solution of the given differential equation?
-The particular solution is Y = e^x.
Why are many differential equations difficult to solve analytically?
-Many differential equations are complex and cannot be solved using traditional analytic methods due to their nature, making numerical methods necessary for approximations.
What is the role of computers in solving differential equations?
-Computers are essential for applying numerical methods to approximate and visualize the solutions of differential equations that cannot be solved analytically.
How does one set up a table for numerical approximation of a differential equation?
-One sets up a table with columns for X, Y, DY/DX, and DX, and uses the differential equation to calculate the slope (DY/DX) at each point.
What is Euler's Method and how does it relate to the script's content?
-Euler's Method is a numerical technique for approximating solutions to ordinary differential equations. It is the method demonstrated in the script for approximating the solution to dY/dx = Y with the initial condition Y(0) = 1.
How does the step size (delta X) affect the accuracy of the approximation in Euler's Method?
-A smaller step size (delta X) results in a more accurate approximation because it captures more details of the slope changes over smaller intervals.
What is the significance of the slope field in understanding differential equations?
-A slope field is a visual representation of the slopes (DY/DX) at various points (X, Y) in the plane, which helps in understanding the behavior of the solutions to the differential equation.
How does the derivative relate to the slope of the tangent line in the context of the script?
-In the given differential equation, the derivative of Y with respect to X is equal to Y itself, which means the slope of the tangent line at any point is equal to the Y value at that point.
What is the process of Euler's Method for approximating the solution to a differential equation?
-Euler's Method involves starting with an initial condition, calculating the slope (derivative) at that point, and then incrementing X and Y according to the calculated slope over a specified interval (delta X) to approximate the next point on the solution curve.
How can one improve the approximation of e using Euler's Method for the given differential equation?
-By using smaller step sizes (delta X) and iterating the process of Euler's Method multiple times, one can improve the approximation of e by getting closer to the actual exponential growth pattern of the solution e^x.
Outlines
📚 Introduction to Differential Equations and Numerical Methods
This paragraph introduces the concept of differential equations, specifically focusing on a separable differential equation where the derivative of Y with respect to X is equal to Y. It explains the initial condition Y(0) = 1 and the particular solution Y(X) = e^X. The voiceover emphasizes the complexity of solving most differential equations analytically and introduces the concept of numerical methods as a powerful alternative, using computers to approximate solutions. The paragraph sets the stage for explaining a straightforward numerical method by drawing a table to illustrate the process of creating a slope field and approximating the solution from the initial condition.
🔍 Euler's Method: A Numerical Approach to Solving Differential Equations
This paragraph delves into Euler's Method, a numerical technique for approximating solutions to first-order differential equations. It describes the process of incrementing X values and using the derivative (slope) to estimate the corresponding Y values. The explanation includes a step-by-step demonstration of how to apply Euler's Method, starting from the initial condition and using a step size (delta X) to iteratively find new Y values. The paragraph highlights the impact of choosing different step sizes on the accuracy of the approximation, showing that smaller step sizes lead to more precise results. It concludes by reiterating the practicality of Euler's Method for solving differential equations that cannot be solved analytically.
Mindmap
Keywords
💡differential equation
💡separable differential equation
💡numerical methods
💡Euler's Method
💡initial condition
💡slope field
💡derivative
💡approximation
💡step size
💡analytic methods
💡computers
Highlights
The differential equation discussed is a separable one, where the derivative of Y with respect to X is equal to Y.
The particular solution to the differential equation with initial condition Y(0) = 1 is Y(X) = e^X.
Many differential equations are difficult or impossible to solve using analytic methods.
Numerical methods are effective for approximating solutions to differential equations, especially when analytic solutions are not feasible.
A table can be set up to create a slope field, which helps visualize the slopes at different points in the XY plane.
The derivative at any point for the given differential equation is equal to the Y value at that point.
Euler's Method is introduced as a straightforward numerical method for approximating solutions to differential equations.
The method starts with an initial condition and uses the derivative to estimate the next Y value based on a change in X.
The approximation can be improved by using smaller increments in X (delta X).
The transcript provides a step-by-step example of how Euler's Method can be applied to approximate the solution to the differential equation.
Euler's Method can be used to approximate the value of e (Euler's number) with increasing precision.
The transcript emphasizes that most real-world differential equations are solved or simulated using numerical methods like Euler's Method.
The transcript explains that the smaller the step size in Euler's Method, the closer the approximation will be to the actual solution.
The process of Euler's Method involves assuming a constant slope over an interval and then updating the slope based on the new Y value.
The transcript demonstrates that Euler's Method is a practical tool for solving differential equations that cannot be solved analytically.
The transcript provides a visual explanation of how the slope changes as X increases, using the example of the differential equation at hand.
The transcript concludes by highlighting the importance and application of numerical methods like Euler's Method in the study and solution of differential equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: