Problem Solving with Velocity and Acceleration (Differential Equations 8)
TLDRThe video script presents a comprehensive walkthrough of solving various word problems involving differential equations, with a focus on integration as the primary technique. The examples range from basic to advanced, covering scenarios like projectile motion, free fall, and braking distances. The key concepts discussed include understanding acceleration, initial velocity, and position functions, as well as how to apply these to real-world physics problems. The script emphasizes the importance of unit consistency and logical inference when dealing with such mathematical problems.
Takeaways
- 📚 Start by understanding the basic concepts of differential equations and integration as they apply to physical problems.
- 🔢 When solving problems, it's crucial to identify and use the correct units and constants, such as the acceleration due to gravity on Earth.
- 🎯 Initially, infer as much information as possible from the problem statement, including the planet's gravity, initial velocities, and positions.
- 🌐 For problems involving motion, use the relationship between acceleration, velocity, and position to build equations and solve for unknowns.
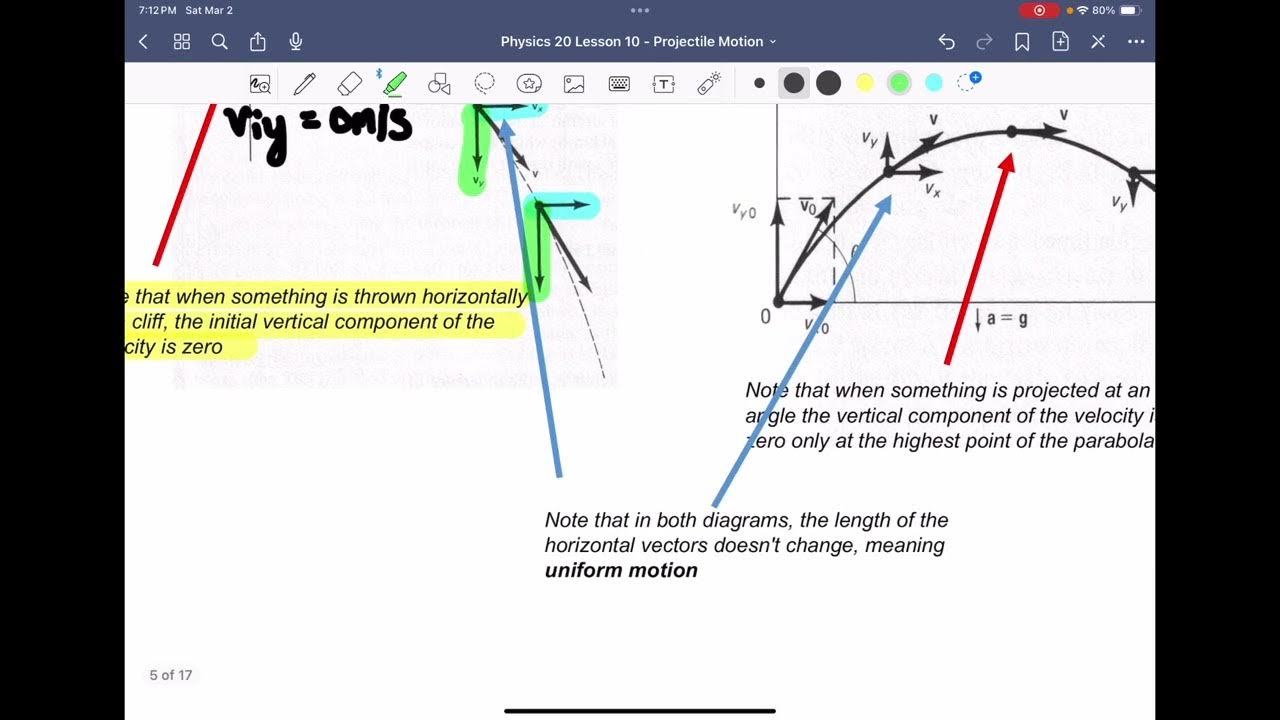
- 🚀 To find the maximum height in a projectile motion problem, set the velocity equation to zero to determine the time at which the object reaches its peak height.
- 📉 When dealing with free-fall or dropping objects, integrate the acceleration to find the velocity function and then again to find the position function.
- 🕒 The time it takes for an object to hit the ground can be found by setting the final position to zero and solving the position equation.
- 🛣️ In braking problems, determine the deceleration by using the initial velocity, the distance skidded, and the time it takes to stop.
- 🌟 For problems set on different planets, use the known acceleration on Earth to calculate the initial velocity, then adjust for the alien planet's gravity.
- 🔄 When the acceleration is not given, work backwards from the position function to find the time and velocity at the point of interest.
- 📈 Practice is key in mastering these types of problems; approach them systematically and methodically to build confidence and skill.
Q & A
What is the basic technique used to solve differential equations in the examples provided?
-The basic technique used to solve the differential equations in the examples is integration.
What is the significance of the acceleration value in the context of the slingshot example?
-The acceleration value, which is negative 9.8 meters per second squared on Earth, represents the constant acceleration due to gravity acting on the projectile fired from the slingshot.
How does the initial velocity of the projectile affect the maximum height it reaches?
-The initial velocity of the projectile determines how high it will go before gravity causes it to start descending. A higher initial velocity will generally result in a greater maximum height.
What is the role of the constant 'C' in the equations derived from the examples?
-The constant 'C' in the equations represents an arbitrary constant that arises from integration. It is determined by the initial conditions of the problem, such as the initial velocity or position.
Why is it important to match units when solving problems involving physical quantities?
-Matching units is crucial to ensure the correctness of calculations and the physical relevance of the results. It allows for accurate comparisons and conversions between different quantities.
How does the time it takes for an object to hit the ground relate to its initial velocity and acceleration in free fall problems?
-The time it takes for an object to hit the ground in a free fall problem can be determined by setting the velocity equation to zero (since velocity is zero at the ground) and solving for time using the initial velocity and acceleration due to gravity.
What is the maximum height reached by a projectile launched with an initial velocity of 49 meters per second on Earth?
-The maximum height reached is approximately 120.25 meters, calculated by integrating the velocity function twice and evaluating the position function at the time when the velocity is zero.
How does the concept of maximum height and time to hit the ground apply to the example of a car braking?
-In the car braking example, the maximum height concept is not applicable as the car is not launched into the air. Instead, the focus is on the time it takes for the car to come to a stop from a certain initial velocity, given a constant deceleration.
What is the significance of the initial position in solving these types of problems?
-The initial position is a crucial piece of information that allows us to determine the constant terms in the velocity and position functions derived from the integration of the acceleration function. It sets the starting point for the motion being analyzed.
How does the example of a brick being dropped from a height illustrate the use of differential equations?
-The example of a brick being dropped from a height demonstrates how differential equations can model real-world physical situations. By integrating the acceleration function, we find the velocity function, and integrating once more gives us the position function. The time when the position is zero (ground level) can then be found by solving the velocity function for zero velocity.
Outlines
📚 Introduction to Solving Differential Equations
The speaker introduces the topic of differential equations, emphasizing the importance of understanding the basic technique of integration to solve them. They announce a series of ten examples to practice, ranging from easy to difficult, and encourage the audience to stick with the examples to improve their understanding and problem-solving approach.
🚀 Slingshot Projectile Motion
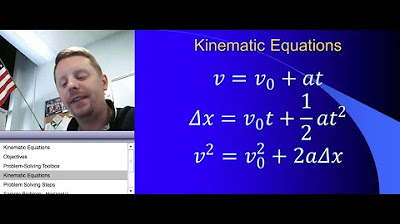
The speaker presents a problem involving a slingshot shooting a projectile upward with an initial velocity of 49 meters per second. They explain the need to consider Earth's gravity (negative 9.8 meters per second squared) and walk through the process of finding the maximum height reached by the projectile using integration of acceleration to find velocity and position functions.
🧱 Dropping a Brick from a Height
The speaker discusses the scenario of dropping a brick from a height of 400 feet and uses the constant acceleration due to gravity to find out when and at what speed the brick will hit the ground. They detail the steps of integrating the acceleration to find the velocity function and then the position function, ultimately solving for the time and speed at impact.
🚗 Car Braking Distance
The speaker explains how to calculate the distance a car will travel when braking from 100 kilometers per hour (or 60 miles per hour) at a constant deceleration of ten meters per second squared. They highlight the importance of unit consistency and provide a step-by-step solution to find out when the car stops and how far it travels during braking.
🎾 Velocity and Position of a Moving Car
The speaker continues with the car braking scenario, focusing on the velocity and position functions to determine the distance traveled by the car before it stops. They integrate the velocity function to find the position function and use the time when the velocity is zero to calculate the distance, emphasizing the practical importance of such calculations.
🏢 Maximum Height of a Building
The speaker presents a problem involving shooting a paintball from the top of a building and calculating the building's height based on the time it takes for the paintball to hit the ground after being shot upward at a certain velocity. They outline the process of finding the maximum height by setting the velocity to zero and solving for the time, then using that time to find the position function.
🍉 Throwing a Watermelon from a Building
The speaker discusses a hypothetical scenario of throwing a watermelon from the top of a building and using the information about its final velocity and the time it takes to hit the ground to determine the height of the building. They explain the steps of calculating the time to achieve a certain velocity and then using that to solve for the initial position, which in this case is the height of the building.
🚛 Deceleration and Braking Time
The speaker introduces a problem involving a truck traveling at 60 miles per hour that begins to slide or skid due to deceleration. The challenge is to find out the deceleration rate and the time it takes for the truck to stop, given that it skids a total of 176 feet. The speaker outlines the process of using integration and the known distances and velocities to solve for the unknowns.
🌍 Comparing Gravity on Different Planets
The speaker discusses the concept of comparing the gravitational pull of different planets by using the known acceleration due to gravity on Earth to calculate the initial velocity needed to throw a rock a certain distance on another planet with different gravity. They explain how to use the position function and the time it takes to reach maximum height to find the required initial velocity.
🚀 Calculating Maximum Height on Another Planet
The speaker concludes with a problem of calculating the maximum height a rock could be thrown on a planet with a known gravitational pull. They demonstrate how to use the initial velocity found from Earth's gravity to determine the time and height of the rock when thrown on the other planet, emphasizing the importance of understanding the formulas and applying them to different scenarios.
Mindmap
Keywords
💡Differential Equations
💡Integration
💡Initial Velocity
💡Acceleration
💡Position Function
💡Velocity Function
💡Critical Points
💡Arbitrary Constant
💡Deceleration
💡Maximum Height
Highlights
The discussion begins with an introduction to solving differential equations using integration as the fundamental technique.
The first example involves calculating the maximum height reached by a projectile launched with an initial velocity of 49 meters per second on Earth.
The importance of understanding the context, such as the planet Earth and its gravitational acceleration, is emphasized for solving problems accurately.
The process of finding the maximum height involves integrating the acceleration to find the velocity function and then using the velocity function to find the position function.
The concept of critical points, where the first derivative (velocity) equals zero, is used to find the maximum height of the projectile.
The second example is about calculating the time and speed at which a brick dropped from a height of 400 feet will hit the ground.
The method involves using the constant acceleration due to gravity and integrating it to find the velocity and position functions.
The time it takes for the brick to hit the ground is found by setting the position function equal to zero and solving for time.
The third example discusses a car traveling at 100 kilometers per hour (60 miles per hour) and its distance traveled before stopping due to constant deceleration.
Unit conversion from kilometers per hour to meters per second is necessary to match the units of acceleration.
The car's deceleration is assumed to be constant, and the velocity function is used to find the time it takes to stop by setting velocity to zero.
The position function is then used to calculate the distance traveled before the car stops by plugging in the time found in the previous step.
The fourth example involves a paintball shot from a 20-meter high building with an initial velocity of 300 meters per second.
The maximum height of the paintball is determined by finding the time when the velocity becomes zero, indicating the peak of its trajectory.
The time it takes for the paintball to hit the top of the building and the ground is calculated by setting the position function equal to the building's height and solving for time.
The process involves integrating the acceleration to find the velocity function and then integrating the velocity function to find the position function.
The final example in the transcript discusses throwing a watermelon from the top of a building with an initial velocity of 10 meters per second downwards.
The problem involves finding the height of the building by using the time it takes for the watermelon to reach the ground and the final velocity.
The height of the building is determined by solving for the initial position using the position function and the time it takes for the watermelon to hit the ground.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: