Slope Fields | Calculus
TLDRThis video tutorial explains the concept of slope fields and their application in differential equations. It begins with a basic understanding of slopes and their graphical representation, such as horizontal lines for a slope of zero and diagonal lines for positive and negative slopes. The video then progresses to illustrate how to plot slope fields for given differential equations, using examples like y'=x and y'=y. It also demonstrates how to match a graphical representation of a slope field to its corresponding differential equation. The tutorial concludes with solving the equations, showing that the solutions can take shapes like parabolas or circles, depending on the equation. The video is an informative guide for those interested in visualizing and solving differential equations through slope fields.
Takeaways
- 📈 Understanding slopes is crucial for drawing slope fields, with a slope of 0 representing a horizontal line, positive slopes indicating upward angles, and negative slopes indicating downward angles.
- 🌐 For the differential equation y' = x, the slope field can be plotted by recognizing that y' depends only on x, leading to a parabolic solution curve.
- 🔄 When solving y' = y, the slope field reveals an exponential shape, and the solution can be expressed as y = c * e^x, confirming the slope field's indicative nature.
- 🔢 For the more complex equation y' = x - y, identifying patterns in the slope field is essential for accurate graphing, and the solution is a linear equation y = x - 1.
- 🔍 The process of matching a given slope field graph to the correct differential equation involves testing individual points for consistency with each equation's slope.
- 📊 The general solution x^2 + y^2 = c represents the equation of a circle, with the constant c determining the circle's size.
- 🎥 The video script serves as an educational guide on how to draw slope fields, interpret their characteristics, and solve corresponding differential equations.
- 🌟 Recognizing the shapes that emerge from the slope field, such as parabolas, exponentials, and circles, is key to identifying the correct form of the differential equation.
- 🛠️ The slope field is a visual tool that not only helps in graphing but also provides insights into the nature of the solutions to differential equations.
- 📚 The script emphasizes the importance of practice problems in solidifying the understanding of slope fields and their relationship to differential equations.
- 🔗 The video also references additional resources, such as another video on first-order linear differential equations, for further learning and understanding.
Q & A
What does a slope of zero represent in the context of the video?
-A slope of zero represents a horizontal line.
What is the significance of a slope of one in the video?
-A slope of one signifies a line that goes up at a 45-degree angle.
How does a negative slope affect the direction of the line?
-A negative slope indicates that the line goes down, with the angle increasing as the absolute value of the slope increases.
What happens when the slope is a very large number or undefined?
-When the slope is a very large number or undefined, the line is vertical.
How does the video demonstrate the process of drawing a slope field?
-The video demonstrates drawing a slope field by starting with a table of x, y, and y prime values, then plotting lines with slopes corresponding to the y prime values at different x points.
What is the general solution to the differential equation y prime equals x?
-The general solution to the differential equation y prime equals x is y equals one-half x squared plus a constant (c).
How does the slope field help in understanding the shape of the solution to a differential equation?
-The slope field provides a visual representation of the slopes at various points, which gives a good idea of the shape of the solution curve to the differential equation.
What is the differential equation for the second example in the video?
-The differential equation for the second example is y prime equals y.
What type of function does the solution to the second differential equation resemble?
-The solution to the second differential equation resembles an exponential function.
How does the video explain the process of solving the third differential equation, y prime equals x minus y?
-The video explains that the third differential equation, y prime equals x minus y, can be put into standard form as y prime plus y equals x, and then refers to another video for the solution method.
What is the general solution to the differential equation y prime plus y equals x?
-The general solution to the differential equation y prime plus y equals x is y equals x minus one plus a constant (c).
How does the video relate the shape of the graph to the equation x squared plus y squared equals c?
-The video relates the shape of the graph to the equation x squared plus y squared equals c by showing that the graph has the shape of a circle, with c representing the square of the radius of the circle.
Outlines
📈 Introduction to Slope Fields and Differential Equations
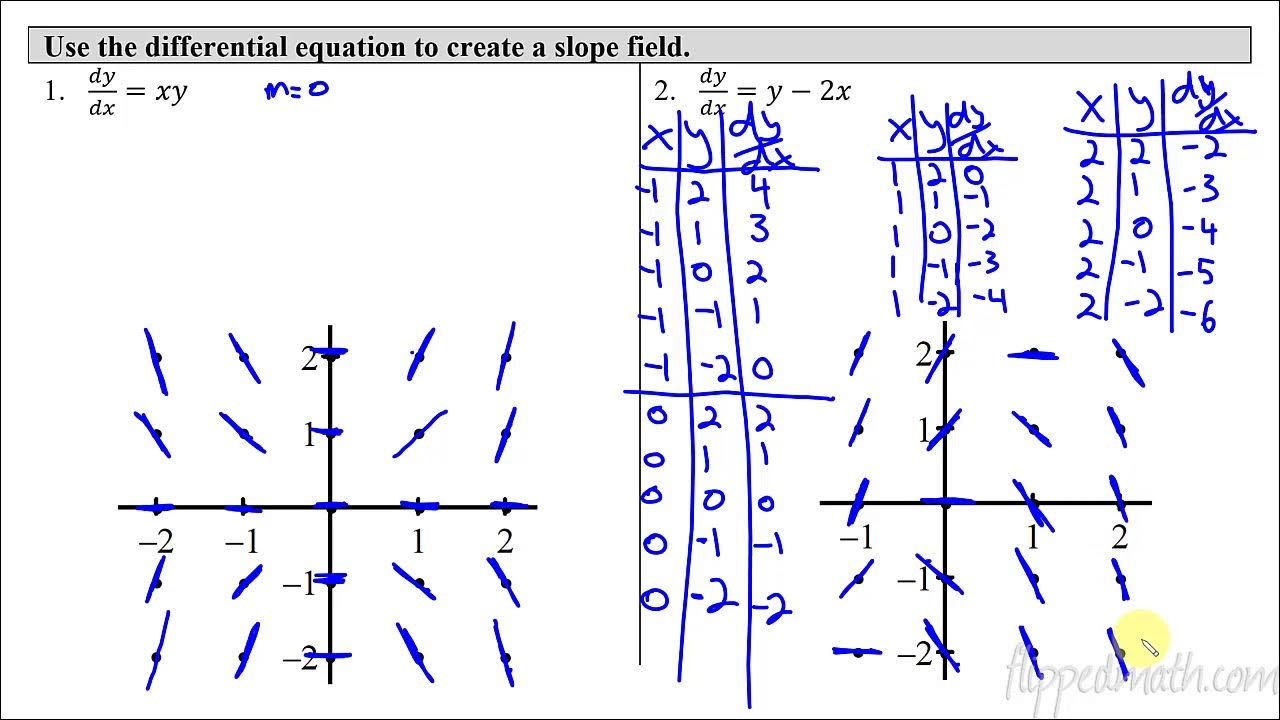
This paragraph introduces the concept of slope fields and their relation to differential equations. It explains the meaning of different slopes (e.g., 0 for horizontal lines, positive and negative values for angles of inclination) and emphasizes the importance of understanding slopes when drawing slope fields. The paragraph also presents a practice problem involving the differential equation y' = x, guiding through the process of creating a table for x, y, and y' values, and drawing the corresponding slope field. It concludes with the observation that the general solution to this equation has a parabolic shape.
🧮 Solving Differential Equations with y' = y
The second paragraph focuses on solving a differential equation where y' is equal to y. It describes how to plot the slope field by creating a table and determining the slope based on the value of y. The paragraph explains that the solution to this equation appears exponential and proceeds to solve the equation by separating variables and finding anti-derivatives, resulting in a solution of the form y = c * e^(x). The summary highlights the process of identifying the shape of the solution (exponential) through the slope field and confirms the solution by comparing it to the general shape of exponential functions.
📊 Graphing y' = x - y and Identifying Patterns
This paragraph discusses a more complex differential equation where y' depends on both x and y. It outlines the process of graphing the slope field by identifying patterns in the slopes at various points (e.g., when x and y are equal, the slope is zero). The paragraph then describes how to extend these patterns to other points and how to estimate the shape of the solution based on the slope field. It also provides a brief mention of a video on solving first-order linear differential equations and presents the solution y = x - 1, verifying it against the differential equation.
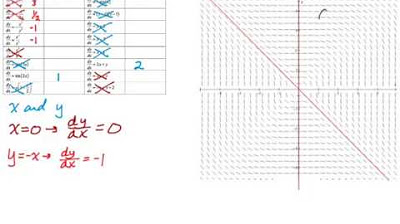
🔍 Matching Slope Fields to Differential Equations
The fourth paragraph presents a multiple-choice problem where the slope field graph must be matched to the correct differential equation. It explains the process of selecting a point on the graph and checking which equation's slope matches that point. The paragraph eliminates incorrect choices based on the slope at the selected point and identifies the correct equation y = -x/(x^2 + y^2). It then solves the differential equation by integrating both sides, resulting in the general solution x^2 + y^2 = 2c, which is recognized as the equation of a circle with a radius of √2.
🎓 Conclusion and Overview of Slope Fields
The final paragraph concludes the video by summarizing the key points discussed. It reiterates the process of graphing slope fields and matching them to the appropriate differential equations. The paragraph also highlights the importance of understanding the general shape of the solution (e.g., parabolic, exponential, circular) and how this shape can be deduced from the slope field. The video ends with a thank you note to the viewers for their attention and participation.
Mindmap
Keywords
💡Slope Field
💡Differential Equation
💡Slope
💡Horizontal Line
💡Parabolic Shape
💡Exponential Function
💡Linear Equation
💡Circle
💡Antiderivative
💡Separation of Variables
💡First Derivative
Highlights
The video discusses how to draw a slope field and match it with the appropriate differential equation.
A slope of 0 represents a horizontal line.
A slope of one corresponds to a line going up at a 45-degree angle.
A negative slope indicates a line going down, with the angle's magnitude representing the steepness.
A very large or undefined slope results in a vertical line.
The practice problem involves the differential equation y' = x.
The slope field for y' = x is plotted by creating a table of x, y, and y' values.
The general solution to y' = x has a parabolic shape.
The differential equation y' = y is solved by separating variables and integrating.
The solution to y' = y is an exponential function with the general shape of an exponential curve.
For the equation y' = x - y, the slope field is harder to graph because y' depends on two variables.
The slope field for y' = x - y reveals patterns that help in plotting the field quickly.
One solution to the equation y' = x - y is a linear equation y = x - 1.
The video provides a method to verify the solution to a differential equation by plugging in values.
The slope field for the equation y' = -x/y reveals a circular shape.
The general solution to the equation y' = -x/y is x^2 + y^2 = c, which is the equation of a circle.
The video demonstrates how to match a given slope field graph to the correct differential equation by testing points.
The video concludes by emphasizing the introduction to slope fields, their graphing, and matching them to equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: