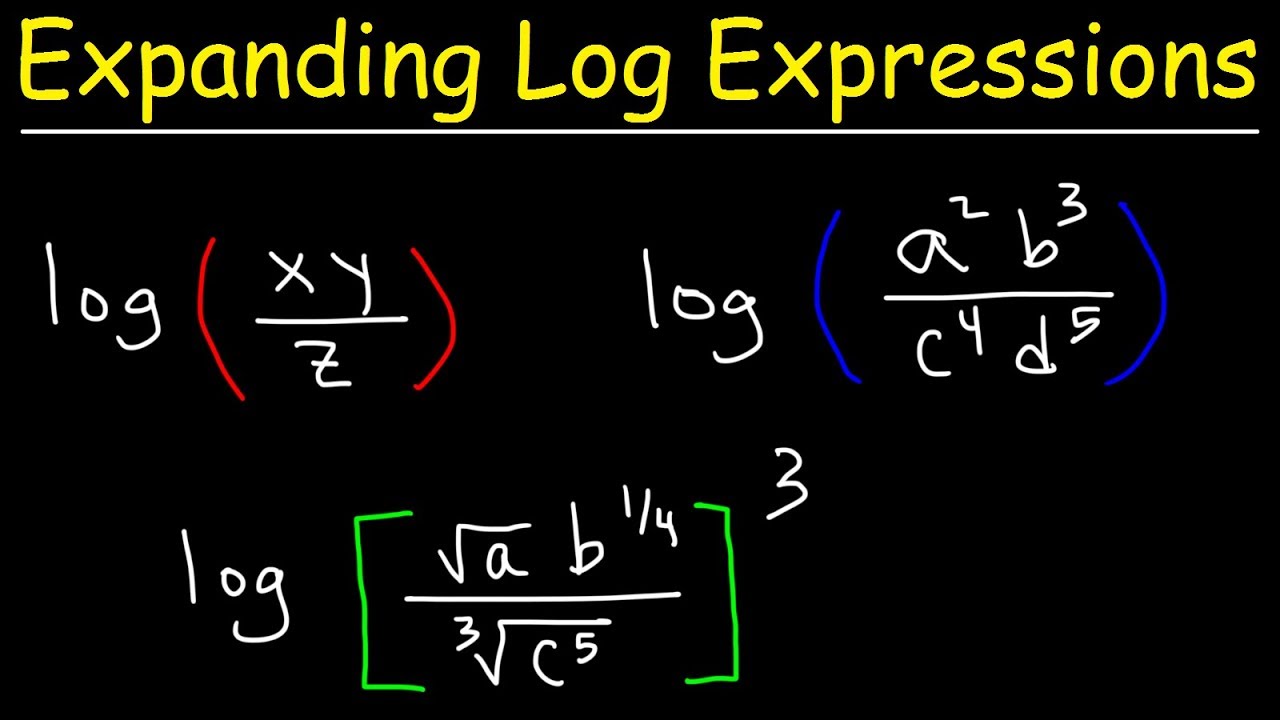
Condensing Logarithmic Expressions
TLDRThis educational video lesson focuses on condensing multiple logarithms into a single logarithmic expression. It begins by demonstrating the process with a simple example, combining log a, log c, and -log b into log(ac/b). The lesson then progresses to more complex examples, showing how to move coefficients to the exponent position and combine them accordingly. It illustrates this with expressions like 2 log a + 5 log b - 7 log c, which is simplified to log(a^2 * b^5 / c^7). The video also covers expressions with fractional coefficients, such as (1/3)log a - (2/3)log b + (1/4)log c - (4/5)log d, and demonstrates how to rewrite them as a single logarithm or in radical form. The lesson is a practical guide for students looking to master the manipulation of logarithmic expressions.
Takeaways
- 📚 The lesson focuses on condensing multiple logarithms into a single logarithm, which is the reverse process of the previous lesson.
- 🔍 To combine logs, positive coefficients are placed in the numerator and negative coefficients in the denominator.
- 📈 The first example shows combining logs by placing \( \log(ac) \) over \( \log(b) \), where 'a' and 'c' have positive signs and 'b' has a negative sign.
- 🔢 In the second example, coefficients are moved to the exponent position, resulting in \( \log(a^2) + \log(b^5) - \log(c^7) \).
- 📉 The second example's final form is \( \log(\frac{a^2b^5}{c^7}) \), showing how to write a single log with positive and negative terms.
- 🧩 The third example involves fractional coefficients, which are first converted to exponents before combining into a single logarithm.
- 📊 The third example's final form is \( \log(\frac{a^{1/3}c^{1/4}}{b^{2/3}d^{4/5}}) \), demonstrating the process with fractional exponents.
- 📌 The lesson emphasizes the importance of correctly identifying the sign in front of each term to determine its position in the combined logarithm.
- 📘 The process involves converting coefficients to exponents, which is a key step in combining multiple logarithms into one.
- 📙 An alternative representation of the combined logarithm is provided, using radical forms such as cube roots and fourth roots.
- 📒 The lesson concludes with the ability to express a combined logarithm in both logarithmic and radical forms, offering flexibility in mathematical expression.
Q & A
What is the main topic of this lesson?
-The main topic of this lesson is to condense multiple logarithms into a single logarithm, which is the opposite of the previous lesson on expanding a single logarithm into multiple logarithms.
Why is it important to have watched the previous lesson before this one?
-It is important to have watched the previous lesson because this lesson builds upon the concepts taught there, specifically the expansion of a single logarithm into multiple logarithms, and now it's focusing on the reverse process.
How is the first example in the transcript simplified into a single logarithm?
-The first example is simplified by combining the terms with positive signs (a and c) on top and the term with a negative sign (b) on the bottom, resulting in log(ac) over log(b).
What is the process for expressing the expression '2 log a plus 5 log b minus 7 log c' as a single logarithm?
-The process involves moving the coefficients to the exponent position, resulting in log(a squared) plus log(b to the fifth) minus log(c to the seventh), and then combining them into a single logarithm with a and b on top and c on the bottom.
What is the significance of the coefficients in front of the logarithms?
-The coefficients in front of the logarithms determine whether the term will be on the top or bottom of the single logarithm expression and also dictate the exponent to which the base of the logarithm is raised.
How are negative coefficients treated when combining logarithms into a single logarithm?
-Negative coefficients are treated by placing the corresponding logarithmic term on the bottom of the fraction in the single logarithm expression.
What is the final expression for the third example in the transcript?
-The final expression for the third example is log(a to the one-third) plus log(c to the one-fourth) minus log(b to the two thirds) minus log(d to the four fifths), which can also be written in radical form.
Can the final expression of the third example be written in a different form?
-Yes, the final expression can also be written in radical form as the cube root of a times the fourth root of c divided by the cube root of b squared times the fifth root of d to the fourth.
What mathematical concept is demonstrated by converting the logarithmic expression into radical form?
-The conversion demonstrates the relationship between logarithms and radicals, showing that logarithmic expressions can be represented using radical notation.
Why is it helpful to express logarithmic expressions in both logarithmic and radical forms?
-Expressing logarithmic expressions in both forms is helpful because it allows for greater flexibility in problem-solving and can make certain calculations or manipulations easier depending on the context.
Outlines
📚 Condensing Multiple Logs into a Single Logarithm
This paragraph introduces the concept of combining multiple logarithmic expressions into a single logarithm, which is the inverse operation of expanding a single log into multiple logs. It begins with a basic example, showing how to condense 'log(a) + log(c) - log(b)' into 'log(ac/b)'. The explanation includes placing terms with positive signs in the numerator and negative signs in the denominator. The paragraph also provides a step-by-step guide for another example, '2 log(a) + 5 log(b) - 7 log(c)', which is simplified to 'log(a^2 * b^5 / c^7)'. The process involves moving coefficients to the exponent position and then combining them into a single logarithmic expression.
Mindmap
Keywords
💡Logarithm
💡Condense
💡Coefficient
💡Positive sign
💡Negative sign
💡Exponent
💡Radical form
💡Cube root
💡Fraction
💡Root
Highlights
Lesson focuses on condensing multiple logs into a single log, opposite of previous lesson.
Example provided: condensing log expressions with positive and negative coefficients.
Explanation on how to write a single log with positive terms on top and negative on bottom.
Second example given with coefficients 2, 5, -7, and how to express as a single log.
Demonstration of moving coefficients to the exponent position in log expressions.
Clarification on how to handle positive and negative signs when combining logs.
Introduction of a third example with fractional coefficients.
Step-by-step process shown for converting fractional log expressions into exponents.
Instruction on writing a single log with positive and negative terms correctly positioned.
Alternative representation of the final answer using radical form.
Emphasis on the importance of sign placement in log expressions.
Explanation of how to combine logs with different bases into a single expression.
Highlighting the mathematical properties used in simplifying log expressions.
Practical application of logarithmic properties to simplify complex expressions.
Final expression presented in both logarithmic and radical form for clarity.
Encouragement for students to practice converting between log and radical forms.
Summary of the lesson's goal to master the condensation of multiple logs into a single log.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: