Isoclines: A Way to Analyze Slope Fields

Brenda Edmonds
24 Aug 202008:13
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concept of slope fields and isoclines in the context of first-order differential equations. The instructor explains that 'iso' means same and 'klein' refers to slope, focusing on identifying locations in the slope field with constant slope. By examining a straightforward differential equation, the video emphasizes understanding the big picture without immediate reliance on computational tools. It illustrates how to sketch slope fields by determining areas of positive, negative, and zero slopes, using circles of varying radii as visual guides. The script concludes with a brief demonstration of using a computer software, D Field, to graph the phase plane and visualize the slope field, reinforcing the idea that isoclines are curves of constant slope.

Takeaways
  • 📈 The concept of slope fields was discussed, emphasizing the importance of isoclines.
  • 🌐 'Iso' means same and 'klein' means slope, referring to constant slopes in the field.
  • 🔢 A first-order differential equation was provided as an example to illustrate the concept.
  • 🖌️ The process of analyzing the slope field without a computer was outlined, focusing on a big-picture understanding.
  • 📊 The video included a comparison between hand-drawn and computer-graphic representations of the slope field.
  • ⭕️ A circle of radius √2 centered at the origin represents points of slope 0 in the slope field.
  • 🔼 The circle of radius √3 centered at the origin represents points of positive slope 1.
  • 🔽 A circle of radius 1 centered at the origin represents points of negative slope -1.
  • 🔄 The video demonstrated how to adjust settings in a software called d field to visualize the slope field.
  • 📝 The importance of identifying positive, negative, and zero slopes to understand the overall structure of the slope field was highlighted.
  • 🎯 The term 'isocline' was explained as the curve along which the slope is a particular constant value.
Q & A

  • What is the main focus of the video?

    -The main focus of the video is to discuss slope fields and isoclines in the context of first-order differential equations, emphasizing understanding the big picture without necessarily using a computer for graphing.

  • What does the term 'iso' mean?

    -The term 'iso' means 'same', which in the context of the video refers to the constant value of the slope in isoclines.

  • What does the term 'klein' mean in the context of the video?

    -In the context of the video, 'klein' is a mispronunciation of 'cline', which refers to lines of constant slope in a slope field.

  • How does the speaker suggest to visualize the slope field?

    -The speaker suggests visualizing the slope field by identifying the locations where the slope is zero, positive, and negative, and then sketching circles with different radii and slopes to get a big picture visualization of the slope field.

  • What is the significance of the circle with a radius of √2 centered at the origin?

    -The circle with a radius of √2 centered at the origin represents the points in the slope field where the slope is zero, indicating horizontal tangent lines to the curve.

  • How does the speaker describe the slope one isocline?

    -The speaker describes the slope one isocline as a circle with a radius of √3 centered at the origin, where the tangent lines have a slope of one, forming 45-degree angles with the coordinate axes.

  • What is the significance of the circle with a radius of 1 centered at the origin?

    -The circle with a radius of 1 centered at the origin represents the points in the slope field where the slope is negative one, with tangent lines forming negative 45-degree angles with the coordinate axes.

  • What is the main purpose of isoclines?

    -The main purpose of isoclines is to identify the curves along which the slope of the differential equation is constant, helping to understand the behavior of the solutions without having to plot the entire slope field.

  • How does the speaker change the default settings in D Field to match the example?

    -The speaker changes the default settings by replacing 'x as a function of t' with 'y as a function of x', and adjusts the independent variable to x. They also modify the equation to fit the form of the example and adjust the window settings to better visualize the slope field.

  • What numerical approximations can be seen in the slope field graphed on the computer?

    -In the slope field graphed on the computer, numerical approximations for the solution curves can be seen by clicking anywhere in the graph, which helps to visualize the solutions of the differential equation.

Outlines
00:00
📈 Introduction to Slope Fields and Isoclines

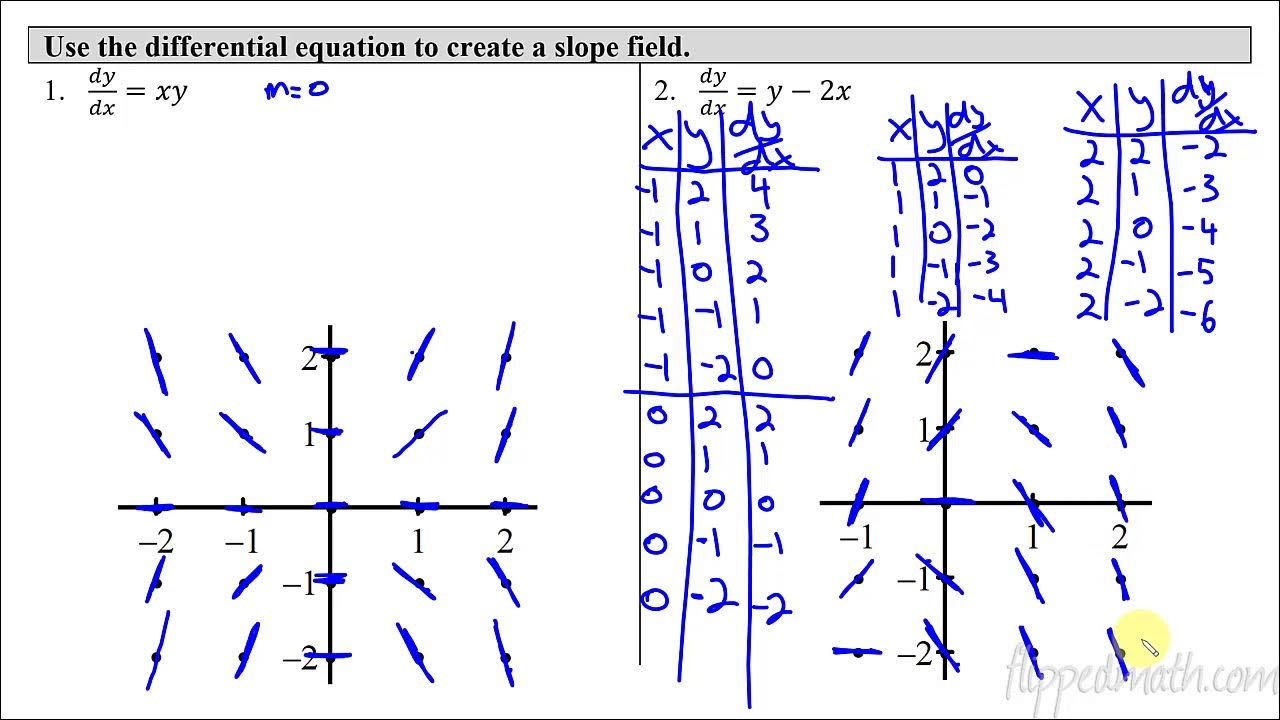
This paragraph introduces the concept of slope fields and isoclines, emphasizing the importance of understanding constant slopes within these fields. The speaker begins by defining the term 'isocline' and its relation to the slope of a function. They then present a first-order differential equation and discuss the approach to identifying points in the graph where the slope (dy/dx) is constant. The speaker also explains how to visualize these points by setting the right-hand side of the equation to a constant value, resulting in circles with specific radii and centers. The paragraph concludes with a brief mention of how to sketch these circles and understand the areas of positive, negative, and zero slopes.

05:02
🖥️ Using D-Field to Visualize Slope Fields and Isoclines

In this paragraph, the speaker continues the discussion on slope fields and isoclines by introducing the use of D-Field, a computational tool for visualizing these concepts. They explain the process of adjusting the settings in D-Field to match the differential equation being discussed, which involves changing the independent variable and the form of the equation. The speaker then demonstrates how to graph the phase plane and interpret the visual representation of the slope field, including the identification of isoclines as curves of constant slope. The paragraph emphasizes the importance of understanding positive, negative, and zero slopes and how to use these insights to analyze the slope field effectively.

Mindmap
Keywords
💡slope field
A slope field is a graphical representation of the slopes of a differential equation at every point in the Cartesian coordinate plane. In the video, the concept is used to visualize the behavior of a first-order differential equation, where the slope at any point (x, y) is given by the function dy/dx. The slope field helps in understanding the general behavior of solutions to the differential equation without having to solve it explicitly.
💡isoclines
Isoclines are the curves in a slope field where the slope of the differential equation is constant. They are important for understanding the structure of the solution set of a differential equation. In the context of the video, isoclines are used to identify regions where the solutions have the same slope, which can provide insights into the dynamics of the system described by the differential equation.
💡first-order differential equation
A first-order differential equation is an equation that involves an unknown function and its first derivative. These equations are fundamental in the study of calculus and are used to model a wide variety of phenomena in science, engineering, and economics. In the video, the author is working with a first-order differential equation to illustrate how to create and interpret a slope field.
💡dy/dx
The notation dy/dx represents the derivative of the function y with respect to x, which in the context of differential equations, signifies the slope of the tangent line to the curve at any point (x, y). It is a fundamental concept used to describe the rate of change of a function at a given point and is central to the analysis of differential equations.
💡circle of radius square root of 2
In the context of the video, this refers to a specific isocline in the slope field, which is a circle centered at the origin with a radius of √2. This circle represents all the points in the Cartesian plane where the slope of the differential equation is zero. The equation x^2 + y^2 = 2 defines this circle, and it is used to illustrate the concept of isoclines and how they appear in the slope field.
💡positive slope
A positive slope in the context of a slope field indicates that the function is increasing as the independent variable (often x) increases. In the video, the author discusses positive slopes in relation to isoclines and uses the example of a circle with a radius of √3 to illustrate points in the plane where the slope is consistently positive.
💡negative slope
A negative slope in a slope field means that the function is decreasing as the independent variable increases. This is the opposite of a positive slope and is characterized by tangent lines that make an angle with the coordinate axes that is obtuse (greater than 90 degrees but less than 180 degrees). The video uses the concept to illustrate regions in the slope field where the function is decreasing.
💡DField
DField is a software tool used to visualize and analyze differential equations. It allows users to plot slope fields and solution curves for various differential equations, providing a visual representation of the system's dynamics. In the video, the author uses DField to compare the hand-drawn slope field with the one generated by the software, to validate the visual understanding of the differential equation.
💡tangent lines
Tangent lines are straight lines that touch a curve at a single point without crossing it. In the context of a slope field, the slope of the tangent line at any point gives the instantaneous rate of change of the function at that point. The video discusses the use of tangent lines to visualize the slope of the differential equation at different points in the Cartesian plane.
💡phase plane
The phase plane is a graphical representation of the state space of a dynamical system, where each point in the plane represents a possible state of the system. In the context of differential equations, the phase plane plot helps visualize the trajectories of solutions and understand the long-term behavior of the system. The video uses the phase plane to display the slope field and the isoclines.
Highlights

The introduction of slope fields and isoclines, emphasizing the concept of iso meaning 'same' and klein meaning 'slope'.

The explanation of the first order differential equation and its relation to the slope field.

The method of visualizing the slope field without a computer by considering constant slopes and their corresponding values (positive, negative, and zero).

The identification of the circle of radius square root of 2 centered at the origin as the location of zero slope in the slope field.

The description of positive slope as areas where the rise and run are equal, forming 45-degree angles with the coordinate axes.

The illustration of the circle of radius square root of 3 to represent areas of positive slope one in the slope field.

The explanation of negative slope as areas with 45-degree angles to the coordinate axes but in the opposite direction, representing a slope of negative one.

The use of the term 'isocline' to describe curves along which the slope is constant, and the clarification of its meaning.

The demonstration of how to use the d field software to visualize the overall slope field and its parameters.

The caution about changing the default settings in d field to match the specific differential equation being used.

The process of adjusting the window settings in d field to better visualize the phase plane.

The observation of numerical approximations for solution curves within the d field visualization.

The strategy of starting with positive, negative, and zero slopes when looking for isoclines if no specific constants are given.

The emphasis on understanding the big picture of slope fields and the distribution of different slope values.

The practical approach to sketching isoclines and the importance of understanding their role in the slope field.

The discussion on how to interpret the differential equation and its implications for the slope field.

The application of the concept of isoclines to homework problems and their relevance to understanding slope fields.

Transcripts

Browse More Related Video

Calculus AB/BC – 7.3 Sketching Slope Fields

Slope Fields | Calculus

Lec 1 | MIT 18.03 Differential Equations, Spring 2006

Calculus 1: Slope Fields Examples

Calculus AB/BC – 7.4 Reasoning Using Slope Fields

Slope Fields

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Differential EquationsSlope FieldsIsoclinesMathematical AnalysisConstant SlopeVisual RepresentationEducational ContentMath TutorialPositive Negative Zero SlopesD-Field Software