Factorial with lambda calculus
TLDRThe video script discusses the implementation of a factorial function using pure Lambda calculus, a formal system in mathematical logic. It explains the concept of defining a Lambda function that takes a single argument and outlines the recursive process for calculating factorials. The script also touches on the use of the Y combinator to enable recursion in a language that doesn't natively support it. The author demonstrates the factorial function with examples, including calculating factorials of zero, one, two, three, and four, highlighting the complexity and the process involved in Lambda calculus computations.
Takeaways
- 📚 The video discusses implementing a factorial function in pure Lambda calculus, a fundamental concept in functional programming.
- 🔑 The factorial function is defined in terms of a Lambda function that takes a single argument and uses recursion to calculate the factorial.
- 🎯 The base case for the factorial function is when the input is zero, in which case the function returns one.
- 🔄 The function uses recursion by multiplying the input number with the factorial of the number minus one, showcasing the self-referential nature of Lambda calculus.
- 🔢 The script introduces the use of a 'zero?' function to check if the input is zero, which is a necessary part of the factorial definition.
- 📈 The 'Y combinator' is used to enable recursion in the factorial function, as Lambda calculus does not natively support recursion.
- 🔧 The video also mentions other Lambda calculus terms such as 'predecessor', 'if', and 'multiplication', which are essential for the factorial function to work.
- 🛠️ The presenter demonstrates the factorial function with various inputs, such as zero, one, two, and three, to show how the function computes the result.
- 🤖 The video includes a live demonstration using a Lambda calculus calculator, which may have some limitations in recognizing certain Lambda terms.
- 📉 The presenter notes that the calculator does not evaluate all expressions immediately, instead waiting for the user to proceed to the end of the document.
- 📝 The factorial function in Lambda calculus, while interesting, can be tedious to read and may benefit from improvements in the calculator's ability to simplify expressions.
Q & A
What is the main topic discussed in the video script?
-The main topic discussed in the video script is the implementation of a factorial function in Lambda calculus.
What is Lambda calculus?
-Lambda calculus is a formal system in mathematical logic and computer science for expressing computation by way of function abstraction and application using variable binding and substitution.
What is the factorial function in the context of Lambda calculus?
-In the context of Lambda calculus, the factorial function is a higher-order function that takes a number and returns the product of all positive integers less than or equal to that number, defined recursively.
How does the video script define the factorial function in terms of Lambda calculus?
-The script defines the factorial function by using a Lambda function that checks if the input number is zero and returns one if true, otherwise it multiplies the number by the factorial of the number minus one, using recursion.
What is the Y combinator in Lambda calculus?
-The Y combinator is a fixed-point combinator in Lambda calculus, which is used to implement recursion. It allows the creation of recursive functions without relying on named functions or loops.
Why is the Y combinator necessary for the factorial function in this script?
-The Y combinator is necessary because Lambda calculus does not have built-in support for recursion, and the Y combinator provides a way to achieve recursion by creating a fixed-point for the factorial function.
What is the role of the 'if' term in the definition of the factorial function in the script?
-The 'if' term is used to check if the input number is zero. If it is, the function returns one; otherwise, it proceeds with the recursive multiplication part of the factorial definition.
What are some of the Lambda terms provided in the script for supporting the factorial function?
-The script mentions Lambda terms for checking if a number is zero, for the predecessor function (minus one), the Y combinator, an 'if' term, and a multiplication term, all of which are necessary for the factorial function to work correctly.
How does the script handle the multiplication of the factorial function with the number minus one?
-The script uses a multiplication term that multiplies the input number with the factorial of the number minus one, achieved through a recursive call to the factorial function itself.
What is the final step in implementing the factorial function as described in the script?
-The final step is to apply the helper function for the factorial to the Y combinator, which returns the factorial function as a fixed point, allowing for the calculation of factorials for any given number.
What issues are mentioned regarding the calculator used in the script?
-The script mentions that the calculator does not recognize the Lambda expressions inside the definitions well and that it may be better if the author improved the recognition. Additionally, the script notes that the calculator does not evaluate all expressions immediately but waits until the end of the document before providing results.
Outlines
🧠 Implementing Factorial in Lambda Calculus
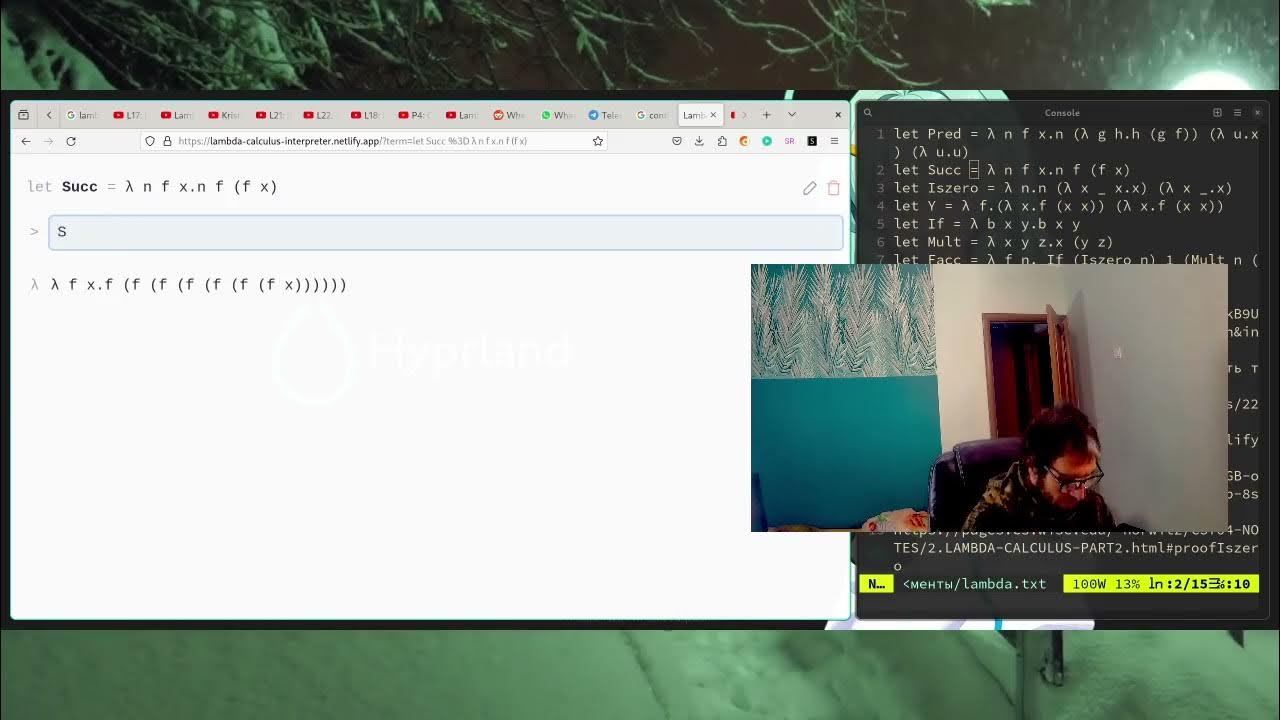
The script introduces the concept of implementing a factorial function using pure Lambda calculus. It explains that everything in Lambda calculus is defined in terms of functions, and the factorial function is no exception. The factorial function is defined as a Lambda function that takes a single argument. The script outlines the recursive nature of the factorial function, where if the input is zero, it returns one, and otherwise, it multiplies the input by the factorial of the input minus one. It also touches on the use of recursion in Lambda calculus, mentioning the need for self-reference and the use of argument abstraction to achieve this.
🔄 Utilizing the Y-Combinator for Recursion
This paragraph delves into the use of the Y-combinator to achieve recursion in Lambda calculus, which does not natively support it. The script describes how to define a function that applies another function to itself, effectively creating a fixed point. It mentions the need for auxiliary functions such as a predecessor, a boolean check for zero, and a multiplication function. The Y-combinator is then applied to a helper function to produce the factorial function. The script also notes the limitations of the Lambda calculus calculator used in the demonstration, which does not recognize certain constructs within definitions.
📊 Testing the Factorial Function in Lambda Calculus
The final paragraph discusses the practical testing of the implemented factorial function in Lambda calculus. It describes the process of running the function with different inputs, such as zero, one, and two, and observing the expected results. The script also attempts to calculate the factorial of larger numbers like four and notes the increased complexity and computation time. It highlights an issue with the calculator's output, where it incorrectly displays the factorial of four as 26 instead of the correct 24. The author suggests that improvements could be made to the calculator for better readability and functionality.
Mindmap
Keywords
💡Lambda Calculus
💡Factorial Function
💡Recursion
💡Y Combinator
💡Zero
💡Multiplication
💡Predecessor
💡Function Abstraction
💡Application
💡Fixed Point
💡Calculator
Highlights
Introduction to implementing the factorial function in pure Lambda calculus.
Defining the factorial function as a Lambda term that takes a single argument.
Using a Lambda function to handle the base case where n is zero, returning one.
Recursive definition of factorial for cases where n is not zero, involving multiplication with n-1.
Explanation of how to check if a number is zero using a Lambda term.
The use of a self-referential Lambda term to achieve recursion in Lambda calculus.
Misstep in the transcription process due to case sensitivity in Lambda terms.
Introduction of helper functions like predecessor, Y combinator, if, and multiplication terms.
Correcting the Lambda term to use uppercase letters for proper compilation.
Demonstration of how to apply the factorial function using the Y combinator.
Testing the factorial function with different inputs like zero, one, and two.
Observation of the calculator's behavior and its handling of Lambda calculus expressions.
The factorial function's successful execution for the input of three.
The complexity and length of the computation process for larger inputs like four.
Incorrect result for the factorial of four, indicating a potential error in the process.
The tedious nature of reading and interpreting the output of the Lambda calculus calculator.
Suggestion to improve the calculator's ability to handle and display Lambda calculus expressions.
Final thoughts on the interesting and unique implementation of a Lambda calculus calculator in JavaScript.
Transcripts
Browse More Related Video

Essentials: Functional Programming's Y Combinator - Computerphile

Y combinator and recursion in haskell (implement fib without recursion)

The most intriguing discovery of Computer Science: the Y combinator demystified.
Lambda Calculus Calculator

Lambda Calculus: The foundation of functional programming, and the simplest programming language
Programming Languages - The Lambda Lecture
5.0 / 5 (0 votes)
Thanks for rating: