Lambda Calculus - Fundamentals of Lambda Calculus & Functional Programming in JavaScript

Fullstack Academy

25 Aug 201762:15

EducationalLearning

32 Likes 10 Comments

TLDRIn this talk, Gabriel explores the lambda calculus, a formal system for function definition and application, demonstrating how it forms the basis of functional programming languages. He discusses combinators, Church encodings for booleans, and the elegance of mathematical beauty in lambda calculus, highlighting its practical applications in modern programming.

Takeaways

😀 Gabriel, the speaker, is an instructor at Full-Stack Academy of Code and has a strong presence on social media under the name G Lebec.
📚 The talk introduces the concept of lambda calculus, a formal system for function definition, application, and notation, which is foundational to functional programming.
🔧 Lambda calculus uses basic constructs like function application, variables, and abstraction, and it manipulates these without the need for traditional mathematical operations like + or =.
🎯 The identity combinator is highlighted as a fundamental function that returns its input unchanged, demonstrating the concept of functions as first-class citizens in lambda calculus.
📝 The script explains the use of lambda notation for defining anonymous functions, a key feature of lambda calculus and functional programming paradigms.
🔄 Beta reduction is discussed as the process of evaluating function applications in lambda calculus, which simplifies expressions by substituting parameters with their arguments.
💡 The concept of combinators, such as the Mockingbird and Kestrel, is introduced as functions that can generate other functions, showcasing the expressive power of lambda calculus.
🚫 The halting problem is mentioned, illustrating the challenge of determining whether a lambda expression will always evaluate to a result or go on indefinitely.
🔢 Church encoding is presented as a method to represent data types like booleans and numbers within lambda calculus, which lacks native support for these types.
🔄 The talk explores the implementation of logical operations like NOT, AND, and OR using only lambda calculus constructs, demonstrating the system's computational completeness.
🔍 The historical context of lambda calculus and its connection to the work of mathematicians like Alonzo Church, Haskell Curry, and Alan Turing is briefly touched upon, emphasizing the significance of lambda calculus in the field of theoretical computer science.

Q & A

What is the identity function in the context of the lambda calculus?
-The identity function is a function that takes an input and returns the same input. In the lambda calculus, it is represented as a function that takes a single parameter and returns that parameter. It is a fundamental concept where the identity of any value X is X itself.
What is lambda calculus and why is it significant?
-Lambda calculus is a formal system in mathematical logic for expressing computation by function abstraction and application. It is significant because it provides a theoretical foundation for programming languages and is the basis for functional programming languages. It demonstrates how functions can be treated as first-class citizens.
What does the term 'beta reduction' refer to in lambda calculus?
-Beta reduction is a process in lambda calculus that involves substituting the parameters of a function with its arguments. It is the act of evaluating function invocations by replacing the function's parameters with the provided arguments in the function's body.
How does the 'Mockingbird' combinator function in lambda calculus?
-The 'Mockingbird' combinator is a function that takes another function as input and applies it to itself. It is an example of a higher-order function, demonstrating the ability to use functions as arguments and return values in lambda calculus.
What is the 'Kestrel' combinator and how does it behave?
-The 'Kestrel' combinator, also known as the 'const' function in Haskell, takes two arguments but always returns the first one. It is a function that disregards its second argument and is used to create constant functions.
What is the significance of combinators in lambda calculus?
-Combinators in lambda calculus are functions that can be combined to create more complex functions. They are significant because they can be used to build all computable functions, demonstrating the expressive power of lambda calculus.
How does the 'Kite' combinator function in lambda calculus?
-The 'Kite' combinator is a function that takes two arguments and returns the second one. It is similar to the 'Kestrel' but inverts the order of the arguments it returns.
What is the 'Cardinal' combinator and what does it do?
-The 'Cardinal' combinator is a function that takes a function and two arguments, and applies the function to the arguments in reverse order. It effectively flips the order of the arguments for the function application.
Why are there bird names for some combinators in lambda calculus?
-The bird names for some combinators come from Raymond Smullyan's book 'To Mock a Mockingbird'. Smullyan used bird names as a metaphor to explain combinatory logic in a more accessible and engaging way.
What is the relationship between lambda calculus and Turing machines?
-Lambda calculus and Turing machines are equivalent in terms of computational power. They both can calculate anything that is computable, demonstrating the fundamental principles of computation theory.
What are Church encodings and why are they important in lambda calculus?
-Church encodings are a way of representing data types such as booleans and numbers using only functions in lambda calculus. They are important because they allow for the representation of complex data structures and operations without the need for primitive data types or control structures.

Outlines

00:00

👋 Introduction to Lambda Calculus

Gabriel, an instructor at Full-Stack Academy of Code, introduces the topic of the talk, which is the lambda calculus. He explains that the talk will focus on functions and their applications, avoiding traditional JavaScript syntax. Gabriel introduces the identity function, which simply returns its input, and discusses how functions can be used as arguments and nouns in lambda calculus. He also mentions resources available on his GitHub for further learning.

05:00

🧠 Understanding Lambda Abstraction

The talk delves into the concept of lambda abstraction, which is a way of defining functions in lambda calculus. Gabriel explains that lambda calculus is a small framework for manipulating symbols, and it involves variables, expressions, function definitions, and groupings. He emphasizes the immutability of variables and the concept of function application through juxtaposition without parentheses. The explanation includes examples of curried functions and how they are applied in a step-by-step manner.

10:01

🔍 Exploring Beta Reduction

Beta reduction is introduced as the process of evaluating function invocations in lambda calculus. Gabriel demonstrates how to apply a function to its argument by substituting the argument into the function's body. He explains that this process can continue until no more reducible expressions are left, resulting in a beta normal form. The talk also touches on the halting problem, which questions whether a given expression will ever stop evaluating.

15:04

🐦 Combinators: Mockingbird and Kestrel

Gabriel discusses combinators, which are functions that can be combined to create new functions. He introduces the Mockingbird combinator, which applies a function to itself, and the Kestrel combinator, which returns the first of its two arguments. The talk explores the properties of these combinators and their applications, including the concept of currying and the creation of constant functions.

20:07

📚 Historical Context of Lambda Calculus

The talk provides a historical overview of lambda calculus and its development. Gabriel mentions early pioneers like Giuseppe Peano, Gottlob Frege, Bertrand Russell, and Alonzo Church. He also discusses the contributions of Haskell Curry and the impact of Raymond Smullyan's book 'To Mock a Mockingbird,' which uses bird metaphors to explain combinatory logic.

25:09

🔢 Church Encodings and Boolean Logic

Gabriel explains how boolean logic can be represented in lambda calculus using Church encodings. He demonstrates how to encode true and false as functions and how to implement logical operations like negation, conjunction, and disjunction using combinators. The talk also covers the concept of extensional and intentional equality in the context of lambda calculus.

30:09

🤔 The Power of Combinators

The talk explores the concept of combinators further, discussing how primitive combinators can be combined to generate more complex ones. Gabriel introduces the Cardinal combinator, which flips the order of function arguments, and demonstrates its use in creating new functions. The discussion highlights the elegance and utility of combinatory logic in functional programming.

35:09

🎓 Conclusion and Further Exploration

Gabriel concludes the talk by emphasizing the fun and beauty of lambda calculus. He mentions the practical benefits of understanding combinatory logic for functional programming languages like Haskell and Lisp. The talk also touches on the Y Combinator, which enables recursion in lambda calculus, and the Z Combinator, which is a variation that can be demonstrated in non-lazy languages like JavaScript.

Mindmap

Keywords

💡Lambda Calculus

Lambda Calculus is a formal system in mathematical logic for expressing computation by function abstraction and application. It is the foundation of functional programming languages. In the video, Lambda Calculus is used to demonstrate how functions can be manipulated and combined to perform complex tasks, such as boolean logic and arithmetic, without the need for traditional control structures like loops or conditionals.

💡Identity Function

The Identity Function is a simple function that returns its input unchanged. In the context of the video, it is used to illustrate the basic concept of function application in Lambda Calculus. The identity function is represented as 'identity' in JavaScript and 'id' in Haskell, and it is a fundamental building block in the lambda calculus.

💡Combinator

A Combinator in Lambda Calculus is a higher-order function that uses function application and abstraction to perform operations without using any free variables. Examples given in the video include the identity combinator, the self-application combinator (Mockingbird), and the constant combinator (Kestrel). These combinators are used to build more complex functions and illustrate the power of functional composition.

💡Beta Reduction

Beta Reduction is a process in Lambda Calculus that involves substituting the parameters of a function with its arguments to evaluate the function's body. It is a fundamental operation in the calculus, allowing for the simplification of expressions. In the video, beta reduction is used to demonstrate how functions are applied and how they can be reduced to their simplest form.

💡Currying

Currying is the process of transforming a function that takes multiple arguments into a sequence of functions, each with a single argument. This concept is central to functional programming and is demonstrated in the video through the creation of functions that take one argument and return another function. The video uses currying to show how functions can be nested and applied in a step-by-step manner.

💡Church Encoding

Church Encoding is a method of representing data types and operations in Lambda Calculus using only functions. It is named after Alonzo Church, the founder of Lambda Calculus. In the video, Church Encoding is used to represent boolean values and arithmetic operations as functions, showing how complex data types can be manipulated using only function application.

💡Y Combinator

The Y Combinator is a famous combinator in Lambda Calculus that enables recursion by creating a fixed-point combinator. It is used to demonstrate how recursion can be achieved in a language that does not inherently support it. The video mentions the Y Combinator as a brain teaser, highlighting its role in enabling recursive functions in a language without loops or recursion.

💡Kestrel

The Kestrel is a combinator in Lambda Calculus that takes two arguments and returns the first one. It is used in the video to illustrate the concept of constant functions and to demonstrate how simple combinators can be combined to create more complex behaviors. The Kestrel is also used in the creation of other combinators, such as the Kite.

💡Mockingbird

The Mockingbird is a combinator that takes a function as an argument and applies it to itself. It is used in the video to demonstrate self-application and to illustrate the concept of recursion in Lambda Calculus. The Mockingbird is also used to create an infinite loop, highlighting the potential for divergence in lambda expressions.

💡Z Combinator

The Z Combinator, also known as the Thue combinator, is a variation of the Y Combinator that introduces laziness into the recursion. It is used in the video to demonstrate how recursion can be implemented in a lazy language like Haskell, where evaluation is deferred until necessary. The Z Combinator is mentioned as a solution to the problem of infinite recursion in strict languages like JavaScript.

Highlights

Introduction to Gabriel, the instructor at Full-Stack Academy of Code, and his social media presence.

Explaining the identity function in JavaScript and its implementation in Haskell.

Introduction to lambda notation and lambda calculus, emphasizing its role in defining functions.

Discussion on variables in lambda calculus being immutable and the concept of binding.

Explanation of function application in lambda calculus through juxtaposition without parentheses.

Introduction to the concept of currying in lambda calculus.

Demonstration of a curried addition function in lambda calculus.

Explanation of function definition in lambda calculus using lambda abstraction.

Introduction to beta reduction in lambda calculus as the process of evaluating function invocations.

Discussion on the halting problem and its relation to lambda calculus expressions.

Introduction to the Mockingbird combinator and its behavior in lambda calculus.

Explanation of the Kestrel combinator and its role in returning the first argument.

Demonstration of deriving the Kite combinator from the Identity and Kestrel combinators.

Introduction to the Cardinal combinator and its function to flip arguments.

Discussion on the historical context of lambda calculus and its relation to Turing machines.

Explanation of how lambda calculus can represent boolean logic without traditional boolean operators.

Introduction to Church encodings and their use in representing boolean values in lambda calculus.

Demonstration of implementing the NOT function in lambda calculus using combinators.

Introduction to the concept of extensional and intentional equality in lambda calculus.

Explanation of how lambda calculus can be used to represent arithmetic operations.

Discussion on the practical applications of lambda calculus in functional programming languages.

Introduction to the Y Combinator and its role in enabling recursion in lambda calculus.

Transcripts

Browse More Related Video

What is Lambda Calculus? (ft. Church Encodings)

Lambda Calculus: The foundation of functional programming, and the simplest programming language

Lambda Calculus - Computerphile

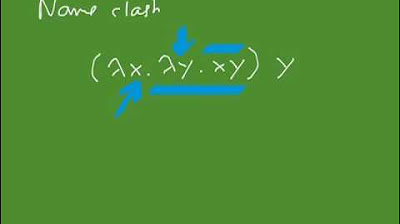
The Lambda Calculus, part 1 1 Syntax and semantics

lambda calculus review

A Flock of Functions: Lambda Calculus and Combinatory Logic in JavaScript | Gabriel Lebec @ DevTalks

Related Tags

Lambda Calculus Functional Programming Combinatory Logic JavaScript Higher-Order Functions Currying Church Encoding Recursive Functions Y Combinator Programming Language