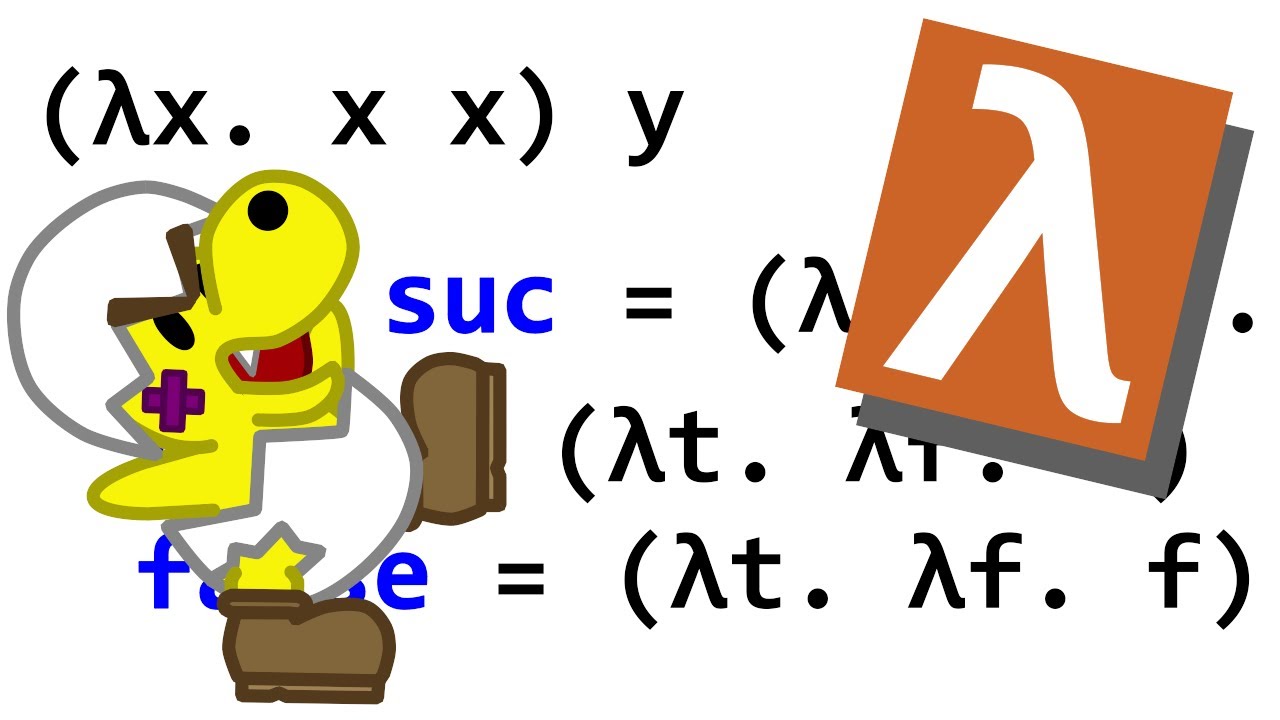Lambda Calculus - Computerphile
TLDRThis video explores Lambda Calculus, a foundational concept in computer science invented by Alonzo Church. It delves into the origins, utility, and applications of Lambda Calculus, including its equivalence with Turing machines, its role in functional programming languages like Haskell, and its presence in modern programming languages. The video also demonstrates encoding logical values and recursion using Lambda Calculus, and intriguingly draws parallels with biological self-replication.
Takeaways
- 📚 The Lambda Calculus is a foundational concept in Computer Science, introduced by Alonzo Church, a mathematician at Princeton University.
- 🧑🏫 Alonzo Church was also the PhD supervisor of Alan Turing, famous for his invention of the Turing machines, which are state-based models of computation.
- 🔄 The Church-Turing hypothesis suggests that the functional approach of Lambda Calculus and the state-based approach of Turing machines are equivalent in their computational power.
- 📦 In Lambda Calculus, functions are considered as black boxes that take inputs and produce outputs without revealing their internal workings.
- 🔢 Lambda Calculus uses a simple syntax involving lambda expressions to define functions, such as incrementing a number or calculating the sum of two numbers.
- 🔄 The process of applying a function in Lambda Calculus involves substitution, where the input values replace the variables within the function's definition.
- 🤖 Lambda Calculus can encode any computation, aligning with the Church-Turing hypothesis, and is the basis for functional programming languages like Haskell.
- 🌐 Modern programming languages, including Java, C#, and F#, have incorporated elements of Lambda Calculus, making it relevant for today's computer scientists.
- 🔧 Lambda Calculus lacks built-in data types and control structures, requiring the encoding of concepts like logical values, TRUE and FALSE, to perform operations.
- 🔄 TRUE and FALSE in Lambda Calculus are encoded using lambda expressions that choose between two options, providing a foundation for logical operations.
- ⚙️ The Y combinator is a famous expression in Lambda Calculus that enables recursion, a key mechanism for defining functions in terms of themselves.
Q & A
What is the Lambda Calculus?
-The Lambda Calculus is a formal system in mathematical logic and computer science for expressing computation based on function abstraction and application. It was invented by Alonzo Church and is used to define functions as black box processes that take inputs and produce outputs without any internal state.
Who invented the Lambda Calculus?
-Alonzo Church, a mathematician at Princeton University, invented the Lambda Calculus.
What is the relationship between Alonzo Church and Alan Turing?
-Alonzo Church was the PhD supervisor of Alan Turing, who is famous for inventing Turing machines. Both Church and Turing independently developed foundational concepts in computer science, with Church focusing on the Lambda Calculus and Turing on Turing machines.
What is the Church-Turing hypothesis?
-The Church-Turing hypothesis states that any function that can be computed by an algorithm can be computed by a Turing machine, and vice versa. It suggests that the Lambda Calculus and Turing machines are equivalent in their computational power.
How are functions defined in the Lambda Calculus?
-In the Lambda Calculus, functions are defined using lambda expressions. For example, a function that increments a number x can be written as 'lambda x, x + 1', and a function that adds two numbers x and y can be written as 'lambda x, lambda y, x + y'.
What are the basic components of the Lambda Calculus?
-The Lambda Calculus consists of variables (like x, y, z), a way of building functions using lambda notation, and a way of applying functions. It does not have built-in data types, control structures, or other complexities found in modern programming languages.
Why is the Lambda Calculus important in computer science?
-The Lambda Calculus is important because it can encode any computation, making it a fundamental concept in computer science. It serves as the basis for functional programming languages like Haskell and is now incorporated into many major programming languages, reflecting its relevance in modern computing.
How can logical values be encoded in the Lambda Calculus?
-Logical values like TRUE and FALSE can be encoded in the Lambda Calculus using lambda expressions. For instance, TRUE can be represented as 'lambda x, lambda y, x', which chooses the first of two inputs, and FALSE as 'lambda x, lambda y, y', which chooses the second.
What is the NOT function in the Lambda Calculus?
-The NOT function in the Lambda Calculus can be defined as 'lambda b, b FALSE TRUE'. This function takes a logical value b and applies it to FALSE and TRUE, effectively negating the value.
What is the Y combinator in the Lambda Calculus?
-The Y combinator is a famous lambda expression that enables recursion in the Lambda Calculus. It is a key component for defining functions that call themselves, which is not inherently supported in the Lambda Calculus due to its simplicity.
What is the connection between the Lambda Calculus and biology as mentioned in the script?
-The script suggests a philosophical connection between the Lambda Calculus and biology, particularly in the way the Y combinator's structure resembles the double helix structure of DNA. This resemblance hints at a deeper connection between self-replication in biology and recursion in programming.
Outlines
📚 Introduction to Lambda Calculus
The video script introduces Lambda Calculus, a foundational concept in computer science, focusing on its origin, utility, and history. Alonzo Church, a mathematician at Princeton University, is credited with its invention, aiming to define functions from a computational perspective. The script highlights the connection between Church and Alan Turing, Church's PhD student who invented Turing machines. It explains the equivalence of these two models of computation under the Church-Turing hypothesis. The concept of functions as black boxes with inputs and outputs is discussed, emphasizing their purity and lack of internal state, contrasting with Turing's state-based computation model. Basic syntax for defining functions in Lambda Calculus is introduced, using lambda expressions for increment and addition functions as examples.
🔗 Lambda Calculus and Computational Equivalence
This paragraph delves into the significance of Lambda Calculus, asserting its ability to encode any computation, aligning with the Church-Turing hypothesis. It discusses the formal equivalence between Turing machines and Lambda Calculus programs, indicating that one can be translated into the other. The script also positions Lambda Calculus as the basis for modern functional programming languages like Haskell, which compiles down to a core language fundamentally based on Lambda Calculus. It mentions the increasing presence of Lambda Calculus in major programming languages, making it essential knowledge for computer scientists. The paragraph concludes with examples of encoding logical values TRUE and FALSE within Lambda Calculus, demonstrating the system's capability to handle logical operations without built-in data types.
🧠 Lambda Calculus and Recursion
The final paragraph of the script explores the concept of recursion in Lambda Calculus, a system traditionally lacking built-in control structures or data types. It introduces the Y combinator, a famous Lambda Calculus expression invented by Haskell Curry, which enables recursion—a mechanism for defining functions in terms of themselves. The script suggests a philosophical connection between the Y combinator's structure and the double helix of DNA, drawing a parallel between self-replication in biology and recursion in programming. It concludes with an anecdote about someone who chose to tattoo the Y combinator, reflecting its significance in the field of computer science.
Mindmap
Keywords
💡Lambda Calculus
💡Alonzo Church
💡Alan Turing
💡Church-Turing hypothesis
💡Functional programming
💡Haskell
💡Lambda expression
💡Substitution
💡Y combinator
💡Encoding
💡Recursion
Highlights
Lambda Calculus is a fundamental concept in Computer Science, focusing on the computational perspective of functions.
Alonzo Church, a mathematician at Princeton University, invented Lambda Calculus to explore the notion of a function in computation.
Church was the PhD supervisor of Alan Turing, who invented Turing machines, a state-based model of computation.
Lambda Calculus and Turing machines, though different, are equivalent in terms of computational power, forming the basis of the Church-Turing hypothesis.
In Lambda Calculus, functions are viewed as black boxes that process inputs to produce outputs without internal state.
Functions in Lambda Calculus are defined using a simple syntax with lambda notation, such as lambda x.x + 1 for an increment function.
Lambda Calculus can encode any computation, aligning with the Church-Turing hypothesis that it can represent any sequential programming language.
Lambda Calculus serves as the foundation for functional programming languages like Haskell and ML, influencing their core language structure.
Major programming languages today, including Java and C#, incorporate elements of Lambda Calculus.
Lambda Calculus lacks built-in data types and control structures, necessitating encoding for operations like logical values and recursion.
Logical values TRUE and FALSE can be encoded in Lambda Calculus using lambda expressions that choose between two inputs.
The NOT logical operator can be defined in Lambda Calculus by applying a logical value to FALSE and TRUE, demonstrating its negation.
Lambda Calculus expressions can be expanded and substituted to demonstrate the behavior of logical operations, such as NOT.
The Y combinator, a famous Lambda Calculus expression, enables recursion, a key mechanism for defining functions in terms of themselves.
Haskell Curry, who invented the Y combinator, influenced the naming of the Haskell programming language.
There is a philosophical connection drawn between the structure of the Y combinator and the self-replication mechanism in biology, specifically DNA.
The Y combinator is significant enough in the field of computer science that some individuals have chosen to tattoo it permanently.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: