Calculus Work Pump Water From a Circular Swimming Pool
TLDRThis video explains how to calculate the work required to pump water out of a circular swimming pool. The pool has a diameter of 24 feet, sides 5 feet high, and water depth of 4 feet. Using the weight of water (62.5 pounds per cubic foot), the presenter demonstrates the calculation step-by-step, including drawing a slice of the pool, finding its volume, and integrating the force over the distance to get the total work. The final answer is 108,000π foot-pounds. The video also references another example involving an inverted cone.
Takeaways
- 🏊♂️ The video discusses calculating the work required to pump water out over the sides of a circular swimming pool.
- 📏 It provides the dimensions of the pool: a diameter of 24 feet, a height of 5 feet, and a water depth of 4 feet.
- 💧 The weight of water is given as 62.5 pounds per cubic foot, which is used to calculate the force exerted by the water.
- 📈 The process involves breaking down the problem into slices of water and calculating the work done on each slice.
- 📐 The volume of each water slice is calculated using the formula for the volume of a cylinder: π * radius^2 * height (Δx).
- 🔢 The force on each slice is determined by multiplying the volume of the slice by the weight of water per cubic foot.
- 🔑 The work done on each slice is the product of force and the distance (X) the slice must be moved to clear the pool's edge.
- ∫ The total work is found by integrating the work done per slice over the range from the top to the bottom of the water.
- 📉 The integration limits are from 1 foot (top of the water) to 5 feet (top of the pool), representing the range of distances the water must be moved.
- 📚 The final calculation yields the total work in foot-pounds, which is 108,000π.
- 🔗 The video also references another video on a similar topic, involving pumping water out of an inverted cone, indicating a series of related educational content.
Q & A
What is the main topic of the video?
-The video discusses the process of calculating the work required to pump water out over the sides of a circular swimming pool.
What are the dimensions of the swimming pool mentioned in the video?
-The swimming pool has a diameter of 24 feet, a height of 5 feet, and the depth of the water is 4 feet.
What is the weight of water per cubic foot, according to the video?
-The weight of water per cubic foot is given as 62.5 pounds.
How does the video suggest to approach the problem of calculating work?
-The video suggests looking at a single slice of water at a time, calculating the work for that slice, and then integrating to find the total work.
What is the formula for the volume of a water slice in the pool?
-The volume of a water slice is given by the formula π * (radius squared) * height of the slice, which is π * (12 feet)^2 * Δx.
How is the force on a water slice calculated in the video?
-The force on a water slice is calculated by multiplying the volume of the slice by the weight of water per cubic foot, resulting in 62.5 * (144π * Δx).
What is the formula for work done on a water slice?
-The work done on a water slice is the force times the distance, which is 9000π * Δx * x, where x is the distance from the slice to the top of the pool.
What is the range of integration for calculating the total work?
-The range of integration is from x = 1 foot to x = 5 feet, representing the distance from the top of the water to the top and bottom of the pool, respectively.
What is the final result of the integration for the total work?
-The final result of the integration is 108,000π foot-pounds, which represents the total work required to pump all the water out.
Is the method demonstrated in the video specific to water or can it be applied to other substances?
-The method demonstrated is not specific to water and can be applied to any substance, as long as the weight per unit volume of that substance is known.
Does the video mention any other related content or resources?
-Yes, the video mentions another video on pumping water out of an inverted cone and suggests checking out the playlist 'Calculus Integrals' for more related content.
Outlines
🏊♂️ Calculating Work to Pump Water Over a Pool's Side
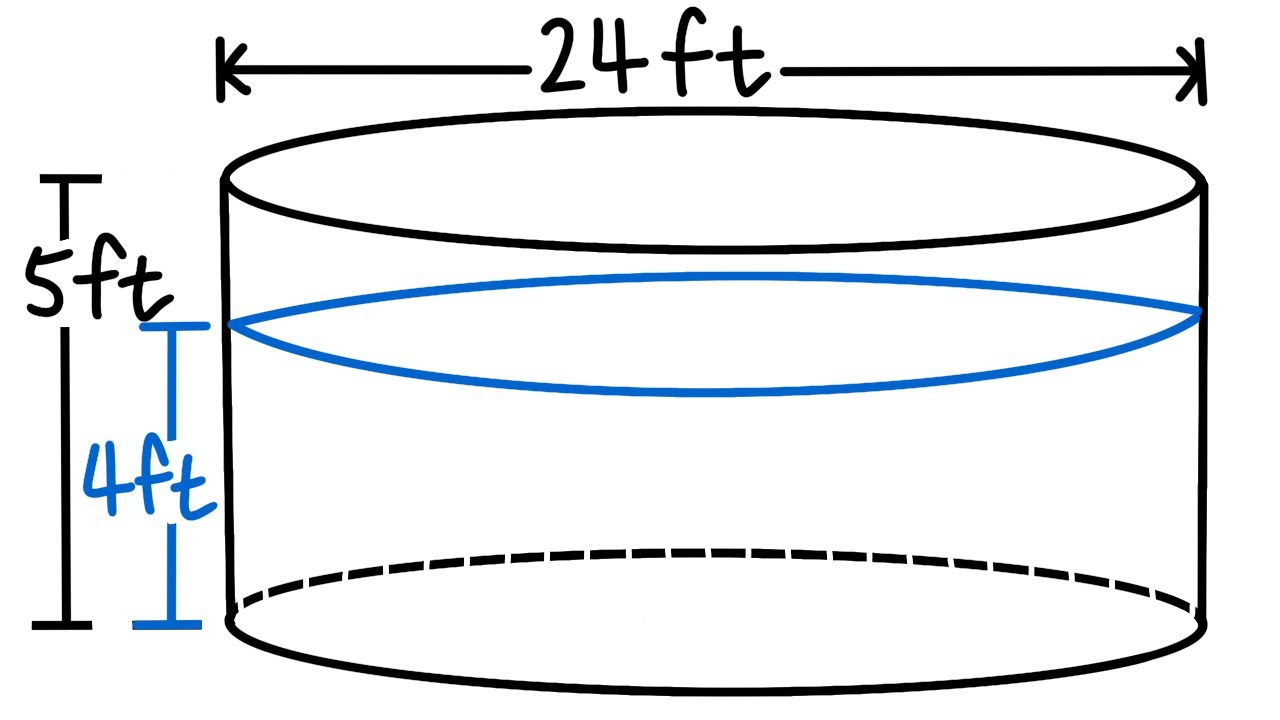
This paragraph introduces a problem-solving scenario involving a circular swimming pool with a diameter of 24 feet, sides 5 feet high, and water depth of 4 feet. The task is to calculate the work required to pump all the water over the pool's sides. The script emphasizes the importance of understanding the physical dimensions and the weight of water, which is given as 62.5 pounds per cubic foot. The approach involves visualizing the pool, considering a thin vertical slice of water, and calculating the work needed to move this slice. The concept of work as force times distance is introduced, and the force is determined by the volume of the water slice multiplied by the weight of water. The volume calculation for the slice is derived using the formula for the volume of a cylinder, πr^2h, where r is the radius and h is the height (or thickness) of the slice, Δx.
📚 Integrating to Find Total Work for Pumping Water
The second paragraph delves into the mathematical process of calculating the total work required to pump water out of the pool. It starts by establishing the formula for work as force times distance for a single slice of water and then explains the need to integrate this work over all slices to find the total work. The force for each slice is given as 9000π times Δx, derived from the weight of water per cubic foot and the volume of the slice. The integration process is outlined, with the constant 9000π pulled out of the integral, and the integration limits set from the top of the water (1 foot from the top of the pool) to the top of the pool (5 feet). The resulting integral calculation simplifies to 4500π times the square of the distance (x), evaluated from 1 to 5, yielding a total work of 108,000π foot-pounds. The paragraph concludes with a reference to another video on a similar topic and an invitation for viewers to check out the calculus integrals playlist for more related content.
Mindmap
Keywords
💡Work
💡Pumping
💡Swimming Pool
💡Diameter
💡Height
💡Depth
💡Volume
💡Force
💡Integration
💡Pounds per cubic foot
💡Foot-pounds
Highlights
The video demonstrates how to calculate the work required to pump water over the sides of a swimming pool.
A circular swimming pool with a diameter of 24 feet, sides 5 feet high, and a water depth of 4 feet is considered.
The weight of water is given as 62.5 pounds per cubic foot, which is crucial for calculating work.
The concept of work as Force Times distance is introduced for calculating the work done on a water slice.
A methodical approach of breaking down the problem into slices (or segments) of the pool is presented.
The volume of a water slice is calculated using the formula πr^2Δx, where r is the radius and Δx is the slice thickness.
The force exerted on a water slice is determined by multiplying the volume by the weight of water per cubic foot.
The work done on a single slice is expressed as the force times the distance from the top of the pool to the slice.
An integral is used to sum the work done on all slices to find the total work required to pump the water.
The integration constant, 9000π, is factored out to simplify the calculation.
The limits of integration are set from the top of the water to the top of the pool, and from the water's surface to the pool's base.
The integral is solved to find the total work, resulting in an expression involving x squared from 1 to 5.
The final calculation of work is presented as 108,000π foot-pounds.
The video mentions the applicability of the method to other substances, given their weight per unit volume.
A comparison is made to a previous video on pumping water out of an inverted cone, highlighting the versatility of the method.
The importance of unit consistency in calculations, whether in feet and pounds or meters and kilograms, is emphasized.
The video concludes with an invitation to like, share, subscribe, and explore more calculus integrals in the playlist.
Transcripts
Browse More Related Video
Calculating Work, pumping water out of a circular swimming pool

Work Done Raising a Leaky Bucket with an Integral
Finding Work using Calculus - The Cable/Rope Problem - Part b
Pumping water out of a spherical tank, calculating work, calculus 2 tutorial
Calculate Work to Pump Liquid Out of Tanks - Calculus 2
Pumping water out of a bucket, calculating work, calculus 2 tutorial
5.0 / 5 (0 votes)
Thanks for rating: