Calculating Work, pumping water out of a circular swimming pool

blackpenredpen
25 Apr 201507:27
EducationalLearning
32 Likes 10 Comments

TLDRThis video script demonstrates the calculation of work required to pump water from a circular swimming pool. With a diameter of 24 feet and a water level at 4 feet, the process involves visualizing the pool in horizontal slices, calculating the volume and weight of each slice, and determining the work by integrating the force times distance formula. The strategy uses the density of water and geometric principles to find the total work in foot-pounds, resulting in an answer of approximately 339,292.7 foot-pounds.

Takeaways
  • πŸŠβ€β™‚οΈ The task involves calculating the work needed to pump water from a circular swimming pool.
  • πŸ“ The pool has a diameter of 24 feet and a height of 5T, with the water level at 4T.
  • πŸ”„ Work is calculated by multiplying force by distance, and force can often be found by determining the weight of the object.
  • πŸ’§ The strategy involves visualizing the pool as a series of horizontal slices, each a disc shape, to find the weight of the water.
  • πŸ”’ The volume of each slice is calculated using the formula for the volume of a cylinder: Ο€r^2 * Dy, where r is the radius and Dy is the small change in height.
  • πŸ“ The radius of the pool is constant at 12 feet, simplifying the calculation of the volume for each slice.
  • πŸŒ€ The density of water is given as 62.5 pounds per cubic foot, which is used to find the weight of each water slice.
  • 🚰 The distance each slice must travel to be pumped out of the pool is calculated based on its vertical position, represented as (5 - y).
  • πŸ”„ The work for each slice is the product of the force (weight) and the distance, which is then integrated over the entire water height.
  • ∫ The integral is set up to sum the work for all slices from the bottom (y = 0) to the top (y = 4T) of the water.
  • πŸ“Š After calculating the integral, the total work required to pump the water is found to be approximately 339,292.7 foot-pounds.
Q & A

  • What is the main objective of the script?

    -The main objective of the script is to calculate the work required to pump water out of a circular swimming pool.

  • What is the diameter of the swimming pool mentioned in the script?

    -The diameter of the swimming pool is 24 feet.

  • What is the height of the swimming pool and the current water level?

    -The height of the swimming pool is 5T (presumably 5 times a certain unit, likely feet), and the current water level is 4T.

  • What is the strategy for calculating the work in this scenario?

    -The strategy involves calculating the force required to move the water, which is found by determining the weight of the water, and then multiplying by the distance the water needs to be moved.

  • How is the weight of the water determined in the script?

    -The weight of the water is determined by calculating the volume of a horizontal slice (disk) of the water, multiplying it by the density of water, and then considering the units used (feet and pounds).

  • What is the formula used to calculate the volume of a horizontal slice of water?

    -The formula used is the area of a circle (Ο€ * r^2) multiplied by the thickness of the slice (Dy), where r is the radius of the pool.

  • What is the density of water used in the calculations?

    -The density of water used in the calculations is 62.5 pounds per cubic foot.

  • How is the distance the water needs to be moved determined?

    -The distance is determined by considering the height above the water level at which the water needs to be pumped, which is calculated as 5 minus y, where y is the vertical position of the disk.

  • What mathematical method is used to calculate the total work required?

    -The method used is integration, which sums up the work required for each small disk of water from the bottom to the top of the pool.

  • What are the units of the final answer for the work required?

    -The units of the final answer are foot-pounds, representing the product of force (in pounds) and distance (in feet).

  • What is the numerical result of the integral if calculated correctly?

    -The numerical result of the integral, if calculated correctly, is approximately 339,292.7 foot-pounds.

Outlines
00:00
πŸ’§ Pumping Water from a Swimming Pool

In this section, we calculate the work required to pump water from a swimming pool. The pool has a diameter of 24 feet and a height of 5 feet, with the water level currently at 4 feet. To determine the work, we need to find the force (the weight of the water) and the distance it needs to be moved. By visualizing the pool as a series of horizontal slices, we see that each slice is a disc. The volume of each disc is determined using the formula for the area of a circle (Ο€rΒ²) multiplied by the thickness (dy). With the pool's diameter constant at 24 feet, the radius is always 12 feet. Multiplying the volume by the water's weight density (62.5 pounds per cubic foot) gives us the weight of each slice. The challenge is then to integrate this across the height of the pool.

05:02
πŸ“ Calculating the Distance and Work

We focus on the distance each water slice needs to travel to be pumped out of the pool. With the pool's height at 5 feet and using the y-axis for reference, the distance each slice must travel is (5 - y) feet, where y is the slice's height above the x-axis. To calculate the total work, we multiply this distance by the force (weight) of each slice. Integrating this from the bottom (y = 0) to the water level (y = 4) provides the total work required. The final integral gives us 108,000Ο€, which equals approximately 339,292.7 foot-pounds, with foot-pounds as the unit representing the work done to pump the water out of the pool.

Mindmap
Keywords
πŸ’‘Work
In the context of the video, 'work' refers to the effort required to move an object, in this case, water, against gravity. It is a central concept in physics and is calculated as the product of force and distance. The video demonstrates how to calculate the work needed to pump water out of a swimming pool by considering the force exerted due to the weight of the water and the distance it must be moved.
πŸ’‘Force
'Force' is a push or pull upon an object resulting from its interactions with another object. In the video, the force is primarily the weight of the water, which is the product of mass and gravity. The script explains that understanding the force is essential for calculating the work required to pump water out of the pool.
πŸ’‘Distance
The 'distance' in the video is the vertical height the water must be pumped to clear the pool. It is one of the factors in the work equation, alongside force. The script mentions the importance of calculating the distance the water must travel to determine the total work done.
πŸ’‘Density
'Density' is defined as mass per unit volume and is crucial in the script for determining the weight of a volume of water. The video uses the density of water (62.5 pounds per cubic foot) to calculate the weight of each horizontal slice of water in the pool.
πŸ’‘Volume
The 'volume' of the water slices is calculated in the script by considering the area of the circular base (Ο€r^2) and multiplying it by the height (dy) of each slice. This calculation is essential for determining the weight of the water in each slice and, subsequently, the work required to pump it.
πŸ’‘Cylinder
In the script, the swimming pool is likened to a 'cylinder' for the purpose of calculating the volume of water. The concept of a cylinder is used to describe the shape of the pool and to facilitate the calculation of the volume of water in horizontal slices.
πŸ’‘Horizontal Slices
'Horizontal slices' are imaginary discs cut through the cylindrical pool to calculate the volume and weight of the water in each section. The script describes this method as a way to break down the problem into manageable parts for integration.
πŸ’‘Integration
'Integration' is a mathematical process used in the script to sum up the work required for all the small slices of water in the pool. It is the method by which the total work is calculated by adding up the work for each infinitesimally small slice from the bottom to the top of the pool.
πŸ’‘Pi (Ο€)
'Pi' is a mathematical constant approximately equal to 3.14159, used in the script to calculate the area of the circular base of the water slices. It is a fundamental aspect of the volume calculation for cylindrical shapes.
πŸ’‘Foot Pound
'Foot pound' is the unit of measurement for work in the imperial system, as mentioned in the script. It is the product of force (in pounds) and distance (in feet), and it is the unit used to express the total work required to pump the water out of the pool.
Highlights

Calculating the work required to pump water from a swimming pool involves force times distance.

The force needed is often the weight of the object, such as water in this case.

A visual approach is used by drawing and analyzing the pool's shape and structure.

Horizontal slices of the pool are considered, revealing a disc shape for each slice.

The weight of each water slice is found by calculating its volume and multiplying by water's density.

Water density is given as 62.5 pounds per cubic foot.

The volume of each disc-shaped slice is calculated using the formula for the area of a circle times the slice height.

The radius of the pool, and thus each disc, is half the diameter, which is 12 feet.

The integral calculus method is used to sum up the work for all the discs from the bottom to the top of the pool.

The distance each disc must travel to be pumped out is calculated based on its position within the pool.

The work done to pump each disc is the product of the force (weight) and the distance traveled.

The integral is set up with the lower limit at the pool's bottom (y=0) and the upper limit at the water level (y=4).

The final work calculation integrates the formula for each disc's work from the bottom to the top of the pool.

The result of the integral gives the total work required to pump all the water, approximately 108,000Ο€ foot-pounds.

If Ο€ is not multiplied, the answer is simply 108,000; if Ο€ is included, the result is approximately 339,292.7.

The units for the work done are foot-pounds, combining distance in feet and weight in pounds.

Transcripts

Browse More Related Video

Calculus Work Pump Water From a Circular Swimming Pool

Calculating Work, pumping water out of a tank, calculus 2 tutorial, application of integration

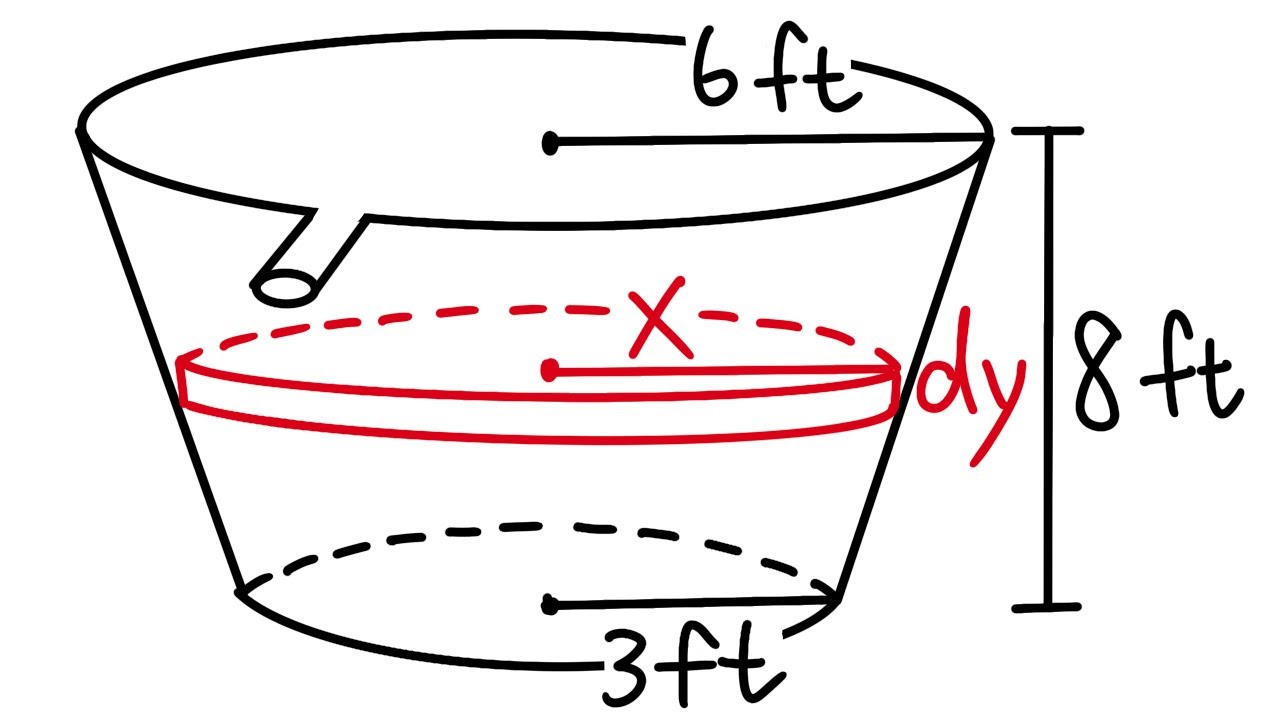
Pumping water out of a bucket, calculating work, calculus 2 tutorial

Work Done Raising a Leaky Bucket with an Integral

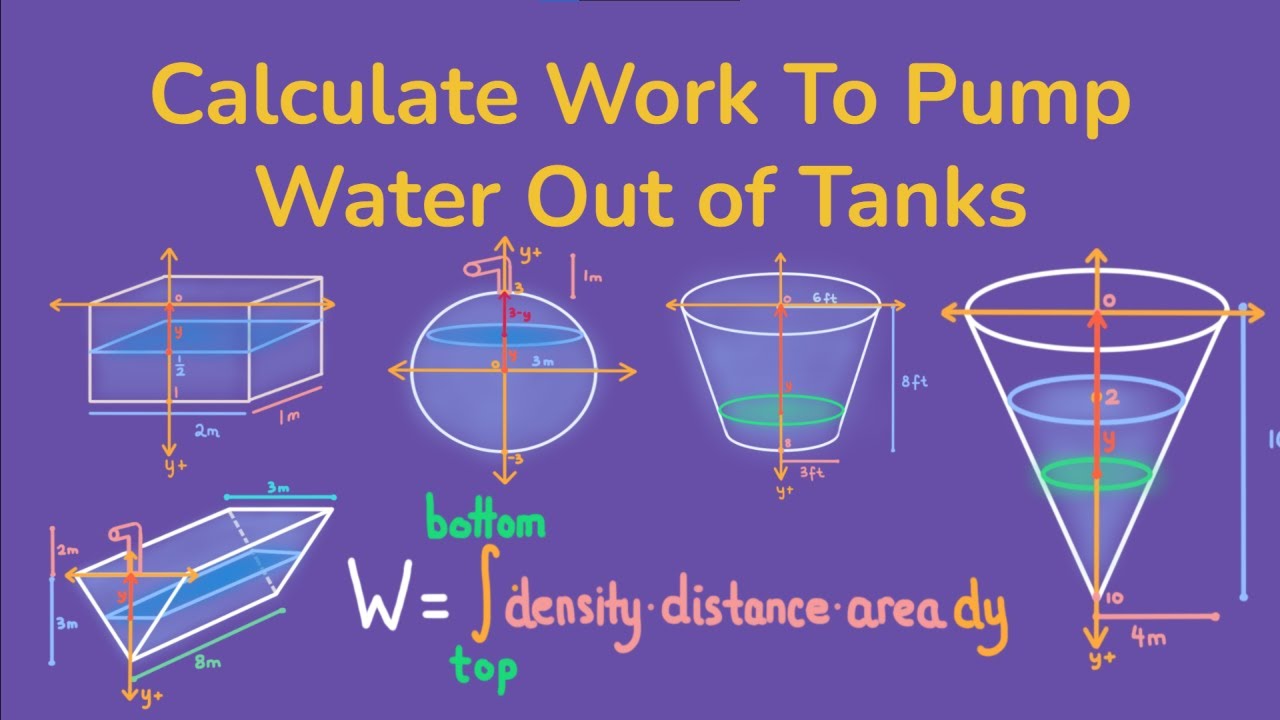
Calculate Work to Pump Liquid Out of Tanks - Calculus 2

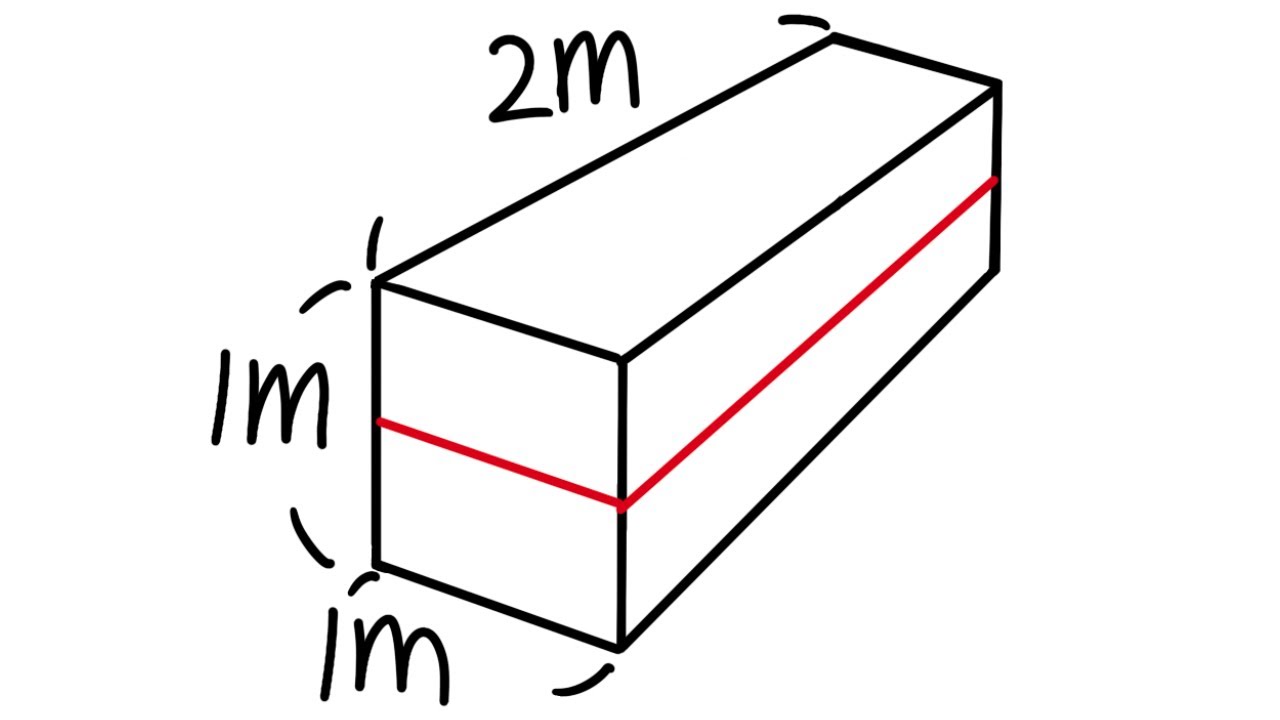
calculating work, pumping water out of a rectangular tank, calculus 2 tutorial

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics CalculationWater PumpingForce DistanceCylinder VolumeDensity WeightHorizontal SlicesIntegration MethodWork FormulaFluid MechanicsEngineering MathEducational Content