Ch. 9.1 Vectors in Two Dimensions
TLDRThis educational video script delves into the fundamentals of vectors, emphasizing their importance in physics and mathematics. It covers vector properties like magnitude and direction, introduces notations, and explains operations such as scaling and vector addition through geometric methods like the parallelogram rule and tip-to-tail method. The script also explores vector representation in component form, standard unit vectors, and their applications in modeling real-world scenarios like force and velocity. It concludes with a practical example of solving for tensions in a system using vector equations.
Takeaways
- 📚 Chapter Nine introduces vectors, emphasizing their importance in physics and mathematics, particularly in classical mechanics and linear algebra.
- 📏 Vectors are characterized by two main properties: magnitude (length) and direction, which are fundamental in describing physical phenomena.
- 🧭 The direction of a vector is as crucial as its magnitude; both determine the vector's identity, regardless of its position in space.
- 🔍 Vectors can be graphically represented, and their operations, such as scaling and addition, can be visualized and understood through geometric methods.
- ⚖️ The parallelogram method and the tip-to-tail method are two geometric approaches to adding vectors, each creating a different visual representation of the resultant vector.
- ✖️ Subtracting vectors can be conceptualized as adding a vector with a negative scalar, effectively reversing its direction while maintaining its magnitude.
- 📈 The component form of a vector is discussed in terms of its x and y components, derived from the differences in coordinates between two points.
- 📐 The magnitude of a vector can be calculated using the Pythagorean theorem, relating the vector's components to its length.
- 🔢 Vector operations can also be performed algebraically, such as adding vectors component-wise or multiplying a vector by a scalar.
- 🎮 Vectors are applied in real-world scenarios like video games, where force and velocity vectors dictate the movement and interactions within the game.
- 📉 The zero vector, composed entirely of zeros, represents a unique case in vector mathematics, often used as an additive identity.
Q & A
What is the primary focus of Chapter Nine in the transcript?
-Chapter Nine focuses on vectors, starting with two-dimensional vectors and moving into three-dimensional vectors, discussing their importance in physics and mathematics.
Why are vectors considered important in physics?
-Vectors are important in physics because they are used extensively to model real physical situations and are fundamental in classical mechanics.
What are the two inherent properties of a vector?
-The two inherent properties of a vector are its length (magnitude) and direction.
How does the length of a vector relate to the force it represents?
-The length of a vector represents the magnitude of the force, with a longer vector indicating a greater force and a shorter vector indicating a lesser force.
What is the graphical representation of a vector?
-Graphically, a vector is represented by an arrow with a specific length and direction, starting from an initial point and ending at a terminal point.
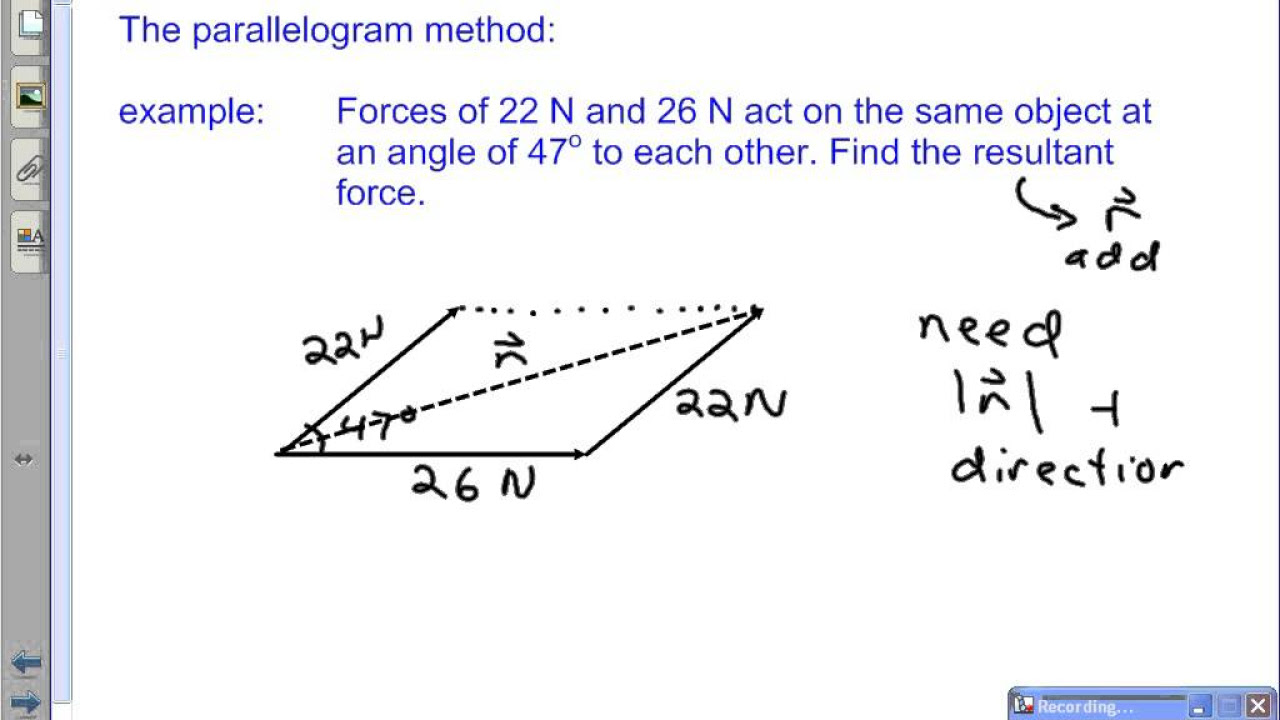
What is the parallelogram method for adding two vectors?
-The parallelogram method involves placing the initial points of two vectors together and drawing the remainder of the parallelogram formed by the vectors, then drawing the diagonal from the connected initial points to find the resultant vector.
What is the tip-to-tail method for adding two vectors?
-The tip-to-tail method involves placing the initial point of one vector at the terminal point of another vector, then drawing a line to connect them, forming a triangle, with the resultant vector being the line that completes the triangle.
How can a vector be scaled by a scalar?
-A vector can be scaled by multiplying each of its components by a scalar value, which can make the vector longer or shorter while maintaining its direction, or even reverse its direction if the scalar is negative.
What is the component form of a vector and how is it derived?
-The component form of a vector is derived from its x and y components, which are the differences in x and y values between the initial and terminal points of the vector.
What is the magnitude of a vector and how is it calculated?
-The magnitude of a vector, also known as the norm, is the length of the vector and is calculated using the Pythagorean theorem by taking the square root of the sum of the squares of its components.
What are the standard unit vectors in two dimensions?
-The standard unit vectors in two dimensions are i and j, which have lengths of one and lie along the x and y axes, respectively.
How can any vector be represented in terms of the standard unit vectors i and j?
-Any vector can be represented as the sum of its x component multiplied by i and its y component multiplied by j, effectively decomposing the vector into its directional components along the x and y axes.
What are the properties of vector addition in the context of R2?
-In R2, vector addition has properties such as commutativity (the order of addition doesn't matter), associativity (grouping of vectors to be added doesn't matter), and the existence of an additive identity (the zero vector).
What is the relationship between the magnitude of a force vector and the amount of force being applied?
-The magnitude of a force vector represents the amount of force being applied, with a larger magnitude indicating a stronger force and a smaller magnitude indicating a weaker force.
How can the tensions in wires holding up a sign be determined using vector equations?
-The tensions in wires can be determined by setting up vector equations based on the forces acting on the sign, including the downward force due to gravity, and solving for the unknown tension magnitudes using the equilibrium condition that the sum of all forces equals zero.
Outlines
📚 Introduction to Vectors
The script begins with an introduction to vectors, emphasizing their importance in various fields, especially physics and mathematics. Vectors are characterized by having both magnitude and direction, which are fundamental in modeling real-world physical situations. The instructor mentions the relevance of vectors in classical mechanics and the existence of a dedicated course on vectors known as linear algebra. The graphical representation of vectors is introduced, along with the concept that vectors maintain their identity regardless of their position in space, as long as their magnitude and direction remain unchanged.
📐 Understanding Vector Properties and Notations
This paragraph delves into the properties of vectors, discussing how they can be scaled by scalar multiplication, which changes their magnitude but not their direction, unless a negative scalar is used, which reverses the direction. The instructor explains two common methods of vector addition: the parallelogram method and the tip-to-tail method, both of which are geometric approaches. The paragraph also covers different notations used to represent vectors in various fields, settling on bold face notation for the course.
🔍 Exploring Vector Addition and Scalar Multiplication
The script continues with an exploration of vector addition, both geometrically and algebraically. The parallelogram rule and the tip-to-tail method are explained with examples. The concept of scalar multiplication is also discussed, illustrating how it affects the magnitude of a vector. The instructor provides a clear example of how to calculate a new vector resulting from the addition of two scaled vectors, emphasizing the importance of understanding both the graphical and algebraic methods of vector operations.
📉 Vector Components and Magnitude Calculation
The discussion shifts to the component form of vectors, explaining how any vector can be broken down into its x and y components. The magnitude (or norm) of a vector is introduced as the length of the vector, calculated using the Pythagorean theorem. The instructor demonstrates how to find the magnitude of a vector given its components and highlights the trigonometric relationship between a vector and its components.
🔄 Vector Operations and Properties in R2
This paragraph covers the operations that can be performed on vectors in a two-dimensional space (R2). The instructor explains the algebraic method of adding vectors component-wise and the scalar multiplication of vectors. Properties such as the commutative and associative properties of vector addition and scalar multiplication are introduced, along with the concepts of additive identity and inverse.
🧭 Vectors in Terms of Unit Vectors and Applications
The script introduces the standard unit vectors i and j, explaining how any vector can be expressed in terms of these unit vectors. The concept of a unit vector is defined as a vector with a magnitude of one. The instructor also touches on the application of vectors in various fields, such as video games, where vectors are used to represent force and velocity in the code.
🏗️ Force and Velocity Vectors in Real-World Applications
The discussion moves to practical applications of vectors, specifically in the context of force and velocity. The instructor uses the example of a sign hanging from a beam with wires to illustrate how vectors can represent the tensions in the wires and the force of gravity acting on the sign. The importance of understanding vector components in analyzing physical systems is emphasized.
📝 Solving Vector Equations with Real-World Examples
The final paragraph demonstrates how to solve vector equations using the example of the sign and wires. The instructor guides through the process of setting up equations based on the horizontal and vertical components of the vectors representing the tensions in the wires and the gravitational force. The solution involves applying trigonometric values and solving for the unknown magnitudes of the tension vectors, showcasing the practical use of vector mathematics in problem-solving.
Mindmap
Keywords
💡Vectors
💡Magnitude
💡Direction
💡Linear Algebra
💡Scalar
💡Component Form
💡Parallelogram Method
💡Tip-to-Tail Method
💡Unit Vectors
💡Force Vectors
💡Velocity Vectors
Highlights
Vectors are fundamental in creating models for real-world physical situations and are extensively used in physics.
An entire course in mathematics, linear algebra, is dedicated to the study of vectors and their properties.
Vectors have two inherent properties: length (magnitude) and direction.
The magnitude of a vector represents the strength of the force or effect it models, such as in the case of force or earthquakes.
Vectors maintain their identity regardless of their position in space, as long as their length and direction remain the same.
Graphical representation of vectors allows for visualizing direction and magnitude.
Different notations are used to represent vectors, such as boldface letters and arrows or dots.
A vector is defined by its initial and terminal points, which determine its direction.
Scalars are real numbers used to scale vectors, changing their magnitude without affecting their direction.
The parallelogram method and tip-to-tail method are two geometric approaches to adding vectors.
Component form of vectors allows for algebraic operations, such as addition and scalar multiplication.
The magnitude of a vector can be calculated using the Pythagorean theorem, relating it to trigonometry.
Vectors can be represented in multiple ways, including component form, i and j notation, and horizontal/vertical components.
Properties of vectors in R2 include commutative, associative, and distributive properties, as well as additive identity and multiplicative identity.
Vectors are used in various fields, including video games, where they represent force and velocity in game physics.
The standard unit vectors i and j are used to express any vector in terms of its components along the x and y axes.
Vectors can be placed with their initial point at the origin for simplicity in analysis and application.
Force and velocity are two primary applications of vectors in classical mechanics, representing the push/pull and speed/direction of objects.
An example problem involving finding tensions in wires holding a sign uses vector equations to solve for unknown magnitudes.
Transcripts
Browse More Related Video

Calculus 3: Vectors (Video #2) | Math with Professor V

Resultant vector | Vector addition: Grade 10 Physics
1-2 C Vector Addition - 2 (Parallelogram Method)

Vectors Full Topic -Physics
Lec 1: Dot product | MIT 18.02 Multivariable Calculus, Fall 2007

03 - Add & Subtract Vectors Using Components, Part 1 (Calculate the Resultant Vector)
5.0 / 5 (0 votes)
Thanks for rating: