1-2 C Vector Addition - 2 (Parallelogram Method)

David Lepischak
27 Feb 201307:42
EducationalLearning
32 Likes 10 Comments

TLDRThis video script explains the parallelogram method for adding two vectors to find the resultant force. Using the example of two forces, 22 and 26 newtons at an angle of 47 degrees, the script illustrates how to draw a diagram with the vectors tail to tail and then tip to tail to form a parallelogram. The cosine law is applied to calculate the magnitude of the resultant force, which is found to be 44.08 newtons. To determine the direction, the sine law is used, resulting in an angle of 21.4 degrees relative to the 26 newton vector. The final answer is presented as a vector with a magnitude of 44.5 newtons (rounded to two decimal places) at an angle of 21.4 degrees to the 26 newton force vector.

Takeaways
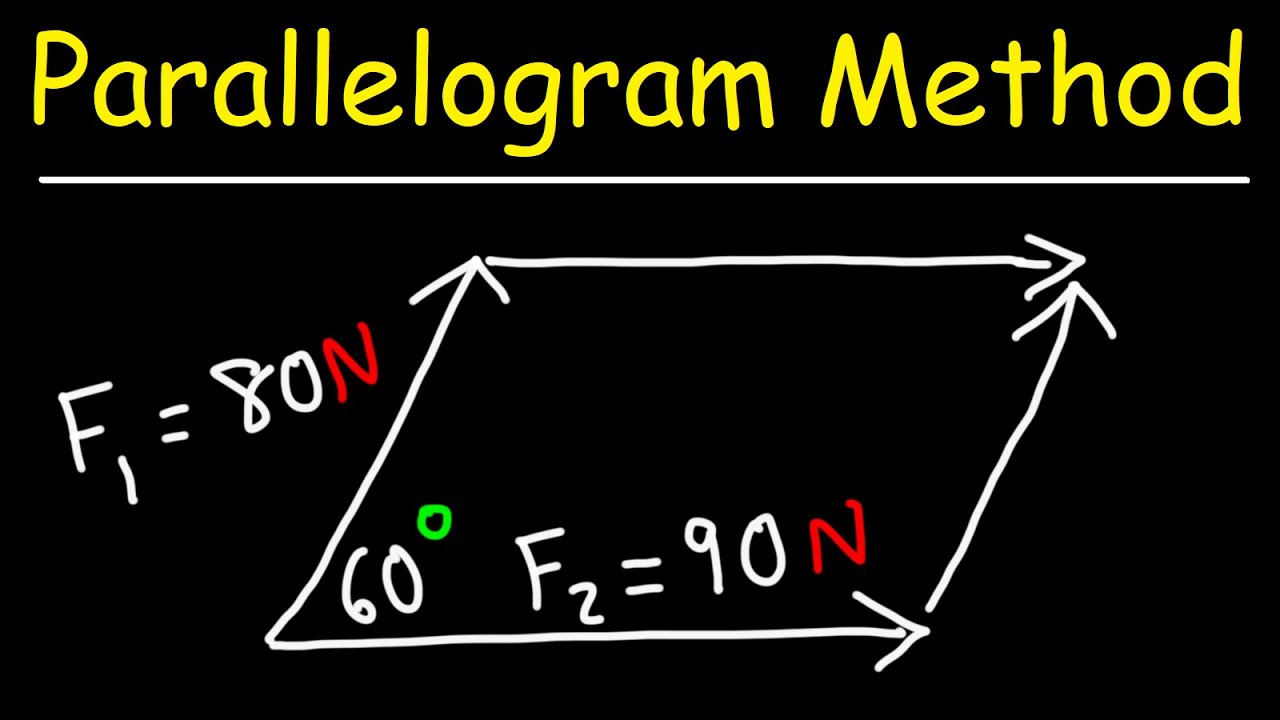
  • ๐Ÿ“ The parallelogram method is used to add two vectors together by placing them tail to tail and drawing a parallelogram to find the resultant vector as the diagonal.
  • ๐Ÿ“ Two forces given in the problem are 22 newtons and 26 newtons, acting on the same object at an angle of 47 degrees to each other.
  • ๐Ÿ“ To find the resultant force, a diagram is drawn with the two forces represented as arrows, tail to tail, to visualize the angle between them.
  • ๐Ÿ”„ The vectors are then repositioned tip to tail to form the parallelogram, with the resultant vector starting from the tail of the 26 newton vector and ending at the tip of the 22 newton vector.
  • ๐Ÿงฎ The cosine law is applied to find the magnitude of the resultant vector (R), using the known sides (22 and 26 newtons) and the angle (133 degrees) between them.
  • โœ… The magnitude of the resultant vector (R) is calculated to be 44.08 newtons, with an emphasis on maintaining precision for intermediate steps.
  • ๐Ÿ”ข To determine the direction of the resultant vector, the sine law is used, with the known magnitude of R and the angle of 133 degrees.
  • ๐Ÿ“ The angle theta, which is the direction of the resultant vector relative to the 26 newton vector, is found using the sine law and is calculated to be 21.4 degrees.
  • ๐ŸŽฏ The final resultant force is specified by its magnitude and direction, given as 44.5 newtons (rounded to two decimal places) at an angle of 21.4 degrees relative to the 26 newton vector.
  • ๐Ÿ“ It's important to keep track of the decimal places during calculations, and the final answer is rounded to two decimal places for practical purposes.
  • ๐Ÿ“ˆ The process demonstrates the application of trigonometric laws (cosine and sine) in physics to solve for the magnitude and direction of a resultant force from two given vectors.
Q & A

  • What is the parallelogram method used for in the context of the script?

    -The parallelogram method is used to add two vectors together to find the resultant force when they act on the same object at a specific angle to each other.

  • What are the two forces given in the script?

    -The two forces given in the script are 22 newtons and 26 newtons.

  • What is the angle between the two forces?

    -The angle between the two forces is 47 degrees.

  • Why do we place the vectors tail to tail when we know the angle between them?

    -We place the vectors tail to tail to visualize the angle between them accurately and to prepare for the next step of placing them tip to tail for vector addition.

  • How is the resultant vector represented in the parallelogram method?

    -In the parallelogram method, the resultant vector is represented as the diagonal of the parallelogram formed by the two vectors placed tip to tail.

  • What laws are used to find the magnitude and direction of the resultant force?

    -The cosine law is used to find the magnitude of the resultant force, and the sine law is used to find its direction.

  • What is the magnitude of the resultant force calculated to be?

    -The magnitude of the resultant force is calculated to be 44.08 newtons.

  • How is the direction of the resultant force determined?

    -The direction of the resultant force is determined by finding the angle (theta) between the resultant vector and one of the original vectors, in this case, the 26 newton vector.

  • What is the direction of the resultant force relative to the 26 newton vector?

    -The direction of the resultant force is 21.4 degrees relative to the 26 newton vector.

  • Why is it important to keep more decimal places in intermediate steps of a calculation?

    -Keeping more decimal places in intermediate steps ensures greater accuracy in the final result, as rounding errors can accumulate and affect the precision of the outcome.

  • What is the final expression for the resultant force in terms of magnitude and direction?

    -The final expression for the resultant force is 44.5 newtons at an angle of 21.4 degrees to the 26 newton vector, with the magnitude rounded to two decimal places.

  • Why is it necessary to specify the angle of the resultant force relative to one of the original vectors?

    -Specifying the angle relative to one of the original vectors provides a clear reference for the direction of the resultant force, making it easier to understand and visualize in the context of the problem.

Outlines
00:00
๐Ÿ“ Applying the Parallelogram Method to Add Vectors

This paragraph introduces the parallelogram method for adding two vectors, specifically forces in this case. The scenario involves adding a 22 Newton force and a 26 Newton force that act on the same object at an angle of 47 degrees. The objective is to find the resultant force. The explanation includes drawing a diagram with the vectors tail to tail and then repositioning them tip to tail to form a parallelogram. The resultant vector is depicted as the diagonal of this parallelogram. To calculate the magnitude and direction of the resultant force 'r', the cosine law is applied using the known side lengths and the angle between them, which is found by subtracting the given angle from 180 degrees. The cosine law calculation is not detailed but results in a magnitude of 44.08 Newtons for the resultant force.

05:00
๐Ÿงฎ Finding the Direction of the Resultant Force

Following the calculation of the magnitude of the resultant force, this paragraph focuses on determining its direction. The direction is defined relative to one of the original vectors, in this case, the 26 Newton vector. The angle theta between the resultant force and the 26 Newton vector is found using the sine law. The known values include the magnitude of the resultant force, the length of one side of the triangle formed by the forces, and the sine of the angle opposite that side. By setting up the sine law equation and solving for theta, the angle is found to be 21.4 degrees. The final step is to combine the magnitude and direction to fully specify the resultant force vector, which is stated as 44.5 Newtons at an angle of 21.4 degrees relative to the 26 Newton vector.

Mindmap
Keywords
๐Ÿ’กParallelogram Method
The parallelogram method is a graphical technique used to add two vectors together. In the video, it is used to find the resultant force of two forces acting on the same object. The method involves placing the vectors tail to tail and then creating a parallelogram by extending one vector to form a diagonal, which represents the resultant vector. This method is central to the video's demonstration of vector addition.
๐Ÿ’กVectors
Vectors are quantities that have both magnitude and direction. In the context of the video, forces are treated as vectors, with the magnitude representing the strength of the force and the direction indicating the line along which the force acts. The video involves adding two vector forces to find their resultant force, which is a fundamental concept in physics.
๐Ÿ’กForce
Force is a physical quantity that represents the interaction causing a change in the motion of an object. In the video, two forces of 22 and 26 newtons are mentioned, which are the magnitudes of the vectors being added together. The concept of force is integral to understanding the problem of finding the resultant force acting on an object.
๐Ÿ’กResultant Force
The resultant force is the single force that represents the combined effect of all the forces acting on an object. In the video, the goal is to calculate this force by adding the two given forces using the parallelogram method. The resultant force is key to understanding the final output of the vector addition process.
๐Ÿ’กAngle
The angle is a measure of the space between two lines or vectors in two-dimensional space. In the video, the angle between the two forces is given as 47 degrees, which is crucial for setting up the parallelogram and applying the cosine law to find the magnitude of the resultant force.
๐Ÿ’กCosine Law
The cosine law is a formula used in geometry to find a side length of a triangle when the lengths of the other two sides and the size of the included angle are known. In the video, it is used to calculate the magnitude of the resultant force by considering the triangle formed by the two forces and the resultant.
๐Ÿ’กSine Law
The sine law is another fundamental principle in trigonometry that relates the lengths of the sides of a triangle to the sines of its angles. In the video, the sine law is applied to find the direction of the resultant force by solving for the angle between the resultant and one of the original forces.
๐Ÿ’กMagnitude
The magnitude of a vector is its length or the size of the vector, which corresponds to the strength of the force in the context of the video. The magnitude is calculated using the cosine law and is an essential component in determining the resultant force.
๐Ÿ’กDirection
The direction of a vector is the angle it makes with a reference line. In the video, finding the direction of the resultant force is as important as finding its magnitude. The direction is determined using the sine law and is measured relative to one of the original forces.
๐Ÿ’กNewtons
Newtons is the unit of measurement for force in the International System of Units (SI). In the video, forces are expressed in newtons, which helps in quantifying the magnitude of the forces being added together.
๐Ÿ’กTriangle
In the context of the video, a triangle is formed by the two forces and their resultant when placed tip to tail. This triangle is used to apply the cosine law and sine law to find the magnitude and direction of the resultant force. The triangle serves as a geometric representation of the vector addition problem.
Highlights

Using the parallelogram method to add two vectors together

Given two forces of 22 and 26 newtons acting on the same object at an angle of 47 degrees

Need to find the resultant force by adding the two vectors

Draw a diagram illustrating the two forces tail to tail

Move the 22 newton vector so it is tip to tail with the 26 newton vector to form a parallelogram

The resultant vector is the diagonal of the parallelogram

Use sine law and cosine law to find the magnitude and direction of the resultant vector

Use cosine law with the 26 and 22 newton vectors and angle 133 degrees to find magnitude of resultant

Magnitude of resultant is 44.08 newtons

Use sine law with the 22 newton vector, angle 133 degrees, and resultant magnitude to find angle theta

Angle theta is 21.4 degrees

Specify the direction of the resultant vector as 21.4 degrees relative to the 26 newton vector

Resultant force is 44.5 newtons at an angle of 21.4 degrees to the 26 newton vector

Round magnitude to two decimal places for final answer

Demonstrates the step-by-step process of using the parallelogram method to add vectors and find resultant force

Clear explanation and visuals make it easy to understand the method

Provides a practical example of applying vector addition in physics problems

Uses trigonometric laws (sine and cosine) to calculate magnitude and direction

Highlights the importance of drawing a diagram and visualizing the vectors

Shows how to move vectors from tail to tail to tip to tail for addition

Provides the final answer with magnitude and direction specified

Transcripts

Browse More Related Video

AP Physics B Kinematics Presentation General Problems #07

Calculating the Resultant force Using Parallelogram Law, แˆˆแŠขแ‰ตแ‹ฎแŒตแ‹ซแ‹แ‹ซแŠ•

4 Resultant force of two vectors at different angles

How To Use The Parallelogram Method To Find The Resultant Vector

Lesson 6 - Finding The Resultant Of Two Forces, Part 2 (Engineering Mechanics Statics)

AP Physics B Kinematics Presentation #51

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Vector AdditionParallelogram MethodForce CalculationPhysics TutorialCosine LawSine LawResultant ForceMathematical PhysicsEducational ContentEngineering MechanicsProblem Solving