03 - Add & Subtract Vectors Using Components, Part 1 (Calculate the Resultant Vector)

This paragraph introduces the concept of adding and subtracting vectors using their components. It emphasizes the importance of this skill in physics, as vectors are used to represent forces, velocities, and other physical quantities. The lesson explains that instead of using graphical methods, which can be cumbersome, the component method is more efficient and reliable. The process of breaking down a vector into its X and Y components is described, and the rule for adding vectors is straightforward: add the X components together to get the X component of the resultant vector, and do the same for the Y components.

This paragraph compares the graphical method of vector addition with the component method. It explains that while graphical methods provide an intuitive understanding, they are not practical for solving complex problems. The component method, on the other hand, allows for easy addition of vectors by simply adding their respective X and Y components. The paragraph provides a step-by-step guide on how to perform vector addition using the component method, including how to find the resultant vector's X and Y components and how to visualize the process.

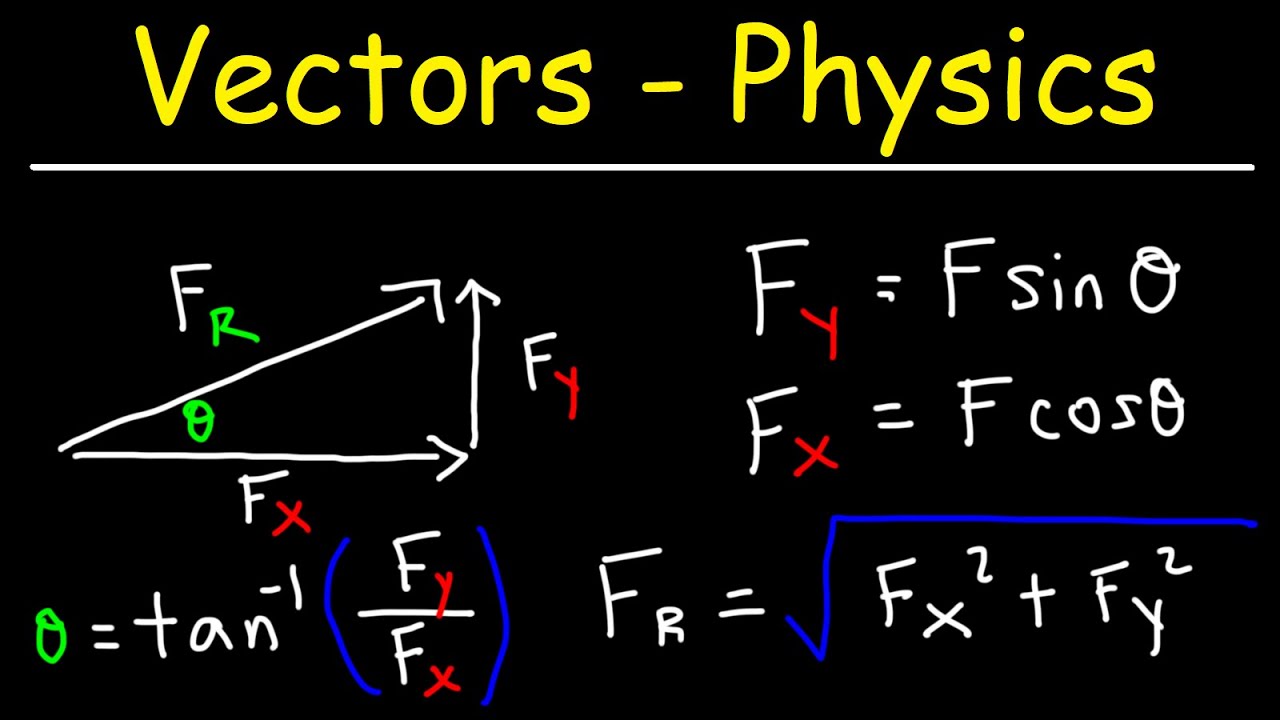
This paragraph delves into the process of finding the magnitude and direction of the resultant vector after addition. It explains that once the X and Y components of the resultant vector are known, the magnitude can be calculated using the Pythagorean theorem. The angle of the resultant vector can be found using the inverse tangent of the ratio of the Y component to the X component. The paragraph reinforces the idea that vector addition and subtraction can be applied to various physical scenarios, such as forces acting on an object.

This paragraph introduces the concept of vector subtraction, which is analogous to adding a vector with reversed direction. It explains that to subtract one vector from another, one simply reverses the direction of the vector being subtracted and then adds it to the original vector. The process is demonstrated both graphically and using components, showing that the component method is a versatile tool for both addition and subtraction of vectors. The paragraph also emphasizes the importance of visualizing vector operations to ensure the correctness of the results.

This paragraph discusses the conversion between vector representation in components and in magnitude and direction. It explains that while components (X and Y) are useful for performing vector operations, the magnitude and direction are often needed to fully describe a vector's physical significance. The paragraph provides an example of how to convert the components of a resultant vector back into its magnitude and direction using the Pythagorean theorem and inverse tangent function. It also highlights the importance of checking the angle obtained from the calculations against the expected direction based on the vector diagram.

This paragraph summarizes the skills learned in the previous sections and sets the stage for more complex vector problems. It emphasizes that understanding the individual steps of breaking down vectors into components, adding or subtracting them, and converting back to magnitude and direction is crucial for solving comprehensive physics problems. The paragraph encourages the learner to apply these skills in future problems, where they will need to combine them to handle scenarios involving magnitude and direction of vectors.