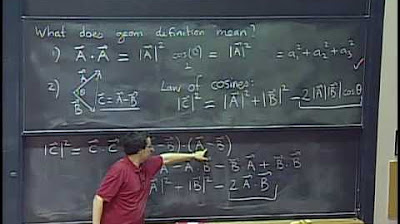Calculus 3: Vectors (Video #2) | Math with Professor V
TLDRThis video script delves into the fundamentals of vectors, distinguishing them from scalars by their directional nature. It covers vector representation, magnitude calculation, and operations like addition, scalar multiplication, and subtraction. The script also introduces unit vectors and their significance, culminating in an applied example of finding tensions in ropes supporting a holiday decoration, demonstrating the practicality of vector concepts in physics.
Takeaways
- 📚 Vectors are quantities with both direction and magnitude, unlike scalars which only have magnitude.
- 📏 Scalars are used for quantities like height or count, which do not require direction, such as 6 feet tall or 4 jellybeans.
- 🚀 Vectors are used for quantities that include direction, such as velocity (speed and direction, e.g., 50 mph north).
- 🔍 Vectors can be represented as directed line segments, or arrows, where the length indicates magnitude and the direction is shown by the arrowhead.
- 🌐 Vectors can be relocated without changing their magnitude or direction, often positioned with their initial point at the origin for simplicity.
- 📈 The magnitude of a vector is calculated using the square root of the sum of the squares of its components, like √(a1² + a2²) for 2D vectors.
- 🧭 The zero vector has a magnitude of zero and can be represented as (0, 0) in 2D or (0, 0, 0) in 3D, and it can point in any direction.
- ⚖️ Vector addition can be done geometrically using the triangle rule (tip-to-tail) or the parallelogram rule, and algebraically by adding corresponding components.
- 🔢 Scalar multiplication involves multiplying the vector's components by the scalar, effectively stretching or compressing the vector while maintaining its direction.
- 🔄 Vector subtraction is defined as adding the vector and its opposite, which can be visualized by reversing one vector and adding it to the other.
- 📉 Unit vectors are vectors with a magnitude of 1, and any vector can be converted into a unit vector by dividing its components by its magnitude.
Q & A
What is the fundamental difference between a scalar and a vector?
-A scalar represents a quantity with only magnitude, whereas a vector represents a quantity with both magnitude and direction.
Why would you use a vector to describe the velocity of an object?
-You would use a vector to describe the velocity of an object because it contains both the speed (magnitude) and the direction of the object's movement.
What is a position vector?
-A position vector is a way to represent a vector where the initial point is at the origin, and the vector is described by the coordinates of the terminal point.
How are vectors U and W considered equal in the script?
-Vectors U and W are considered equal if they have the same magnitude, the same length, and the same direction, regardless of their initial positions.
What does the magnitude of a vector represent?
-The magnitude of a vector represents the length or size of the vector, which can be calculated using the square root of the sum of the squares of its components.
What is the zero vector and how is it represented?
-The zero vector is a vector with a magnitude of zero, represented as '0' with a vector symbol above it, or with components (0, 0) in two-dimensional space and (0, 0, 0) in three-dimensional space.
How can you add two vectors geometrically?
-You can add two vectors geometrically using the triangle rule (tip-to-tail) or the parallelogram rule, where the sum of the vectors is represented by the diagonal of the parallelogram formed by the two vectors.
What is scalar multiplication of a vector?
-Scalar multiplication of a vector involves multiplying the vector by a scalar (a real number), which results in a new vector that has the same direction as the original but with a magnitude that is a multiple of the original.
How do you find the unit vector in the direction of a given vector?
-To find the unit vector in the direction of a given vector, you divide each component of the vector by its magnitude.
What is the significance of the special unit vectors î, ĵ, k̂ in vector representation?
-The special unit vectors î, ĵ, k̂ represent the directions of the coordinate axes in three-dimensional space, and they provide an alternate method for representing vectors using components.
How can you solve for the tension in each rope in the given static equilibrium example?
-You can solve for the tension in each rope by setting up a system of equations based on the horizontal and vertical components of the tension vectors and the weight vector, and then solving for the magnitudes of the tension vectors.
Outlines
📚 Introduction to Vectors in Calculus 3
This paragraph introduces the concept of vectors in the context of calculus 3. It explains the difference between scalars, which have only magnitude, and vectors, which have both magnitude and direction. The paragraph provides examples of quantities that can be represented by vectors, such as velocity and force, and contrasts them with scalar quantities like height or volume. It also discusses the representation of vectors as directed line segments or arrows, and the concept of position vectors, which are vectors with an initial point at the origin. The paragraph concludes with an exercise to sketch position vectors and verify their equality, emphasizing the importance of direction and magnitude over the vector's initial position.
📐 Vector Magnitude and Scalar Multiplication
The second paragraph delves into the concept of vector magnitude, which is a precise definition of the length or size of a vector. It explains how to calculate the magnitude of a vector in both two-dimensional and three-dimensional space using the Pythagorean theorem. The paragraph also introduces the zero vector, its properties, and the distinction between the zero vector and the scalar zero. It then covers the geometric and algebraic methods for adding vectors, including the triangle rule and the parallelogram rule, and explains the algebraic verification of vector equality. The section concludes with a discussion on scalar multiplication of vectors, illustrating how to perform this operation both graphically and algebraically.
🔢 Component Form and Vector Operations
This paragraph focuses on the algebraic representation of vectors through their components and the operations that can be performed on them. It explains how to add vectors by simply adding their corresponding components and how scalar multiplication affects the magnitude of a vector while keeping its direction unchanged. The paragraph also discusses the process of finding the magnitude of a scalar multiple of a vector and provides a step-by-step example of how to sketch and express a vector in component form after changing its direction. The concept of parallel vectors is introduced, along with a formal definition and a method to check for parallelism without graphing.
⚖️ Vector Subtraction and Properties
The fourth paragraph explores the concept of vector subtraction, both geometrically and algebraically, and introduces the properties of vectors. It explains how to find the difference between two vectors by adding the first vector and the negative of the second, using both the triangle method and the parallelogram method. The paragraph also discusses the algebraic approach to vector subtraction by subtracting their components. It then lists several important properties of vectors, such as commutativity, associativity, identity, and distributivity, which are fundamental for understanding vector operations. The section concludes with a problem that applies these concepts to find the result of an operation involving vector addition and scalar multiplication.
📏 Unit Vectors and Special Vector Notation
This paragraph introduces the concept of unit vectors, which are vectors with a magnitude of 1, and explains how to find a unit vector in the same direction as a given vector by scaling down its components. It also discusses the special unit vectors î, ĵ, and k̂, which correspond to the directions of the coordinate axes in three-dimensional space, and how they can be used to represent vectors in component form. The paragraph emphasizes the importance of using the correct notation for vectors, especially when distinguishing between vectors and scalars, and provides examples of how to express vectors using both standard and special unit vectors.
🧩 Applications of Vectors: Static Equilibrium
The sixth paragraph presents an application of vectors in the context of static equilibrium, specifically in a physics problem involving a holiday decoration suspended by two ropes of different lengths and angles. The paragraph explains how to set up the problem by drawing a diagram and identifying the forces involved, such as the downward gravitational force and the upward tension forces in the ropes. It then demonstrates how to use vector components to represent the tension forces, taking into account their horizontal and vertical components, and how to apply the conditions of equilibrium to create a system of equations. The paragraph concludes with the solution to the system, finding the magnitude of the tension in each rope and expressing the tension forces as vectors in component form.
🏁 Conclusion and Further Exploration
The final paragraph wraps up the discussion on vectors with a summary of the problem-solving process and an invitation to continue exploring the topic. It emphasizes the importance of understanding the vector components and their role in solving equilibrium problems. The paragraph also highlights the significance of vectors in various applications, particularly in physics, and hints at more exciting vector-related content to come in future lessons.
Mindmap
Keywords
💡Vector
💡Scalar
💡Magnitude
💡Position Vector
💡Zero Vector
💡Scalar Multiplication
💡Vector Addition
💡Unit Vector
💡Component Form
💡Static Equilibrium
Highlights
Introduction to vectors as quantities with both direction and magnitude, distinct from scalars.
Explanation of how vectors are represented by directed line segments or arrows.
Vectors U and W are equal if they have the same magnitude and direction, regardless of their locations.
Concept of position vector where the initial point is at the origin and the vector is described by the coordinates of the terminal point.
Illustration of sketching position vectors and verifying vector equality through graphical representation.
Definition and calculation of the magnitude of a vector in both 2D and 3D spaces.
Introduction of the zero vector and its unique properties, including having zero magnitude and representing all directions.
Differentiation between the zero vector and the scalar zero, emphasizing the importance of vector notation.
Geometric methods of vector addition: the triangle rule and the parallelogram rule.
Algebraic method of vector addition by adding corresponding components of the vectors.
Multiplication of vectors by scalars and the effect on the magnitude and direction of the vector.
Scalar multiplication of vectors in component form and its algebraic representation.
Properties of vectors, including commutativity, associativity, identity, and distributive properties.
Application of vector operations to find the tension in ropes holding a holiday decoration in static equilibrium.
Use of trigonometric functions to resolve the tension vectors into horizontal and vertical components.
Solution of a system of equations to find the magnitude of tensions in the ropes.
Conversion of the magnitude of tensions into vector form using their respective angles.
Final answer presentation with the tensions in each rope and their vector components.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: